海森伯格XY模型的负值度

刘思平

(襄樊学院 物理与电子工程学院, 湖北 襄樊 441053)

海森伯格XY模型的负值度

刘思平

(襄樊学院 物理与电子工程学院, 湖北 襄樊 441053)

利用一种通用量子纠缠度——负值度(Negativity)，研究热平衡时在外加磁场(沿z轴)下两量子比特海森伯格XY模型的热纠缠. 当各向异性系数γ足够大时，出现纠缠复苏现象，而且对于一有限温度，可以调节外加磁场来产生纠缠. 而对各向同性，当温度比临界温度高时，负值度为零，与外加磁场无关.

量子纠缠；海森伯格模型；负值度；热纠缠；

量子纠缠现象是量子理论最重要的特性之一，是能够实现经典信息不可能实现的新功能的源泉. 量子信息学直接推动了纠缠态理论的发展. 纠缠态在量子态传输[1]、密钥分配[2]等方面都起着关键的作用. 对纠缠定量的描述即纠缠态的度量是一个复杂而困难的问题，也是量子信息理论中一个重要的课题. 现在关于两粒子系统纯态纠缠理论已经相当完善[3]. 为了度量两体混合态的纠缠，文献[4-5]提出了多种纠缠度，其中负值度(Negativity)[6]是一种好的纠缠度量，对两体混合态可以很方便的计算其纠缠. 纠缠的潜在应用价值激励着人们去研究和控制它，除温度以外，外加磁场是控制纠缠的另一参数. 在热平衡下，由系统的哈密顿量H描述的态为ρ(T )= exp (− H/ k T)/Z ，其中 Z =Tr ⎡⎣exp (− H/ kT )⎤⎦为配分函数，k为玻尔兹曼常数. ρ( T)表示热状态，其纠缠即为热纠缠[7]. 对两量子比特各向同性的海森伯格模型在反铁磁性情况下存在热纠缠，但在铁磁性情况下却不存在热纠缠[8]. 而对各向异性的海森伯格模型，其热纠缠却有不同，如XXZ模型的热纠缠

[9]. 在本文中利用负值度(Negativity)计算了两量子比特各向异性海森伯格 XY模型的热纠缠，研究在热平衡时温度和外加磁场对纠缠的影响. 对各向同性，当温度比临界温度高时，纠缠消失，与外加磁场无关.当各向异性系数足够大时，发生纠缠复苏现象，对一有限温度，可以调节外加磁场来产生纠缠.

1 负值度(Negativity)

由Peres可分离判据[10]，对两体低维2⊗2和2⊗3的系统，其部分转置正定是判定是否为可分离态的充分必要条件，但对于其它情况这只是一个必要的条件. Vidal和Werner根据这一思想提出了一种通用的量子纠缠度量——负值度(Negativity)[6]，对两量子比特来说，其定义为[11-12]：

其中，μmin为ρ的部分转置的最小的本征值. 已经证明对两量子比特可分离态其部分转置只有一个负的本征值.对两体纠缠，负值度可方便的计算其纠缠.

2 XY模型的负值度

两量子比特各向异性Heisenberg XY模型在外加磁场B下(沿z轴)的哈密顿量为：

σi(i = x, y, z )为泡利算符，纠缠密度矩阵：Z为配分函数. J>0表示反铁磁性情况，J<0表示铁磁性情况.为简单化，以下取k=1.

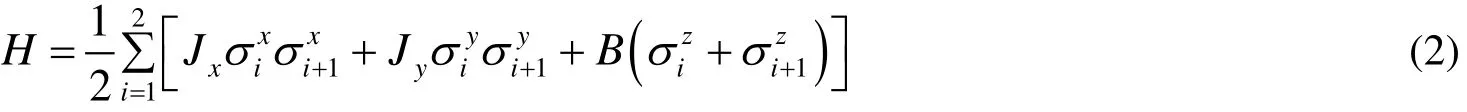
系统的本征态和本征值分别为：

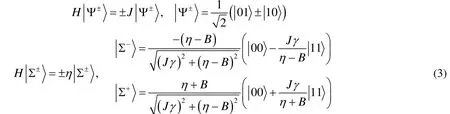
纠缠密度矩阵为:

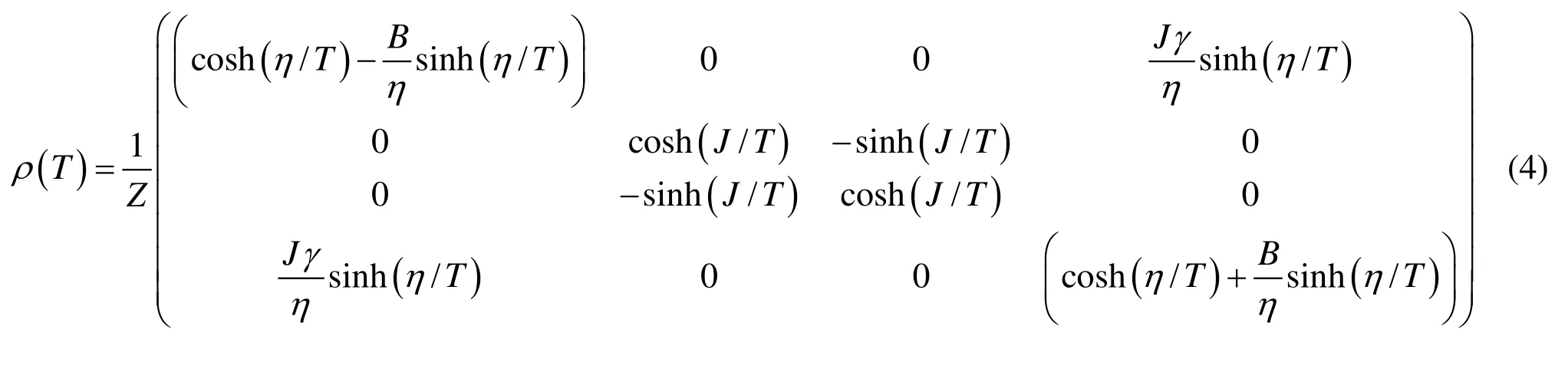
密度矩阵部分转值的本征值为：

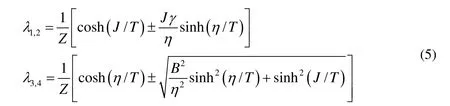
当各向异性系数 γ= 0,0.3,0.6时，利用式(1)画出负值度与温度和磁场的关系图，如图1和图2. 由图可以看出，它们有相似之处，当T=0和B=0时，负值度都为最大值，因为此时，系统为基态，即最大纠缠态Bell态.当γ=0各向同性时，如图1所示，当T=0时，随着磁场的增加，负值度保持一最大值不变即最大纠缠态，当B达到一临界值BC时，负值度迅速减小到零，其中 BC=J=1.实际上，当B>J，基态是非纠缠态，在临界点(T = 0,B = BC= J )发生了量子相变[13].

图1 海森伯格XY模型的负值度与温度和外加磁场的关系( J= 1,γ = 0)

对各向异性的情况，如图2所示，当T=0时，随着B的增加，起初负值度保持一定值等于其最大值，当B达到一临界值BC时，负值度突然下降，这与各向同性的情况相似，所不同的是，当 B>BC时，负值度并不降为零，而且当γ足够大时，负值度由最小值突然增加，经历了一个纠缠复苏过程，如图2(b).

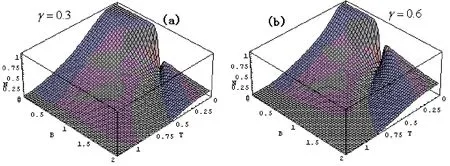
图2 负值度与温度和外加磁场的关系(J=1)

其实 B>BC时，当γ≥0.6都会发生纠缠的复苏，如图3画出负值度与B的关系，对γ=0.3，当 B=BC，负值度急剧下降，当 B>BC，值值度单调下降.对γ≥0.6，当 B=BC，负值度急剧下降但并不降为零，当B>BC，负值度出现了复苏，对γ=0.8同样如此.

从密度矩阵可以看出，当ηJ时，系统的基态为仍为纠缠态，当具有相同的能量，都等于系统的最低能量.一般情况下，当T=0时，系统可表示为态的混合态，其密算符为，对，且当η=J时，，此时有即温度T=0时，量子相变发生在系统为等概率混合的时候.

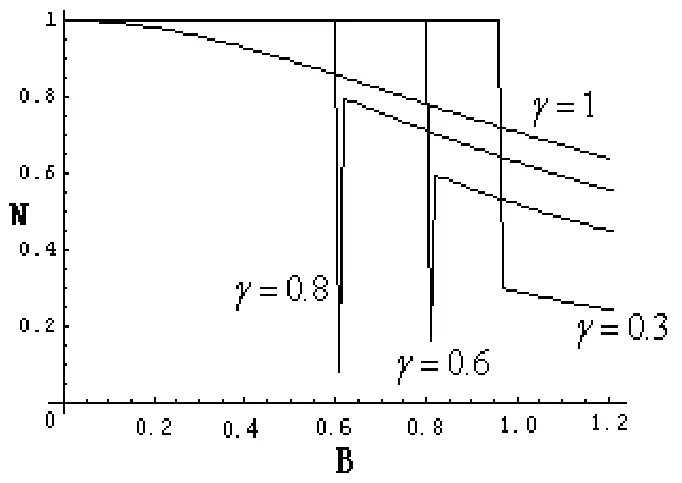
图3 T=0时负值度N与磁场B的关系(J=1)

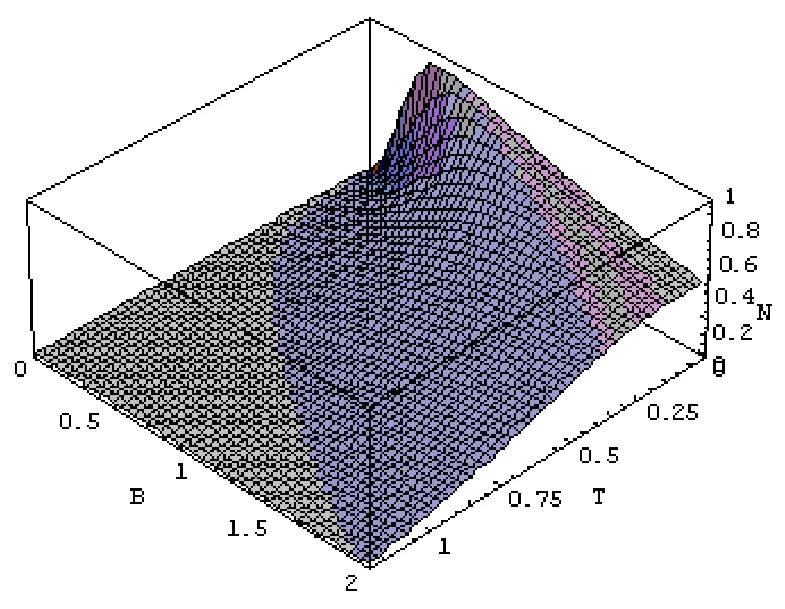
图4 Ising模型的负值度( J= 1,γ = 1)

对Ising模型，即γ=1时，如图4所示，当B=0时，系统负值度为零，即负值度仅由外加磁场决定.由图3可以看出，当T=0时，随着系数γ的增加，量子相变发生点不断减小，当因为对Ising系统，当 B= 0,T = 0时，系统的态为Bell态的等概率混合，其纠缠为零.

3 结语

两量子比特海森伯格XY模型的热纠缠与各向异性系数γ、磁场B和温度T有关. 对各向同性，当温度高于临界温度高，系统没有纠缠，与外加磁场无关，当γ足够大时，存在纠缠复苏现象，而且对于一有限温度，可以调节外加磁场来产生纠缠.

[1] BENNETT C H, BRASSARD G, CREPEAU C, et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolky-Rosen channels[J]. Phys. Rev. Lett., 1993, 70(13): 1895-1899.

[2] DEUTSCH D, EKERT A, JOZSA R, et al. Quantum privacy amplification and the security of quantum cryptography over noisy channels[J. Phys. Rev. Lett., 1996, 77(13): 2818-2821.

[3] 曾谨言, 裴寿镛, 龙桂鲁. 量子力学新进展:第二辑[M]. 北京: 北京大学出版社, 2001: 281.

[4] SCOTT HILL, WOOTTERS WILLIAM K. Entanglement of a pair of quantum bits[J]. Phys. Rev. Lett., 1997, 78: 5022-5025 .

[5] VEDRAL V, PLENIO M B, RIPPIN M A , et al. Quantifying entanglement[J]. Phys. Rev. Lett., 1997, 78: 2275-2279.

[6] VIDAL G, WERNER R F. A computable measure of entanglement[J]. Phys.Rev.A., 2002, 65:032314-032317.

[7] ARNESEN M C, BOSE S, VEDRAL V. Natural Thermal and magnetic Entanglement in 1D Heisenberg Model[J]. Phys. Rev. Lett., 2001, 87: 017901-017904.

[8] 刘思平. 海森伯格XXZ模型的热纠缠[J]. 江汉大学学报: 自然科学版, 2009(3): 33-35.

[9] WANG XIAOGUANG. Effects of anisotropy on thermal entanglement[J]. Physics Letters A, 2001, 281(3): 101-104.

[10] PERES A. Separability criterion for density matrices[J]. Phys.Rev. Lett., 1996, 77: 1413-1415.

[11] ZYCZKOWSKI K, HORODECKI P, SANPERA A, et al. On the volume of the set of mixed entangled states[J]. Phys. Rev. A, 1998, 58: 883-892.

[12] EISERT J, PLENIO M B. A comparison of entanglement measures[J]. J. Mod. Opt., 1999, 46: 145-154.

[13] SACHDEV S. Quantum Phase Transitions[M]. Cambridge: Cambridge University Press, 1999.

（责任编辑：饶 超）

Negativity of Heisenberg XY Model

LIU Si-ping
(Physics and Electronics Information Technology Department, Xiangfan University, Xiangfan 441053, China)

Using a universal entanglement measure, negativity，we investigate the thermal entanglement of two-qubit Heisenberg XY model in thermal equilibrium at temperature T in the presence of an external magnetic field B. When anisotropy parameter γis large enough there occurs a revival of the entanglement. By adjusting the magnetic field B，one can produce entanglement for any finite T. For isotropic case there is no entanglement above a critical temperature that is independent of the external B field.

Entanglement; Heisenberg model; Negativity; Thermal entanglement

O431

A

1009-2854(2010)02-0008-04

2010-01-04

湖北省教育厅科学技术研究计划优秀中青年人才项目(Q20082503)

刘思平(1975— ), 女, 重庆荣昌人, 襄樊学院物理与电子工程学院讲师.