固体火箭发动机延伸喷管折转片接触分析＊

王 锟，蔡体敏

（西北工业大学航天学院，西安 710072）

0 引言

延伸喷管技术是提高固体火箭发动机性能的关键技术之一，也是目前大型先进战略导弹发动机普遍采用的先进技术。由于延伸喷管的组成材料多样，结构比较复杂，而且其展开特性参数（位移、速度及加速度）必须在要求范围内方可正常工作。为保证延伸喷管正常工作，即保障延伸喷管不同材料在工作过程中的应力均在许用应力范围内，有必要对延伸喷管折转片的动态性能进行分析，为延伸喷管研制与改进提供重要的理论依据。目前，有关延伸喷管展开动力学分析方面的资料国外未见报道，国内王成轩、马国宝等人曾用质心运动定律对双节套筒式延伸喷管的展开特性进行了分析，但未考虑各部件转动摩擦力矩及密封圈摩擦力的影响［1－2］。尤军峰等利用实验数据和理论分析对比的方法对延伸锥喷管进行了改进分析［3］，文中重点研究折转片在延伸喷管展开过程中折转片与销轴之间的接触对结构产生的影响。利用ADAMS软件计算了延伸喷管展开过程中折转片支耳处的受力情况，利用其结果将动力接触计算问题简化为静力接触计算问题，并计算了折转片展开到位时的强度和刚度，为延伸喷管折转片改进等提供理论依据。

1 基本理论

1.1 接触有限元方程

在整体坐标系下，两接触物体A和B的有限元方程为：

式中：［KA］、［KB］、｛δA｝、｛δB｝、｛FA｝、｛FB｝、｛RA｝、｛RB｝分别为物体A和B的刚度阵、位移向量、已知节点外力向量及未知接触点力向量。

简写为：

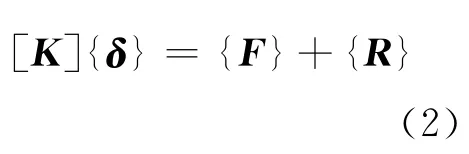
上式即为接触问题有限元方程。

图1 两个接触物体示意图

1.2 三维弹性体接触条件

假定IA、IB在加载前其间隙向量为δ0，加载后其间隙向量为δ1，即两节点分别产生了位移uA、uB而达到新的位置I′A、I′B，关系如下：

将上式写成分量式得：

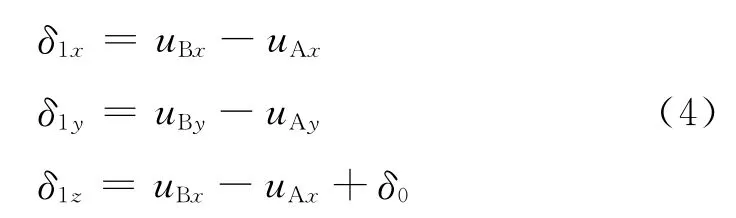
由式（4）和有关力的作用原理及接触状态的四种类型特征，可准确的推导出每种接触节点对的接触条件，如表1所示。

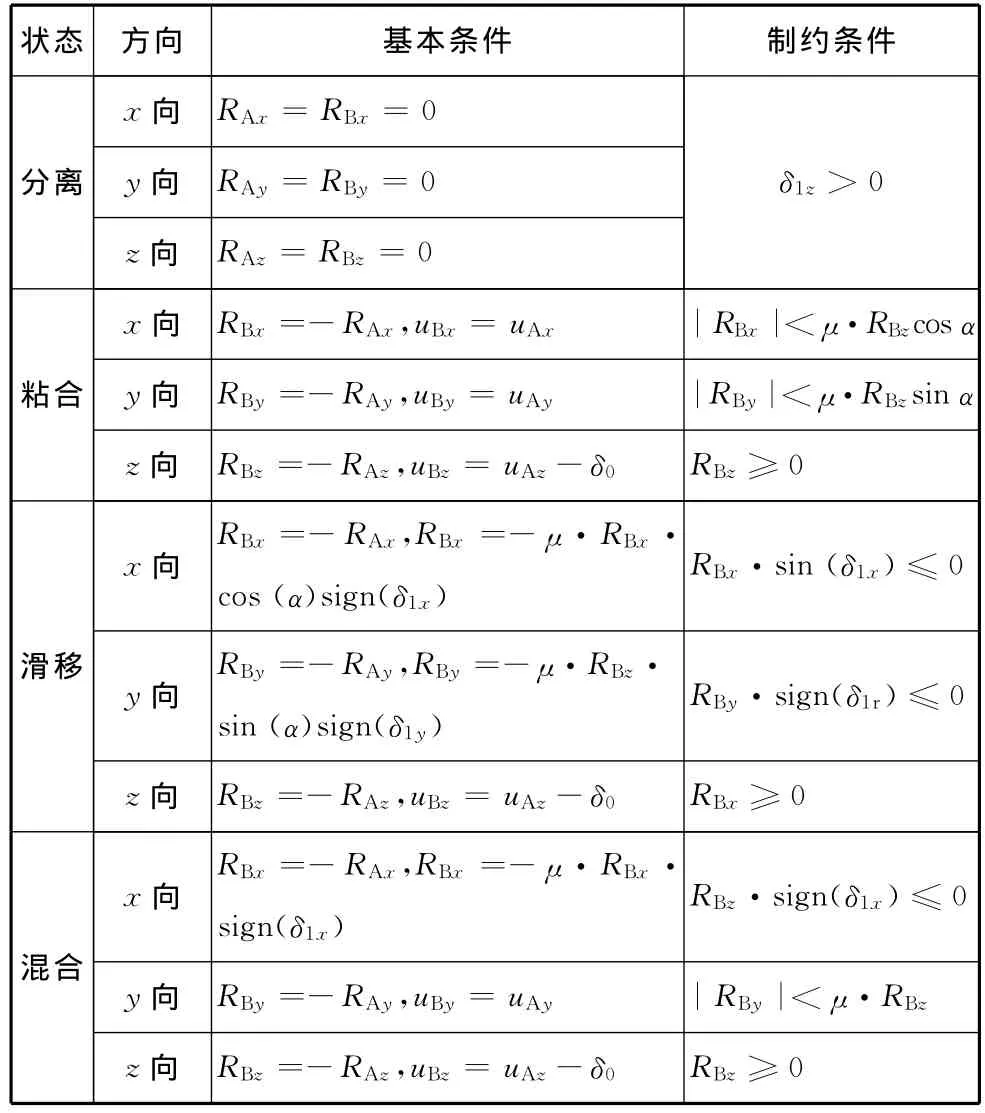
表1 三维弹性接触问题的接触条件

根据求解方程的需要，表1的接触条件分为基本条件和制约条件。基本条件用于补充有限元方程中因接触而产生的未知量，制约条件用于判别有限元解是否满足接触面的物理关系。

1.3 接触摩擦定律

摩擦与接触表面的硬度、湿度、法向应力和相对滑动速度等特性有关，文中采用滑动库仑摩擦模型。库仑摩擦模型是依赖于法向力和相对滑动速度的高度非线性现象，它是速度或位移增量的隐式函数。这种摩擦模型在实际问题中被广泛采用。库仑摩擦模型为：

式中：σn为接触节点法向应力；σfr为切向（摩擦）应力；μ为摩擦系数；t为相对滑动速度方向上的切向单位矢量。

库仑摩擦模型又常常写成节点合力的形式为：

式中ft为剪切力。

实际上经常可以看到当法向力给定后，摩擦力随νr或Δu的值会产生阶梯函数状的变化（如图2所示）。

图2 静摩擦力与滑动摩擦力之间的突变

1.4 接触算法

接触问题属于典型的边界条件非线性问题，采用直接约束法，利用该方法处理接触问题是追踪物体的运动轨迹，一旦探测出发生接触，便将接触所需的运动约束（即法向无相对运动，切线可滑动）和节点力（法向压力和切向摩擦力）作为边界条件直接施加在产生接触的节点上，这种方法对接触的描述精度高，具有普遍适应性，不需要增加特殊的界面单元，也不涉及复杂的接触条件变化，该方法不增加系统自由度数，但由于接触关系的变化会增加系统矩阵带宽。

1.5 接触迭代方程和迭代收敛判别准则

接触问题的有限元求解过程是一迭代过程，对每次迭代可分为两个步骤：对（m＋1）次迭代而言，首先把m次迭代计算出的接触状况Γm、接触力｛R｝m和位移｛δ｝m作为第（m＋1）次迭代的已知条件，利用有限元方程求解，可得（m＋1）次迭代的位移｛δ｝m＋1，由该位移解便可求得（m＋1）次迭代的接触力｛R｝m＋1；其次，利用｛δ｝m＋1和｛R｝m＋1，由制约条件对可能接触面上的全部节点对进行计算，判别其接触类型，即对Γm进行检查、修正，最后得到（m＋1）次迭代的接触状况Γm＋1。如此反复迭代计算，直到满足下列两个收敛准则为止。

1）接触非线性收敛判别准则：两弹性体间的全部接触节点对，其（m＋1）次的接触状态Γm＋1应符合m次的接触状况Γm，即：

2）摩擦非线性收敛判别准则：两弹性体间的全部接触节点对，其（m＋1）次的法向接触力和m次的法向接触力之间的最大相对误差满足一定的精度ε要求，即：

由于每次迭代都要用到前次迭代的计算结果，故在首次迭代时必须给定初值。弹性接触问题有稳定解，通过数次迭代便能逼近正确解。考虑摩擦时，一般通过4～6次迭代可达10－4的计算精度，不计摩擦时，迭代两次即可收敛。

2 计算模型

2.1 有限元模型建立

折转片计算模型建立过程：

1）利用Pro／Engineer软件的几何模型生成二维图，以IGES格式传送至Mentat；

2）利用CHECK／REPAIR GEOMETRY工具进行几何修整；

3）进行平面网格划分，对接触区域的单元进行重点加密；

4）利用mentat的expand功能将平面单元生成三维单元。

生成的有限元模型共15468个单元、21362个节点，如图3所示。

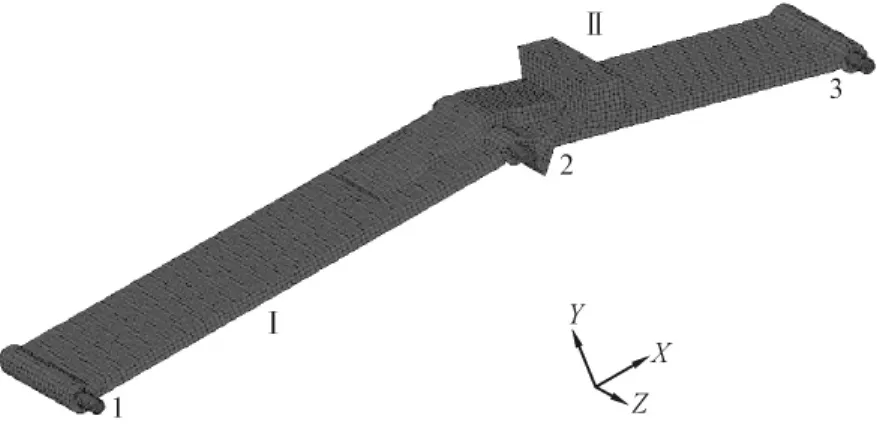
图3 折转片有限元模型

2.2 材料定义

折转片Ⅰ尺寸较长，为抵抗冲击引起的变形问题，材料选为钛合金，折转片Ⅱ材料为铝合金，销轴材料为钢。材料性能如表2所示。

表2 材料参数

2.3 边界条件定义

边界条件参考坐标如图3所示，由于折转片展开到位瞬间的力学性能，因此对销轴1两端固支；销轴2与销轴3两端施加z向（即轴向）约束；折转片Ⅰ与折转片Ⅱ两侧施加z向约束，底部施加y向约束；折转片Ⅱ与延伸锥连接端施加由动力学仿真ADAMS软件计算得 出的反力：x＝ －16056.8095N，y＝20189.0244N。

3 计算结果

利用MARC软件计算折转片的应力如图4和图5所示。

图4 折转片Ⅰ应力云图

图5 折转片Ⅱ应力云图

由计算结果，整个结构最大变形0.052mm，销轴1最大Von Mises应力32.17MPa，销轴2最大Von Mises应力24.38MPa，销轴3最大 Von Mises应力52.91MPa，折转片Ⅰ最大 Von Mises应力59.37MPa，折转片Ⅱ最大Von Mises应力235.7MPa。

4 结论

由计算结果易知，整个结构变形量很小，刚度完全满足要求。各局部结构最大Von Mises也都远小于其材料的许用应力，折转片Ⅱ处应力较高主要由于在该处施加了集中力造成应力偏大，真实值应小于计算值，且计算值仍小于材料的许用应力，因此折转片结构是完全可靠的。该计算分析利用运动和动力学仿真的结果将结构中的动力接触问题简化为静力接触问题进行求解，降低了结构计算的难度和工作量，值得在工程计算分析中借鉴。

［1］王成轩，邹锦术，苏成，等.影响双节套筒式延伸喷管展开时间的主要因素［J］.中国空间科学技术，1996，16（1）：20－25.

［2］王成轩，毕训银，苏成，等.冲击对双节套筒式延伸喷管展开特性的影响［J］.中国空间科学技术，1996，16（6）：8－11.

［3］尤军峰，校金友，张铎，等.固体火箭发动机延伸喷管展开动力学分析［J］.推进技术，2008，29（1）：37－42.

［4］Li Jun，Xing Jun－wen，TanWen－jie，et al.ADAMS practical case tutorial［M］.Beijing：Beijing Institute of Technology，Publisher，2002.

［5］Li Zeng－gang.ADAMS elementary explanation in detail and practical case［M］.Beijing：National Defense Industry Publisher，2006.