高次驻波谐振定量检测弹性板厚度的方法
王禹然,张 辉,张淑仪
(南京大学 声学研究所 近代声学实验室,南京 210093)
提出一种基于高次驻波谐振的测量方法,研究弹性板厚度对具有最大有效机电耦合系数的谐振模式频率偏移的影响,并定量检测弹性板厚度的变化。此方法可以对金属、非金属和复合材料等进行无损检测,且设备简单、易于操作。
首先介绍高次驻波谐振的理论;其次对具有最大有效机电耦合系数的模式进行分析,给出该模式数的修正公式;最后建立该模式谐振频率偏移与检测弹性板厚度之间的关系。以ZnO 为压电片,针对不同声阻抗的弹性板厚度变化进行数值计算与研究。
1 高次驻波谐振理论
将厚度膨胀振动的压电片置于被检测弹性板之上,如果两者之间耦合紧密,则构成高次驻波谐振结构,如图1所示。其中压电片和其上下表面的两个电极构成的换能器在弹性板中激发厚度膨胀振动声波,当激发的声波半波长的整数倍与弹性板厚度相等时,将在弹性板中形成驻波谐振。一般情况下,弹性板的厚度较压电片厚很多,所以声波能量主要集中于板中。这样,检测系统的谐振特性将受到弹性板材料、表面状况和厚度等的影响。

图1 片状换能器测弹性板厚度变化的系统
上述高次驻波谐振结构可以利用Mason等效电路理论[1]进行分析。此检测系统的压电换能器输入阻抗Zin表示为[2]:
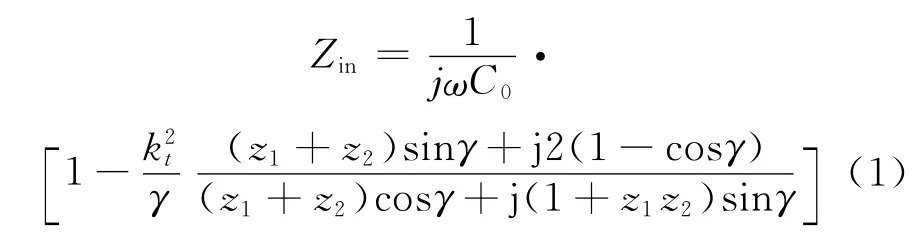
根据式(1),针对厚度为0.05mm 的PZT 压电片和厚度为2.4mm 的不锈钢弹性板,计算其输入电阻抗曲线,如图2 所示。可以看出,随着频率增加,激发出许多高次谐振模式。每一个谐振模式包括并联谐振频率fp和串联谐振频率fs。为简化分析,引入并联谐振频率间隔Δfp作为分析参量,具体定义为:
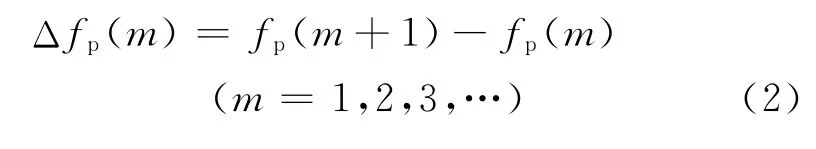

图2 输入电阻抗曲线
式中fp(m+1)和fp(m)分别是高次驻波谐振系统在第m+1和第m阶模式的并联谐振频率。
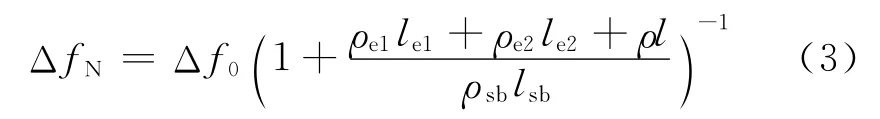
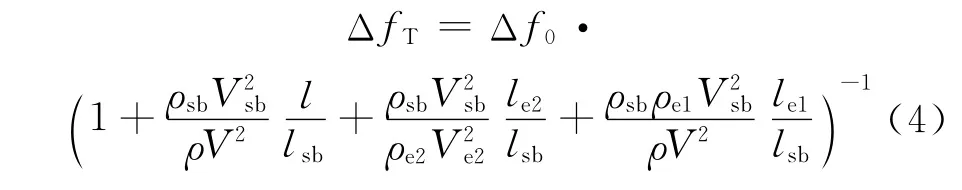
式中ΔfN指并联谐振频率间隔分布中的第一个稳态区域中间模式(mN)所对应的并联谐振频率间隔,γ≈π;ΔfT指并联谐振频率间隔分布中的第一个瞬态区域中间的模式(mT)所对应的并联谐振频率间隔,γ≈0.5π;而Δf0=Vsb/2lsb,指弹性板厚度膨胀振动时的并联谐振频率间隔。
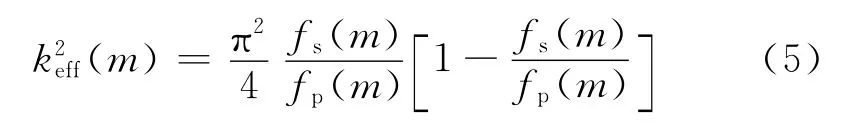
以下电极的二分之一处为分界线,将高次驻波谐振系统分为两层,引入上下两层的半波长谐振频率比例因子R。当R足够大时,稳态区域和瞬态区域中间的模式可近似表示为:mN=round(R),mT=round[(R-1)/2],其中R为[2]:
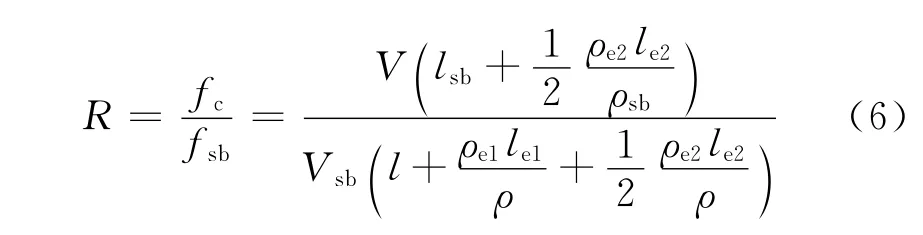
实际测量中,为避免压电片激发带宽的影响,通常采用压电片基模谐振频率附近区域的驻波谐振模式。在文献[4]的研究中,已经指出最大有效机电耦合系数对应的高次驻波谐振模式在第一稳态和瞬态区域附近,且在测量中该模式具有较大的阻抗幅值,因此该模式最适宜用以研究弹性板厚度的变化。
2 弹性板声阻抗对(max)对应谐振模式的影响
最大有效机电耦合系数所对应的谐振模式具有较高的阻抗幅值,且容易激发而获得较高的检测灵敏度,所以利用其作为检测模式[5]。Wang[6]等人分析了具有最大有效机电耦合系数的谐振模式,重点研究其模式数的变化规律。
如果根据弹性板和压电片声阻抗比zb=(ρsbVsb)/(ρV)来确定对应模式的次数,可有以下三种情形:①zb≫1,为硬基片条件落在瞬态区域中间,即mT附近,对应频率约为f=V/4l。②zb≪1,为软基片条件落在稳态区域中间,即mN附近,对应频率约为f=V/2l。③zb在1 附 近 时(max)对应的模式数则落在mT和mN的之间。所以,只有“很硬”或“很软”的压电片和弹性板组合对应的模式次数可以用mT或mN近似表示外,其它情形下,将难以估算对应的模式次数。
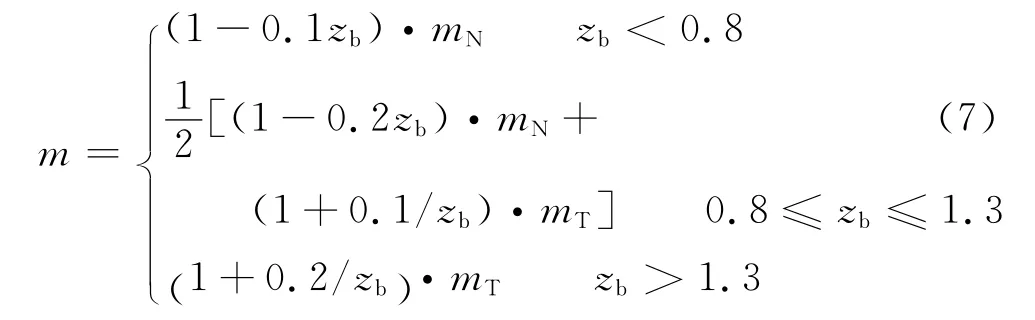
利用式(7),针对压电片材料为ZnO 和PZT 的片状换能器在不同声阻抗的弹性板上的情形进行数值计算。计算中片状换能器厚度取1 mm,上下电极厚度取为1μm 的Al电极,弹性板厚度的选取满足R≈50,相关材料的参数如表1 所示,其中PZT材料的制备方法为sol-gel[6]。相关计算结果如图3,图中圆圈点表示Wang等人推荐的估算方法得到的对应的模式次数,而方块点表示采用修正公式(7)得到的对应的模式次数。根据计算结果可知,加入zb参量后的修正公式估算得到的模式次数,更接近或等于大量数值计算得到的(max)对应的模式次数。修正前后的估算公式所得到的模式次数与k2eff(max)对应的模式次数的相对误差如表2所示。可以看到修正后的相对误差明显小于修正前的相对误差,这说明修正公式是有效的。
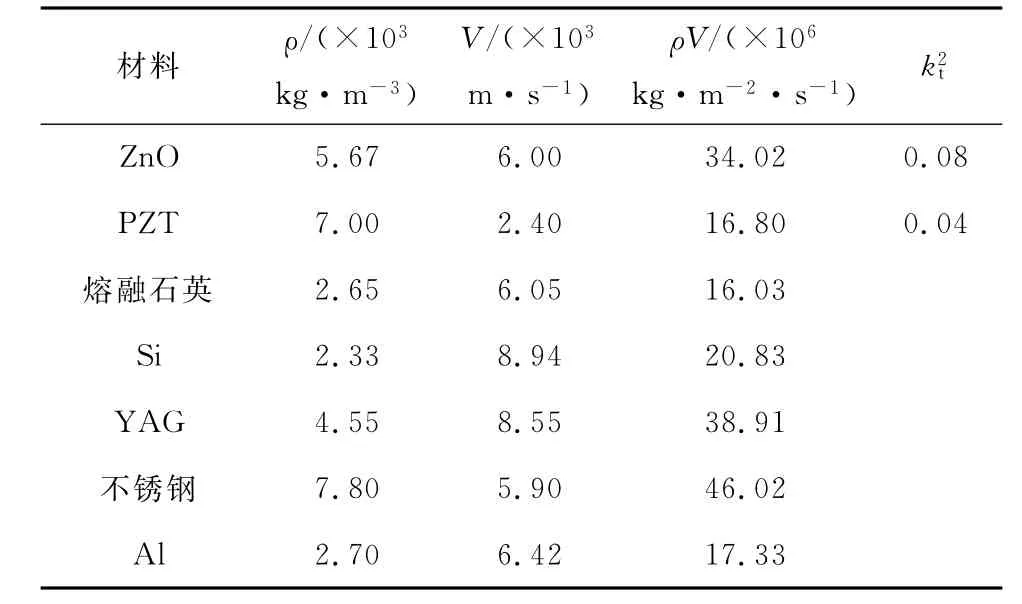
表1 压电片、弹性板和电极的材料参数
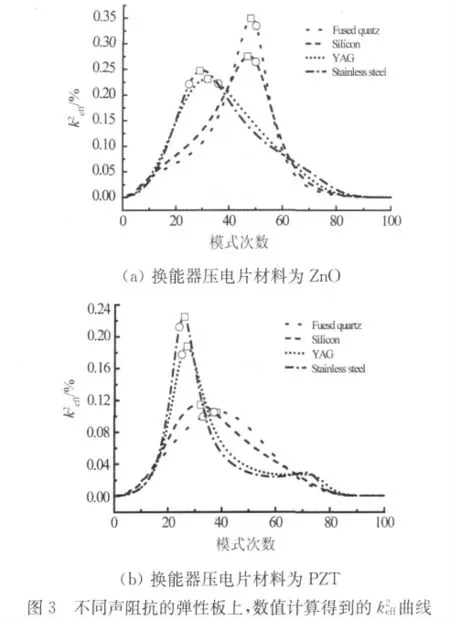

表2 修正前后的估算得到的模式次数与k2eff(max)对应的模式次数的相对误差
3 弹性板厚度变化与(max)对应谐振模式Δfp 间的关系
由于弹性板厚度的变化会导致并联谐振频率发生偏移,通过建立它们之间的解析关系可以定量表征弹性板的厚度变化。根据并联谐振频率间隔分布理论,在稳态区域,已知[2]:

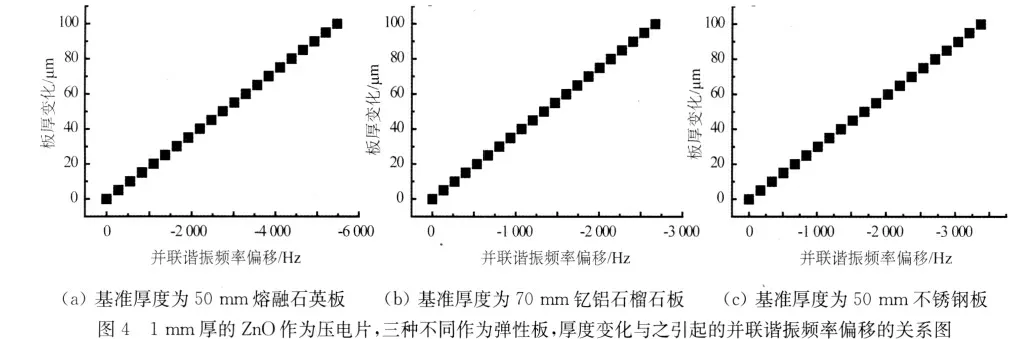
在片状换能器中,若电极的厚度相对压电片而言很薄,则忽略电极的影响。在模式数尚未发生跳变的情况下,推导弹性板厚度变化Δl时,并联谐振频率的偏移为:
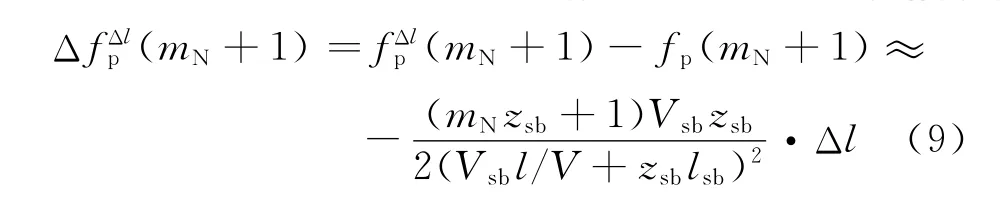
类似的,在瞬态区域,已知[2]:
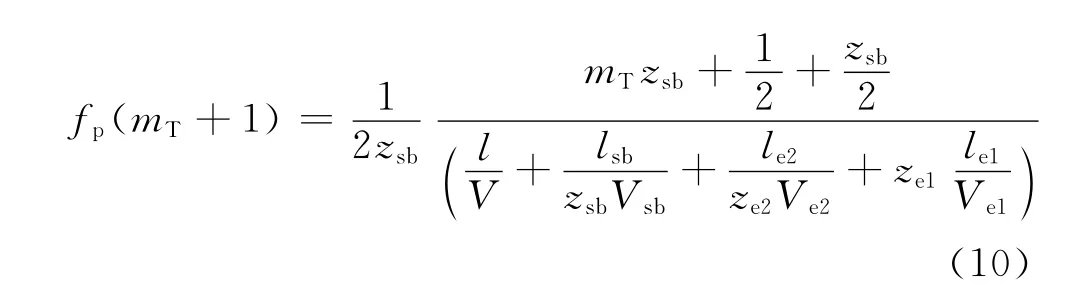
忽略电极的影响,并联谐振频率的偏移为:
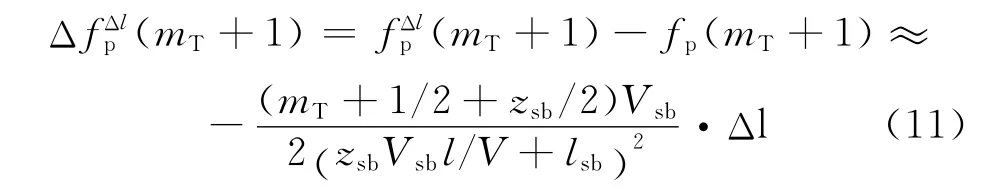
式(9)和(11)说明,弹性板厚度变化Δl所引起的并联谐振频率偏移Δfp与Δl成线性关系。因此,若选择待测弹性板作为基片层,选定已知厚度的弹性板作为参照基准,测量待测弹性板与基准弹性板在对应频率的差值,就可以间接得到待测板与基准板的相对厚度变化。
针对具有最大有效机电耦合系数的谐振模式,采用1mm 厚ZnO 作为压电片,熔融石英、钇铝石榴石、不锈钢作为弹性板,研究弹性板厚度增加时厚度变化与之引起的并联谐振频率偏移的关系,相关计算结果如图4所示。数值计算表明,基准弹性板厚度满足R≈50时对应的并联谐振频率fp每偏移数十赫兹可定量检测出1μm 厚的弹性板厚度变化。
4 结论
[1] Lakin K M,Kline G R,McCarron K T.High-Q microwave acoustic resonators and filters[J].Microwave Theory and Techniques,IEEE Transactions,1993,41(12):2139-2146.
[2] Zhang Y X,Wang Z Q,Cheeke J D N.Resonant spectrum method to characterize piezoelectric films in composite resonators[J].Ultrasonics,Ferroelectrics and Frequency Control,IEEE Transactions,2003,50(3):321-333.
[3] IEEE Standard on Piezoelectricity ANSI/IEEE Std 176-1987,1988[S].
[4] Zhang H,Zhang S Y,Zheng K.Electrode effects on general modes in high-overtone bulk acoustic resonators[J].Ultrasonics,2006,44(S1):e737-e740.
[5] Zhang H,Zhang S Y,Fan L.Effects of thickness deviation of elastic plates in multi-layered resonance systems on frequency spectra[J].Chinese Physics Letters,2009,26(8):4301
[6] Pao Shih-Yung,Chao Min-Chiang,Wang Zuoqing,et al.Analysis and experiment of HBAR frequency spectra and applications to characterize the piezoelectric thin film and to HBAR design[C].Frequency Control Symposium and PDA Exhibition,2002.IEEE International:2002:27-35.

