长方形构件的拟合研究

沈丹华 蔡荣华 林志宏 戴明如

(1.浙江省测绘大队,浙江杭州 310030;2.浙江省温岭市国土局,浙江温岭 317500;3.浙江省温岭市测绘队,浙江温岭 317500)

要检测某长方形构件,需要检测其表面是否平整,尺寸是否符合设计要求。在其表面适当位置粘贴标志,在附近安置全站仪,观测这些标志的空间坐标,计算其平整度和长方形的尺寸。具体步骤如图1。

图1 拟合空间长方形流程

1 拟合平面求平整度

图2表示长方形在空间的位置。它与测量坐标系(o-xyh)的关系是任意的。o-h方向为垂线方向。o-xy面为水准面的切面,全站仪安置在空间长方形的旁边,采用自由设站直接测定目标的三维坐标。

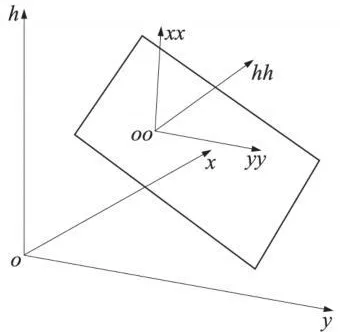
图2 空间长方形与测量坐标系关系

由于施工误差或观测误差,这些标志并不完全在同一平面内,设要拟合的平面方程为

式中(a b c)T为平面的法线方向单位矢量,a＞0,若a=0 则b＞0,若a=0 且b=0则 c＞0,a、b、c不可能同时为0。

以(xiyihi)T(i=1,2,…,n)表示观测点坐标。

为了避免由于直线平行于某坐标轴而出现数值问题,求出测(xiyihi)T(i=1,2,…,n)中的3个坐标分量的最大值和最小值之差 Δx、Δy、Δh。

在 Δx、Δy、Δh 中,若 Δx 最小 ,则按 x=ay+bh+c拟合,若 Δy最小,则按 y=ah+bx+c拟合,若 Δh最小,则按h=ax+by+c拟合。

另外,也可以先将坐标分量变换至[-1 1]区间,拟合后再回代。

求得平面方程(1)后,i点至平面的距离就是误差方程残差

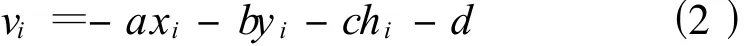
上式中的残差通常用于表示测得平面的平整度。i点在平面上的投影点坐标(xpiypihpi)T为

投影点坐标一定满足平面方程。

2 坐标转换求各个点平面坐标

在求得所有测定点在平面上的投影点坐标(xpiypihpi)T(i=1,2,…,n)后,建立平面坐标系oo-xxyyhh,如图2,此坐标系的两个轴xx、yy处在平面内,hh轴与平面的法线方向一致,各投影点在平面坐标系中的高程hh=0。

oo点在测量坐标系o-xyh中的坐标定义为

xx轴在测量坐标系o-xyh中的方向定义为oo点至面内某点(不能是oo点)的方向,不妨设为oo点至

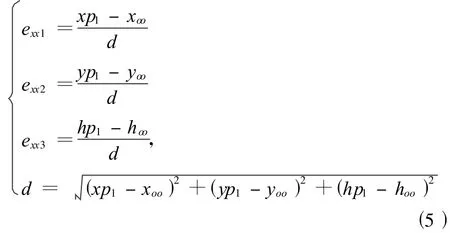
借鉴Luna24探测器和地面油田钻井工程中稳定器设计相关经验，根据钻取采样设备外部支撑装置的设计需求，本文设计了一种锁合随动式限幅机构。该机构位于钻杆的中部，在飞行工作阶段主要起到钻具的限幅作用；当钻具钻进到位之后，该机构可以实现解锁，并随钻具同步向下进尺。同时，本文基于有限元分析和地面系统级验证试验，对该限幅机构的性能进行验证。

yy轴在测量坐标系o-xyh中的方向是xx与hh的叉乘方向

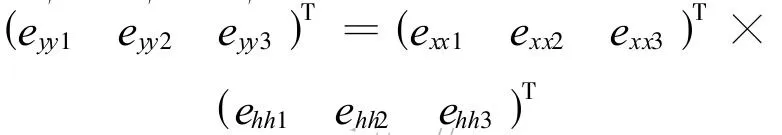
式中

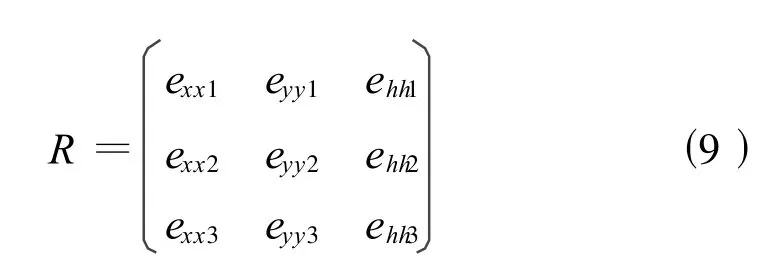
由平面坐标系中坐标求测量坐标系中坐标的转换关系为

3 拟合四条边求直角点坐标

若在长方形的四条边上分别测定了一些点,先拟合一个平面,求出投影点坐标,将所有投影点换算至平面坐标系(如图3所示)。)表示边j上测定点在平面坐标系中xy平面内的坐标。

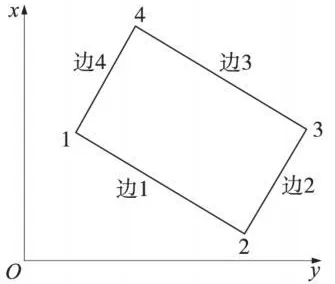
图3 拟合长方形及其需观测点

考察边1上点坐标分量的范围 Δx、Δy,若 Δx＞Δy,则边1的方程为y=ax+b1,否则方程为x=ay+b1。

对每条边上的点列出误差方程,如对边2上的点

由所有点的误差方程组成法方程求解,迭代至收敛,得到四条边的方程(若拟合前坐标变至[-1 1]区间,则应回代)。

4 由直角点坐标求边长

求得4个角点在平面坐标系中的坐标后,可求出长方形的边长,按式(10)转回测量坐标系,便可得到4个角点在测量坐标系中的坐标。

5 算例

该算例采用实测数据,其中长方形的长为1 m,宽为0.667 m。实测点坐标如表1所示。

表1 各边上实测测点坐标 m

由第2部分,式(2)拟合得平面方程的参数为

由平面实测点坐标和方程,求得各点至平面的距离Vi和投影点坐标,如表2所示。

表2 各点在平面上的投影点坐标和至平面的距离,各投影点平面坐标,观测点至拟合直线距离 m

由表2可知,各点至平面的距离反映长方形表面的平整度,显然只要在表面上增加观测点的个数,即可增加观测的客观性。由各个点的平面坐标在平面内分别拟合直线,直线相交,求得交点的平面坐标。如表3所示。

表3 4个顶点在平面坐标系中坐标 m

拟合得四条直线方程分别为

由4个点的平面坐标分别求得边长为:上边0.998 293 242 594 40 m,下边0.998 293 242 59440 m,左边0.661 459 043 585 17 m,右边0.661 459 043 585 17 m。将4个顶点在平面坐标系中坐标转换回测量坐标系中,得到4个顶点在测量坐标系中坐标,如表4所示。

表4 4个顶点投影点在测量坐标系中坐标 m

直角点的坐标旋转回测量坐标系,可比较直角点设计坐标与测的坐标的差别。

6 结束语

对于空间任意放置的长方形设备,利用全站仪采集了表面适当点的坐标后,可以由本文的模型算出长方形设备的各个参数及其形变量。该长方形设备检测的方法比较全面实用,拟合过程不会损失精度。通过实例计算说明该方法可行实用,可以准确检查工业构件的尺寸并给出精确修改值。

[1]王解先,季凯敏.工业测量拟合[M].北京:测绘出版社,2008

[2]王解先,许 琛,陆彩萍.沉管沉放的实时监测[J].测绘学报,2002,31:70-72

[3]陈基伟.工业测量数据拟合研究[D].上海:同济大学土木工程学院,2005

[4]陈俊平,王解先.工业测量中的曲线拟合[J].工程勘察,2003(5):59-61