基于地下深部工程岩体特性的RMR系统修正

刘业科，曹平，衣永亮，张向阳，陈锐

(中南大学 资源与安全工程学院，湖南 长沙，410083)

随着地下空间开发不断向深部发展，深部岩体工程具有典型的高应力、高渗透压和高温特性[1]，导致深部岩体工程的压力加剧，围岩变形加大且具有明显的流变现象，岩石强度随着时间延长而逐渐降低，岩石破坏由脆性破坏向延性破坏转变，岩爆现象显现，对深部工程的安全高效运转造成了巨大威胁。因此，对深部工程围岩质量和稳定性进行合理评价不但非常必要，而且是制定相应的支护控制措施的前提条件之一。岩体工程质量评价是对影响岩体工程设计、施工和维护的各种因素建立一些评价指标，对工程辖区岩体进行评价，划分出不同的级别或类别[2]。在众多岩体工程质量评价方法中，Bieniawski[3]提出的RMR系统，综合考虑了岩石强度、岩芯质量、节理间距、节理条件及地下水影响等方面的因素，是一种比较完善、应用广泛的工程岩体分类方法。RMR 系统是Bieniawski基于土木工程提出的，为了使这个分类系统适用于采矿工程，Bieniawski先后4次对原RMR 法进行修正，现在一般都以其1989年版本[3]为标准，见表1和表2。此外，Laubscher[4−5]提出的改进的岩体等级系统(MRMR)和 Cummings等[6]提出的MBR(Modified basic RMR)system在Bieniawski的RMR系统的基础上加入了爆破损伤、应力改变、地应力、岩体结构效应和天气等因素的影响。谢本贤等[7−8]考虑地下水、地温对岩体力学性质的影响，结合连续性细化方法对传统的RMR系统中前3个评价指标的评分标准进行了修正，根据岩体中地应力及岩石强度特征定义了岩体损伤破坏危险度系数。目前，RMR系统不断得到完善，工程适用范围不断扩大。

1 RMR法简介

RMR系统是Bieniawski于1973年提出的一种确定岩体质量等级的方法[9]。它将岩块的单轴抗压强度(P1)、岩石质量指标(P2)、节理间距(P3)、节理状况(P4)、地下水状况(P5) 及根据节理面的方位与基础、边坡、洞室方向关系确定的修正系数(P6)共 6个指标作为基本参数，根据岩体状况逐一评分、相加，则可得到岩体质量的RMR总评分PRMR：

这6个基本指标及其评分标准如表1 所示。由表1 和式(1) 得到岩体的PRMR后，可据表2对岩体质量进行等级划分。

表1 RMR系统分类指标及评分Table 1 Classification indexes and their ratings of RMR system

表2 RMR 系统岩体质量分类Table 2 Rock mass classes determined from total ratings of rock mass rating system

2 RMR系统的修正

随着RMR系统的不断修正和完善，其在浅部岩体工程中适用性越来越好。但从深部岩体的特点出发考虑 RMR系统时，该方法在高地应力、岩石变形的时间效应(流变)、高地温和岩石含水性影响等因素考虑不够，加上分类中的权值离散，造成适应性较差。为此，需要通过深入分析深部工程中的不良地质因素对岩体质量的影响，对传统的 RMR系统进行合理修正，使其更加符合深部岩体工程实际，从而更好地为深部工程围岩质量评价服务。

2.1 RMR系统的单轴抗压强度(σc)修正

传统的RMR系统中P1项为完整岩石强度，分为现场进行的点荷载强度(σIs)和室内进行的抗压强度(σc)2类。其中：点荷载强度是在现场实测，与工程实际更接近，但是需要将仪器带到现场，且受到很多现场环境限制。而室内进行的抗压强度实验，操作方便，费用低，便于观测，但由于室内实验环境与现场实际环境存在很大差异，因此，直接使用室内的抗压强度作为P1的评分参数是不合适 的。为了解决这些问题，本文作者从深部岩体的地下水、温度和岩石流变3个方面对单轴抗压强度(σc)进行修正。

地下水对岩体的作用主要表现为对岩体结构面和结构体力学性质的弱化作用。深部岩体工程大多处于原地下水潜水面以下，在高地应力的影响下，地下水压往往很大，高地下水压增强了地下水对岩块的软化作用，使岩石的吸水性增大，离子交换和水解速度加快，孔隙动、静水压增大，从而加深了水对岩石的弱化作用。传统的 RMR系统考虑了地下水对岩体结构面的影响，但未考虑地下水对完整岩块力学性质的弱化影响，故在实际工程中的岩块强度往往低于常规室内试验所确定的岩块强度。因此，有必要对 RMR系统中完整岩石强度指标进行地下水对岩体强度的弱化系数修正。考虑地下水对岩体强度弱化作用常用的公式为：

式中：σcb为饱和岩石单轴抗压强度；cσ为干燥状态下岩石的单轴抗压强度；cη为岩石的软化系数。

由式(2)得到的岩石软化系数为常数，而自然界中的工程岩体并不是所有的都处于干燥或者饱和2种绝对状态，不同区域的岩石含水率不同。试验表明[10−11]：随着岩石含水率的变化，岩石强度是不断变化的，因此，岩石的强度是与含水率w(质量分数)相关的函数。通过对文献[10−11]中的数据进行分析发现：含水率增长与岩石强度下降并非简单的线性关系，含水率的增长速度与岩石强度的下降速度的比值先逐渐增大再逐渐下降。对其进行拟合发现：非线性Boltzmann函数曲线拟合比线性拟合相关系数更高，即

式中：σw为地下水弱化后的岩石单轴抗压强度；w0为特定含水率，当w = w0时，σw=(σc−σcb)/2；d为含水率变化幅度，σw在(w0−d，w0+d)范围内变化。当采用点载荷强度时，其定义类似。

本文定义完整岩石强度指标σc的水弱化修正系数Rw为：

将式(2)和(4)代入式(3)，得 Rw与含水率 w 的Boltzmann函数非线性关系，即：

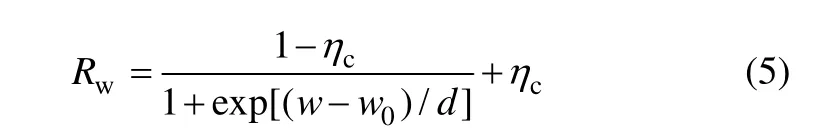
深部岩体工程的一个显著特征就是地温偏高。据文献[12]报道：越往地下深处，地温越高。地温梯度一般为 30～50 ℃/km，深部岩体内的温度常为 40～50 ℃。温度对岩体的弱化作用由热物理力学作用和热化学作用2个因素造成。其中：以热物理力学作用为主，岩石中的各种矿物颗粒在高温条件下的热膨胀系数各不相同，受热后的变形也不同，但岩石为了保持其变形的连续性，不允许内部的各矿物颗粒按各自固有的热膨胀系数自由变形，于是，颗粒之间就产生了约束，造成受压、受拉，从而在岩石中产生了结构热应力。温度升高，岩体在结构热应力的作用下结构发生改变，产生微裂隙，变成碎裂结构，强度下降。而岩石的热化学作用局限于高温条件下岩石中的矿物颗粒发生脱水、晶型转变和晶体析出等。对 RMR系统的σc进行热弱化修正时，本文定义了一个岩石热弱化修正系数Rθ，表达式为：

式中：σθ为热弱化后的岩石单轴抗压强度。当采用点载荷强度时，其定义类似。且岩石热弱化系数Rθ与温度变化相关，通过拟合发现，两者关系近似为线性关系，表达式为：

式中：A和B为实验数据拟合确定的常数；θ为岩石温度，℃。

由于岩体属非均质、不连续、各向异性的流变介质，流变特性是其重要的力学特征之一。岩体在长期荷载的作用下，抵抗破坏的能力被削弱，应力应变状态和变形破坏特征均随时间而不断变化，具有显著的时间效应。而深部岩体受到环境中存在的高地应力影响，其力学性质发生了重要变化，表现为岩石的破坏由脆性破坏向延性破坏或延性流变转变，岩石的流变效应明显增强[13]。一般的大型岩土工程，其服务年限为几年到几十年，甚至为永久工程，因此，不仅要考虑施工期间的安全，而且要确保在其服务年限内整个系统的安全。但是，传统的RMR系统中的σc为瞬时单轴抗压强度，没有考虑其受岩石流变强度下降的影响，需要对σc进行岩石流变的弱化修正，使其能反映不同时间的岩石强度。在对RMR系统的σc进行岩石流变弱化修正时，本文定义了一个岩石流变弱化修正系数Rr，表达式为：

式中：tσ为经岩石流变弱化后任一时间t时岩石的单轴抗压长期强度。由于岩石在长期载荷作用下，岩石的强度随着时间的推移而降低，是时间的函数σ(t)，在标准加载速率下测得的强度cσ可以近似看成是岩石的瞬时强度，而 t→∞时的强度称为岩石长期强度极限σ∞；当给岩石施加的应力水平为cσ～σ∞时，岩石发生非衰减蠕变，应力越小，岩石发生破坏需要的时间越长；当应力水平低于σ∞时，岩石只发生衰减蠕变，永远不会发生破坏[14]，如图1和图2所示。

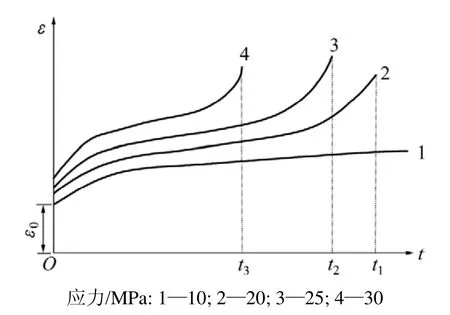
图1 不同应力下岩石蠕变曲线示意图Fig.1 Creep curve of rocks under different stress level

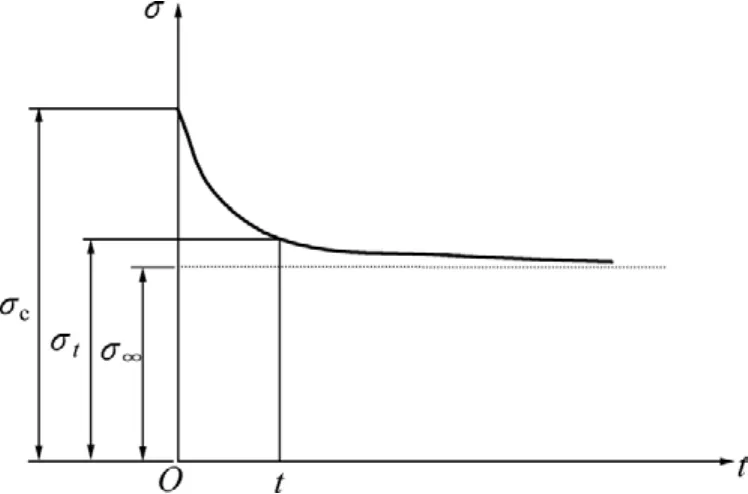
图2 岩石蠕变长期强度曲线示意图Fig.2 Creep long-term strength curve of rocks

由图1可知：取各次非衰减蠕变达到破坏时的应力tσ和荷载经历时间t得到的岩石长期强度曲线是指数衰减函数曲线，本文用指数型方程表征经岩石流变弱化后的岩石单轴抗压长期强度方程，表达式为：

把t=0，tσ=cσ和t→∞，tσ=σ∞代入式(9)，解得C=σ∞，D=cσ−σ∞，故式(9)可写成：

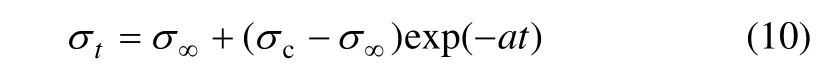
将式(8)代入式(10)消去tσ，可得Rr的表达式为：

式中：a为试验确定的常数；σ∞为t→∞时的岩石长期强度极限。

综合式(4)，(6)和(8)，可以得到同时考虑深部岩体的地下水、温度和岩石流变3个方面的特性对单轴抗压强度cσ进行修正后的单轴抗压强度σcm为：

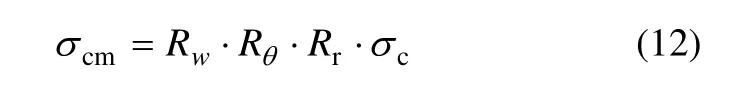
将式(5)，(7)和(11)代入式(12)得：

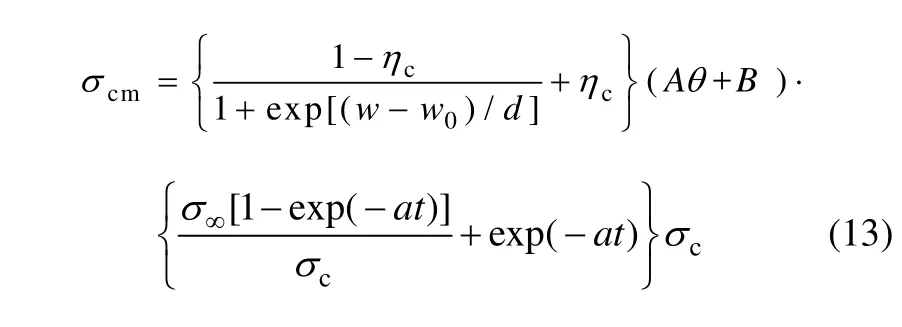
2.2 RMR系统的地应力修正

深部岩体的另一个显著特征就是存在高地应力，这是深部岩体工程围岩产生破坏失稳的主要原因之一。实测结果表明[15−16]：深部工程中原岩压力明显增大，在1.6 km 深度处压力可达40 MPa 以上。地应力中构造应力的作用显著增强，两水平地应力普遍大于垂直地应力。高地应力的存在使深部岩体的力学性质发生了重要变化，岩石由脆性破坏向延性破坏转变，岩石的强度也在微破裂效应和应力腐蚀的双重不利因素影响下进一步降低。而传统的RMR系统指标中没有考虑地应力的影响，这在浅部岩体地应力不大的地区是可行的，但在深部岩体高地应力区域，必须考虑地应力的影响，因此，本文提出一个地应力修正指标P7，具体评分见表3。

表3 RMR系统地应力修正Table 3 Revision of rock mass rating system considering in situ stress

2.3 RMR系统分类指标连续性修正

对传统RMR系统的单轴抗压强度cσ进行修正并加入地应力修正指标P7后，已改进的新RMR系统的7个评价指标能较好地描述影响岩体性质的主要因素，但其P1，P2，P3和 P7这 4个指标的评分权值是模糊离散的。如：按照表1的标准，当室内岩石单轴抗压强度cσ为249 MPa和101 MPa 时，都有评分权值P1=12；而实质上2种岩石的抗压强度相差很大，这显然是不合理的。又如：当室内岩石单轴抗压强度cσ为101 MPa和99 MPa的岩石，按表1 的标准，其权值分别为P1=12和P1=7，而实际上这2种岩石的抗压强度相差很小。其他3个因素即岩体质量、结构面间距和地应力的确定也存在类似的问题。因此，很有必要对P1，P2，P3和 P7这 4个指标的评分权值连续化修正，其结果见表4。根据表4中的结果，采用非线性回归方法，得到4个分类指标与分类参数评分值之间的连续性方程(14)～(17)：

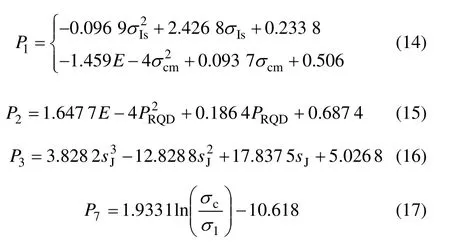
图3～7所示为由式(14)～(17)得到的非线性回归修正曲线，曲线拟合相关系数分别为0.995，0.999，1.000和 0.992。由图3～7可见：通过非线性回归获得的连续性修正方程能较好地反映分类指标与分类参数评分值之间的对应变化关系，与Bieniawski等[3]研究的线性拟合结果精度更高。进行连续化修正后，P1，P2，P3和P7这4个指标的评价边界值由一范围值转变成1个点值，消除了传统RMR系统评价标准的模糊离散性。

2.4 新修正后的RMR系统特点

新修正后的 RMR系统综合考虑了地下深部工程岩体高应力、高渗透压和高温特性和流变性的影响，通过定义岩体的水弱化修正系数Rw、温度弱化修正系数Rθ和岩石流变弱化修正系数Rt对岩石的单轴抗压强度σc进行修正，增加地应力修正项P7，并对分类指标P1，P2，P3和P7进行连续性修正，消除了传统RMR系统评价标准的模糊离散性。与谢本贤等[7−8]建立的RMR系统相比，本文建立的新RMR修正系统在考虑地下水影响时采用非线性Boltzmann函数曲线拟合，比线性拟合相关系数更高；考虑深部岩体流变特性对岩体质量的影响；提出的地应力修正指标P7考虑了地应力中的最大主应力σ1与室温下干燥岩石单轴抗压强度σc之比对岩体质量的影响；在进行RMR系统分类指标连续性修正中，分别对 P1，P2，P3和 P7进行了非线性2次、2次、3次和对数连续性修正。

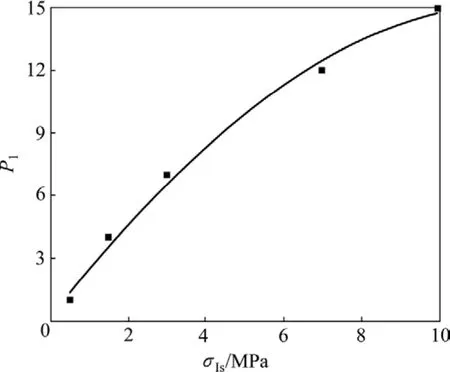
图3 点载荷指标的P1非线性回归曲线Fig.3 Nonlinear fitting curve of P1 and point-load strength index

图4 单轴抗压强度指标的P1非线性回归曲线Fig.4 Nonlinear fitting curve of P1 and uniaxial compressive strength

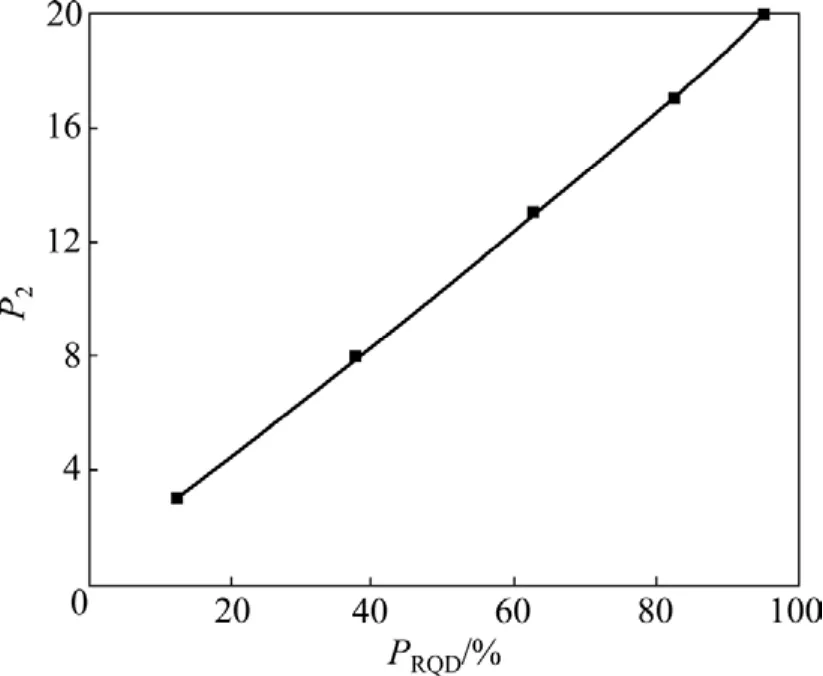
图5 RQD指标的P2非线性回归曲线Fig.5 Nonlinear fitting curve of P2 and drill core quality RQD

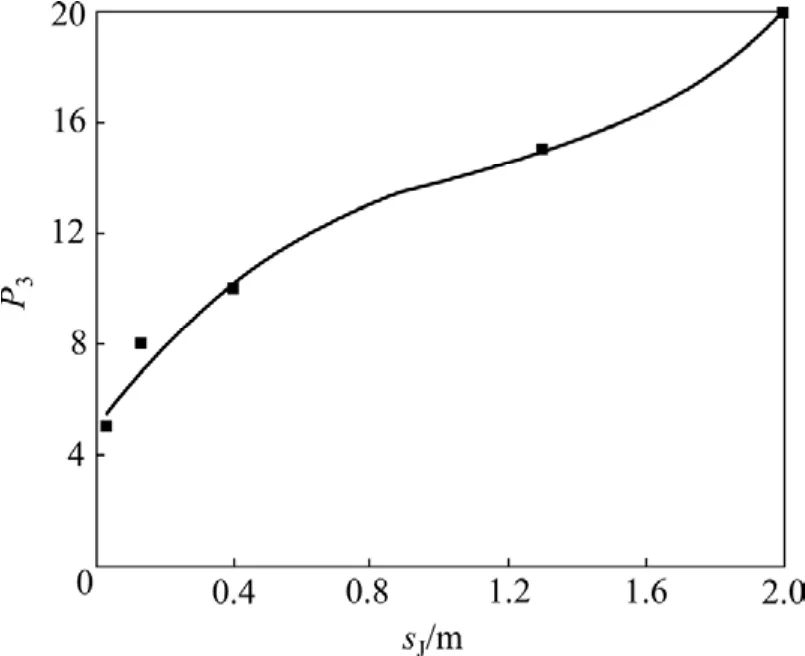
图6 节理间距sJ的P3非线性回归曲线Fig.6 Nonlinear fitting curve of P3 and spacing of discontinuities

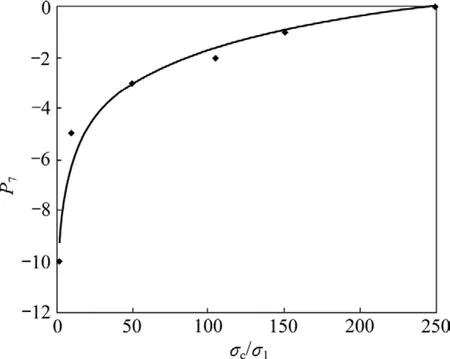
图7 地应力指标的P7非线性回归曲线Fig.7 Nonlinear fitting curve of P7 and in situ stress

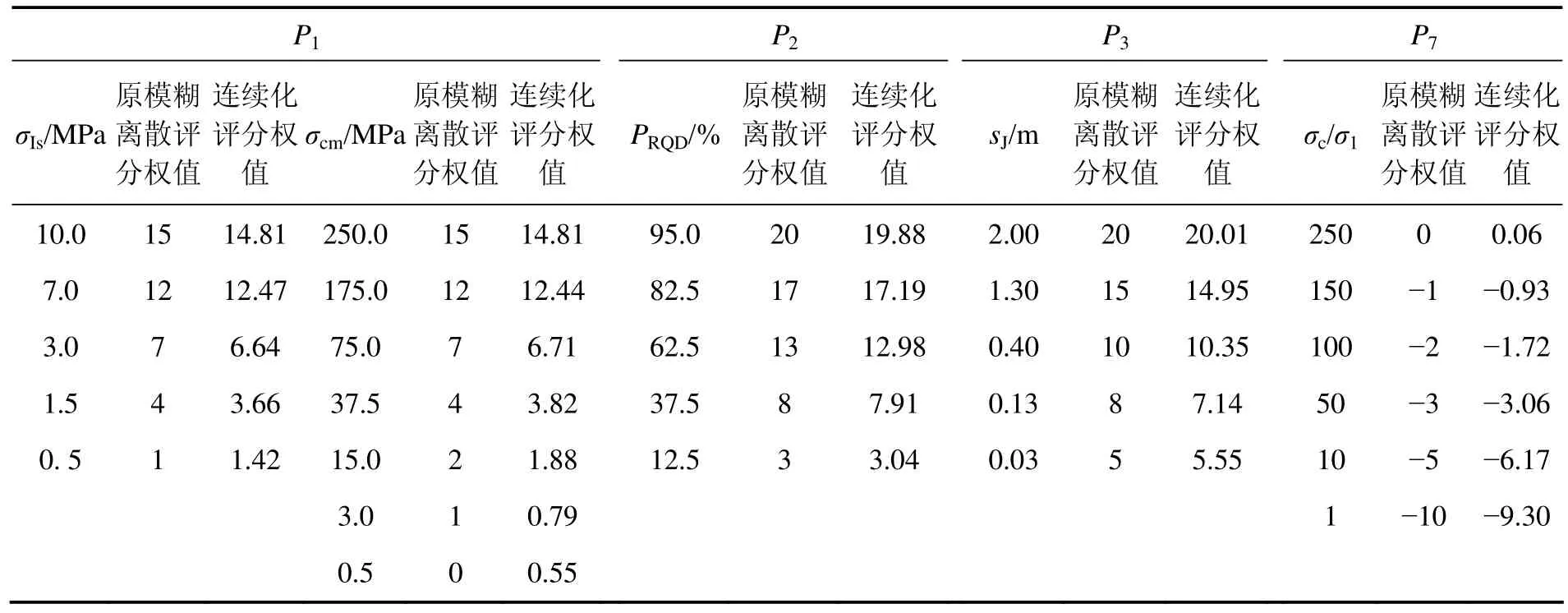
表4 RMR系统分类指标P1，P2，P3和P7连续性修正Table 4 Continuity revision of P1, P2, P3 and P7 of rock mass rating system

3 修正后的RMR系统工程应用实例

本试验的二辉橄榄岩采自某镍矿地下 800 m水平，该处地应力中最大主应力σ1为37.26 MPa[17]，室温下干燥岩石单轴抗压强度 σc为 59.423 MPa，P7=σc/σ1=1.595，根据表3可知：该地区属于高地应力区。岩石的水弱化修正系数Rw与含水率w采用Boltzmann函数非线性拟合，岩石的温度弱化系数Rθ与温度θ采用线性拟合，流变弱化修正系数Rt与荷载经历时间t采用指数衰减函数拟合，见图8～10和式(18)～(20)，拟合曲线的相关系数分别为0.995，0.995和0.998。该镍矿的二辉橄榄岩单轴抗压强度σc的3类弱化系数数据见表5。

由传统的RMR系统和上述修正法获得二辉橄榄岩在不同时间、不同含水率、不同温度下的岩体质量评分结果，如表6所示。由表6可见：采用修正后的RMR系统评价该镍矿的二辉橄榄岩的岩体质量时，随着岩石流变荷载经历时间、含水率、温度和地应力的增加，岩体质量评分值降低为传统的RMR系统评分值的83.6%～70.2%，岩体质量等级部分保持不变，部分从Ⅲ降到Ⅳ级，所得结果与深部地下工程岩体状况相符程度比传统的RMR系统评分的相符程度更好。

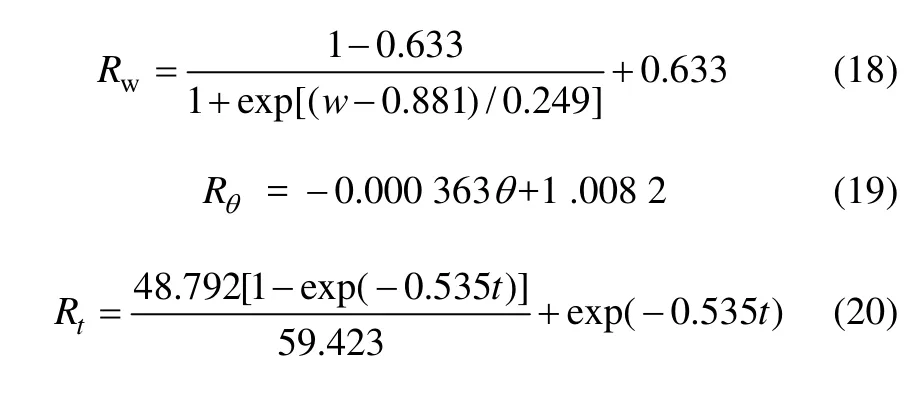
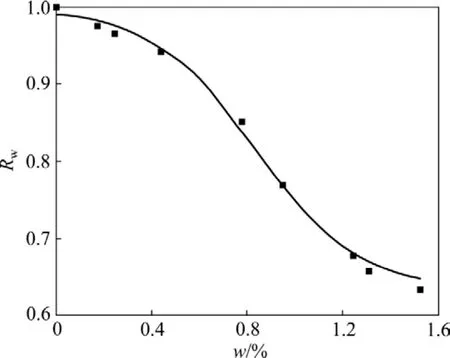
图8 地下水弱化修正系数与含水率的关系Fig.8 Relationship between groundwater weakening fitting coefficient and water content

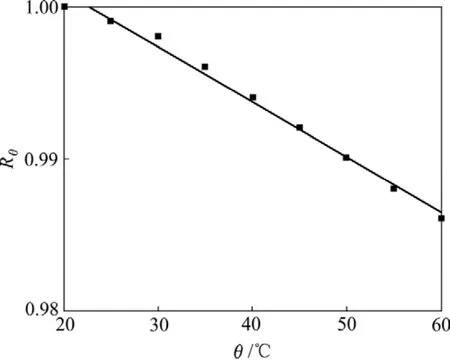
图9 温度弱化修正系数与岩石温度的关系Fig.9 Relationship between temperature weakening fitting coefficient and rock temperature

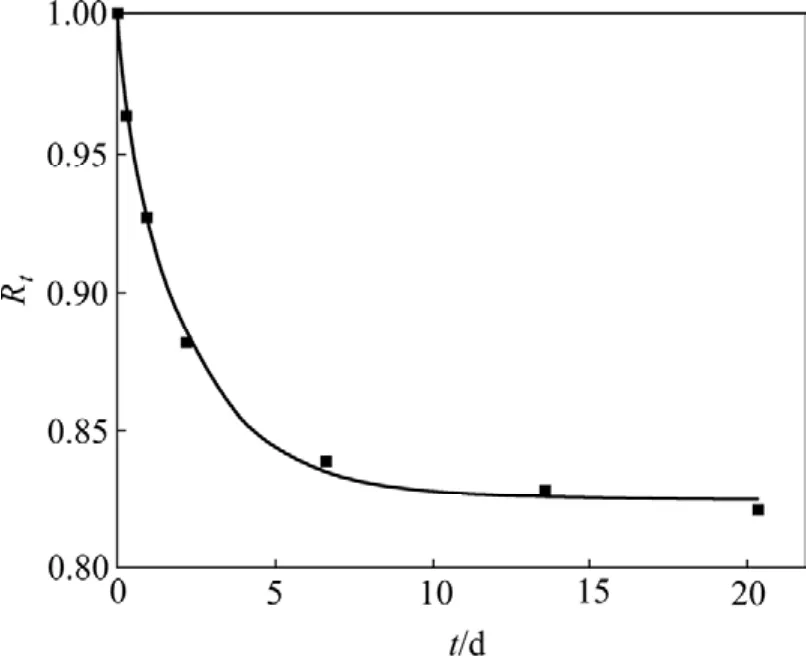
图10 流变弱化修正系数与岩石受压时间的关系Fig.10 Relationship between rheology weakening fitting coefficient and rock compressed time

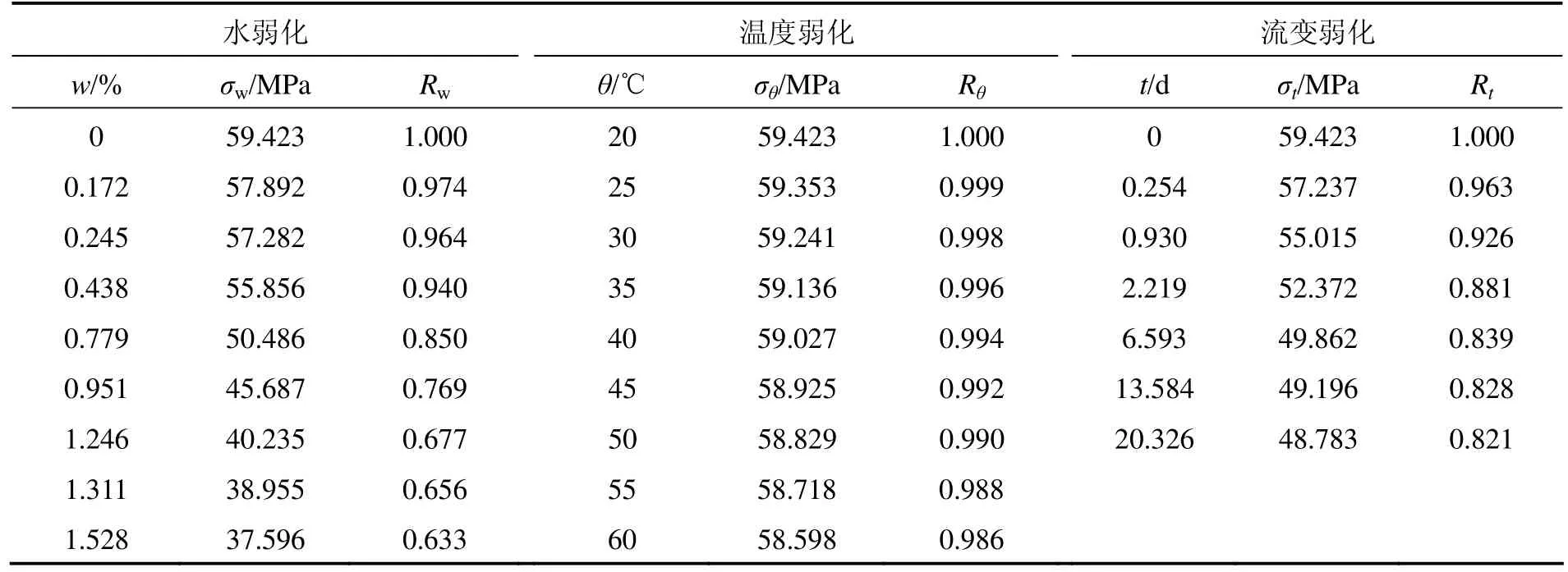
表5 某镍矿二辉橄榄岩的地下水、温度和流变弱化修正系数Table 5 Data of groundwater, temperature and rheology weak coefficients of picrite in a nickel mine

表6 某镍矿二辉橄榄岩的修正RMR系统评分Table 6 Revised RMR system evaluation of picrite in a nickel mine

4 结论

(1) 深部岩体处于典型的高地应力、高温、高地下水压场中，地下水、地温、地应力和岩石流变造成岩体质量下降，因此，采用传统的浅部岩体质量评价方法RMR系统对其围岩质量进行评价是不够合理的。

(2) 定义岩体的水弱化修正系数Rw、热弱化修正系数 Rθ和岩石流变弱化修正系数 Rt对岩石的单轴抗压强度σc进行修正，增加地应力修正项P7，对分类指标P1，P2，P3和P7进行连续性修正，消除了传统RMR系统评价标准的模糊离散性，获得了比较符合深部岩体工程围岩质量评价实际状况的修正 RMR系统。实例表明，该修正 RMR系统评价结果合理有效，可在深部工程实际中推广应用。

(3) 修正后的RMR系统中，水弱化修正系数(Rw)、热弱化修正系数(Rθ)和岩石流变弱化修正系数(Rt)分别与岩石含水率(w)、岩体温度(θ)和岩石流变荷载时间(t)满足非线性Boltzmann函数、线性函数和非线性指数衰减函数关系，曲线拟合相关系数都在0.995以上，随着含水率、温度、时间和地应力的增加，修正RMR系统的岩体质量评分值比传统的RMR系统岩体质量评分值低，等级略有下降，所得结果与深部地下工程岩体状况更吻合。

[1]何满潮, 谢和平, 彭苏萍, 等. 深部开采岩体力学研究[J]. 岩石力学与工程学报, 2005, 24(16): 2803−2813.HE Man-chao, XIE He-ping, PENG Su-ping, et al. Study on rockmechanics in deep mining engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(16): 2803−2813.

[2]王文星. 岩体力学[M]. 长沙: 中南大学出版社, 1999:117−121.WANG Wen-xing. Rock mass mechanics[M]. Changsha: Central South University Press, 1999: 117−121.

[3]Bieniawski Z T. Engineering rock mass classification[M]. New York: Science Press, 1989: 180−250.

[4]Laubscher D H. Geomechanics classification of jointed rock masses-mining application[J]. Transactions of the Institution of Metal Mines, 1977, 86: A1−A8.

[5]Laubscher D H. Design aspects and effectiveness of support systems in different mining conditions[J]. Transactions of the Institution of Metal Mines, 1984, 93: A70−A82.

[6]Cummings R A, Kendorski F S, Bieniawski Z T. Caving rock mass classification and support estimation[R]. Chicago: US Bureau of Mines, 1982.

[7]谢本贤, 陈沅江, 史秀志. 深部岩体工程围岩质量评价的IRMR法研究[J]. 中南大学学报: 自然科学版, 2007, 38(5):987−992.XIE Ben-xian, CHEN Yuan-jiang, SHI Xiu-zhi. IRMR method for evaluation of surrounding rock quality in deep rock mass engineering[J]. Journal of Central South University: Science and Technology, 2007, 38(5): 987−992.

[8]陈沅江, 吴超, 傅衣铭, 等. 基于修正 RMR法的深部岩体工程围岩质量评价研究[J]. 防灾减灾工程学报, 2007, 27(2):141−146.CHEN Yuan-jiang, WU Chao, FU Yi-ming, et al. Study on evaluation of the surrounding rock quality in deep rock mass engineering based on the revised RMR method[J]. Journal of Disaster Prevention and Mitigation Engineering, 2007, 27(2):141−146.

[9]Bieniaski Z T. Engineering classification of jointed rock masses[J]. Transaction of the South African Institution of Civil Engineering, 1973, 15(12): 335−344.

[10]康红普. 水对岩石的损伤[J]. 水文地质工程, 1994(3): 39−41.KANG Hong-pu. Rock damage from water effect[J].Hydrogeology Engineering, 1994(3): 39−41.

[11]朱珍德, 邢福东, 王思敬, 等. 地下水对泥板岩强度软化的损伤力学分析[J]. 岩石力学与工程学报, 2004, 23(S2):4739−4743.ZHU Zhen-de, XING Fu-dong, WANG Si-jing, et al. Analysis on strength softening of argilite under groundwater by damage mechanics[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(S2): 4739−4743.

[12]陈沅江, 潘长良, 曹平, 等. 一种软岩流变模型[J]. 中南工业大学学报: 自然科学版, 2003, 34(1): 16−20.CHEN Yuan-jiang, PAN Chang-liang, CAO Ping, et al. A new rheological model for soft rocks[J]. Journal of Central South University of Technology: Natural Science, 2003, 34(1): 16−20.

[13]范广勤. 岩土工程流变力学[M]. 北京: 煤炭工业出版社,1993: 2−3.FAN Guang-qin. Geotechnical engineering rheology mechanics[M]. Beijing: China Coal Industry Publishing House,1993: 2−3.

[14]CHEN Yuan-jiang, CAO Ping, PAN Chang-liang. Study on the structural effect of soft rock rheology[C]//LUO Ying-she, RAO Qiu-hua, XU Yuan-ze. Advances in Rheology and Its Applications. New York: Science Press, 2005: 912−916.

[15]周宏伟, 谢和平, 左建平. 深部高地应力下岩石力学行为研究进展[J]. 力学进展, 2005, 35 (1) : 91−99.ZHOU Hong-wei, XIE He-ping, ZUO Jian-ping. Developments researches on mechanical behaviors of rocks under the condition of high ground pressure in the depths[J]. Advances in Mechanics,2005, 35(1): 91−99.

[16]蔡美峰, 乔兰, 于波, 等. 金川二矿区深部地应力测量及其分布规律研究[J]. 岩石力学与工程学报, 1999, 18(4): 414−418.CAI Mei-feng, QIAO Lan, YU Bo, et al. Results and analysis of in-situ stress measurement at deep position of No.2 mining area of Jinchuan nichkel mine[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(4): 414−418.