原子系综双模压缩叠加相干态的制备和性质

杨 雄,郭 裕, 邹红梅

(1. 湖南师范大学物理与信息科学学院，中国 长沙 410081;2.长沙理工大学物理与电子科学学院，中国 长沙 410114)

纠缠是量子力学最奇特的性质之一.随着对其研究的深入，人们逐渐发现了它在量子计算与量子通信方面的研究价值：作为量子信息最基本的载体，是实现量子稠密编码、量子密钥分布、量子隐形传态与量子信息存贮等量子工程的基本保证.人们已提出了许多制备两粒子和多粒子纠缠的方案，涉及光学系统[1]、核磁共振[2]、腔场量子动力学[3]和玻色-爱因斯坦凝聚体[4]等领域.而原子系综纠缠态的制备，由于其与电磁场的群集作用，使得它具有制备效率高、对腔的品质因素要求不是很高且有较好的消相干效应等特点，更由于其在量子信息存贮与转移中潜在的应用能力[5]，近年来无论是在理论上还是实验上都得到研究者的极大关注，制备原子系综之间的纠缠态，以及实现纠缠在原子系综和量子光场之间的转移已成为一个有趣的话题.

Parkins, Solano and Cirac(PSC)[6]提出了一个在一对分离的原子系综之间制备双模压缩态的计划，这对原子系综同时与一个环形光学腔及外激光场集聚的相互作用.在他们的计划中只考虑了原子腔场的稳态解.在本文中，当考虑原子与腔场的瞬时相互作用后，给出了一个利用PSC提出的模制备两原子系综之间的一类新的非经典态，即所谓双模压缩相干叠加态的计划.此外，还讨论了所制备态的非经典性质.结果表明，双模压缩相干叠加态具有更强的非经典性质.

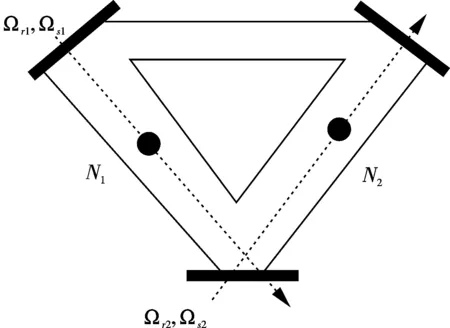
图1 通过一个环形腔制备两分离的原子系综纠缠相干态的设计图.原子系综1和2分别包含N1和N2个原子

1 双模压缩叠加相干态的制备

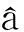
(1)

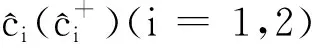
(2)

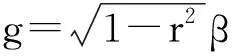
按照(2)式给出的有效哈密顿量，可以直接得到下面的幺正演化算符

U(τ)=Bac1(τ)Bbc2(τ),

(3)

这里我们引入一个时间标度τ = gt ，两个束分离器算符Bac1(τ)和 Bbc2(τ)为：

(4)

它将按以下形式与相干态作用

Bac1(τ)|α〉a|β〉c1=|αcosτ-iβsinτ〉a|βcosτ-iαsinτ〉c1,

Bbc2(τ)|α〉b|β〉c2=|αcosτ-iβsinτ〉b|βcosτ-iαsinτ〉c2,

(5)

设两个原子系综初始制备在双模压缩真空态|β〉c1|β〉c2，而腔场初始制备在如下式所示的相干态的叠加态：

|ψf(0)〉=M(α)(|α〉a+|-α〉a)⊗(|α〉b+|-α〉b),

(6)

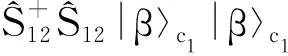
(7)

利用方程(5),即可得到系统在上述初始条件下τ刻的波函数为：

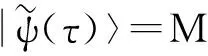
⊗|-αcosτ-iβsinτ〉b|βcosτ+iαsinτ〉c2+|αcosτ-iβsinτ〉b|βcosτ-iαsinτ〉c2,

(8)

而当τ=π/4时，便有

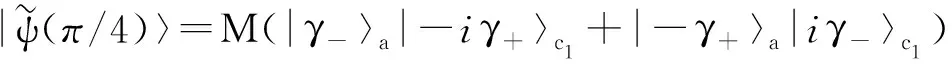
(9)

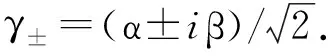
-C2[|φ-(α′)〉ab|φ-(iα′)〉c1c2+|ψ-(α′)〉ab|ψ-(iα′)〉c1c2],

(10)

这里的4个准-Bell态可以用双模压缩相干态|±α,±α〉和|±α,∓α〉定义如下：

|φ±(α)〉=N±(α)(|α,α〉±|-α,-α〉),

|ψ±(α)〉=N±(α)(|α,-α〉±|-α,α〉),

(11)

这里的正交归一化常数为

(12)

在方程(10)中的两个系数为

(13)

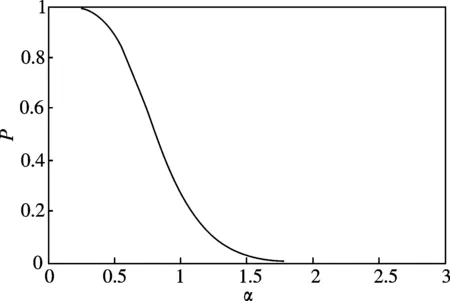
图2 由方程(14)给出的两个准Bell态|φ+(α)〉和|ψ+(α)〉间的交积作为相干辐度α的函数

方程(10)中的4个准-Bell态除以下情形外是正交的：

〈φ+(α)|ψ+(α)〉=cosh-1(2|α|2)

(14)

这说明4个准-Bell态当α→∞时是近似的Bell态.在图2中我们作出了|φ+(α)〉和|ψ+(α)〉两个准-Bell态的交积(即方程(14))随相干辐度α变化的曲线.从图2可见，方程(14)给出的交叠函数随相干辐度α的增加而迅速接近零.令我们感到有趣的是|φ-(α)〉和|ψ-(α)〉有一个ebit的纠缠，并与α无关；而|φ+(α)〉和|ψ+(α)〉只有在α→∞的极限下才是最大纠缠态.

对方程(10)中的两原子系综再一次实施双模压缩变换，系统的波涵数在式(1)所示的表象中变为如下形式：

|ψ(π/4)〉=S12C1[|φ+(α′)〉ab|φ+(iα′)〉c1c2+|ψ+(α′)〉ab|ψ+(iα′)〉c1c2]-

S12C2[|φ-(α′)〉ab|φ-(iα′)〉c1c2+|ψ-(α′)〉ab|ψ-(iα′)〉c1c2],

(15)

由方程(15)可见，在设定的初始条件下，系统在时刻τ=π/4的态是一个两原子系综和两腔场之间的四态纠缠态.这样的原子-光子纠缠态由两对原子双模压缩叠加相干态和两对光子准Bell态构成.由于光子的准Bell态|φ-(α′)〉ab(|ψ-(α′)〉ab)与其他3个光子准Bell态是正交的，经对光子准Bell态|φ-(α′)〉ab和|ψ-(α′)〉ab进行非局域的Bell测量，能获得下面给出的两原子系综之间的两个双模压缩相干叠加态：

(16)

它们也是一类非经典态，下面将证明，它们表现出比单个的双模压缩态更强的压缩效应和反聚束效应.方程(10)表明获得方程(16)的两个双模压缩叠加相干态的成功概率是相同的，由下式给出：

(17)

从方程(10)可以看到，通过对光子准Bell态|φ+(iα′)〉ab和|ψ+(iα′)〉ab进行非局域的Bell测量，也能近似获得另两个原子系综之间的准-Bell态：

(18)

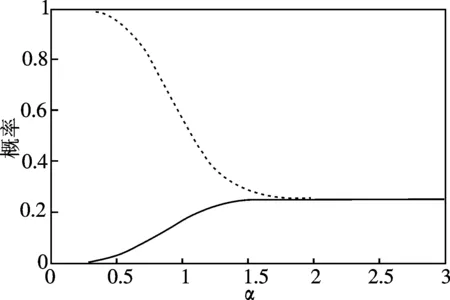
图3 制备双模压缩叠加相干态的成功概率作为相干辐度α的函数.实线与虚线分别与式(16)和(18)对应

式 (10) 表明获得方程(18)的两个态的成功概率是相同的，可由下面的表达式给出

(19)

在图3中，我们作出了成功概率作为相干辐度α的函数曲线.实线和虚线分别与方程(17)、(19)给出的成功概率相一致.从图3中可看到，在α <2的小相干振辐情形下，制备由方程(18)给出的准Bell态比制备方程(16)形式的准Bell态的成功概率要大.然而，在大相干辐度α>2情形下，制备(16)态和(18)态的成功概率是相同的.

2 双模压缩叠加相干态的非经典性质

首先研究双模标准压缩.根据文献[9]，可以定义两原子系综的双模正交分量为

(20)

通过计算可以得到态(16)的方差〈ΔX1〉2为

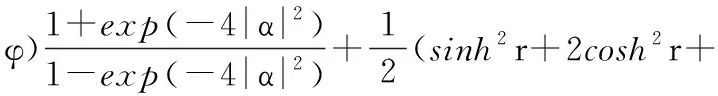
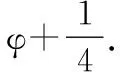
(21)

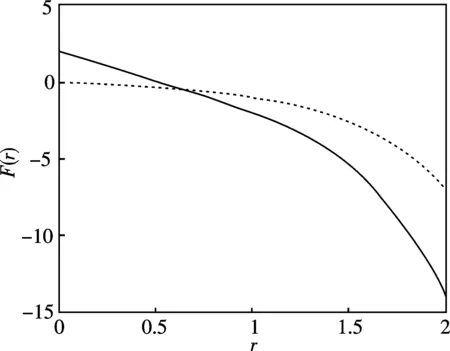
图4 当α=1时，F随压缩因子r变化的函数

接下来讨论亚泊松分布.我们利用Q参数解决这个问题[10].Q参数反映辐射场偏离经典场的程度.Q<1，光子呈亚泊松分布，光子出现反聚束效应，这是光场的非经典性质之一.可以类似的定义两模原子系综的Q参数为

(22)

经过计算，可得

sinh22r(α4+α2)-2sinh2rsinh2rcosφ(α4+2α2)+sinh4r(α4+4α2+2)]-

sinh22r(α4-α2)+2sinh2rsinh2rcosφ(α4-2α2)+

sinh4r(α4+4α2+2)]exp(-4α2).

(23)

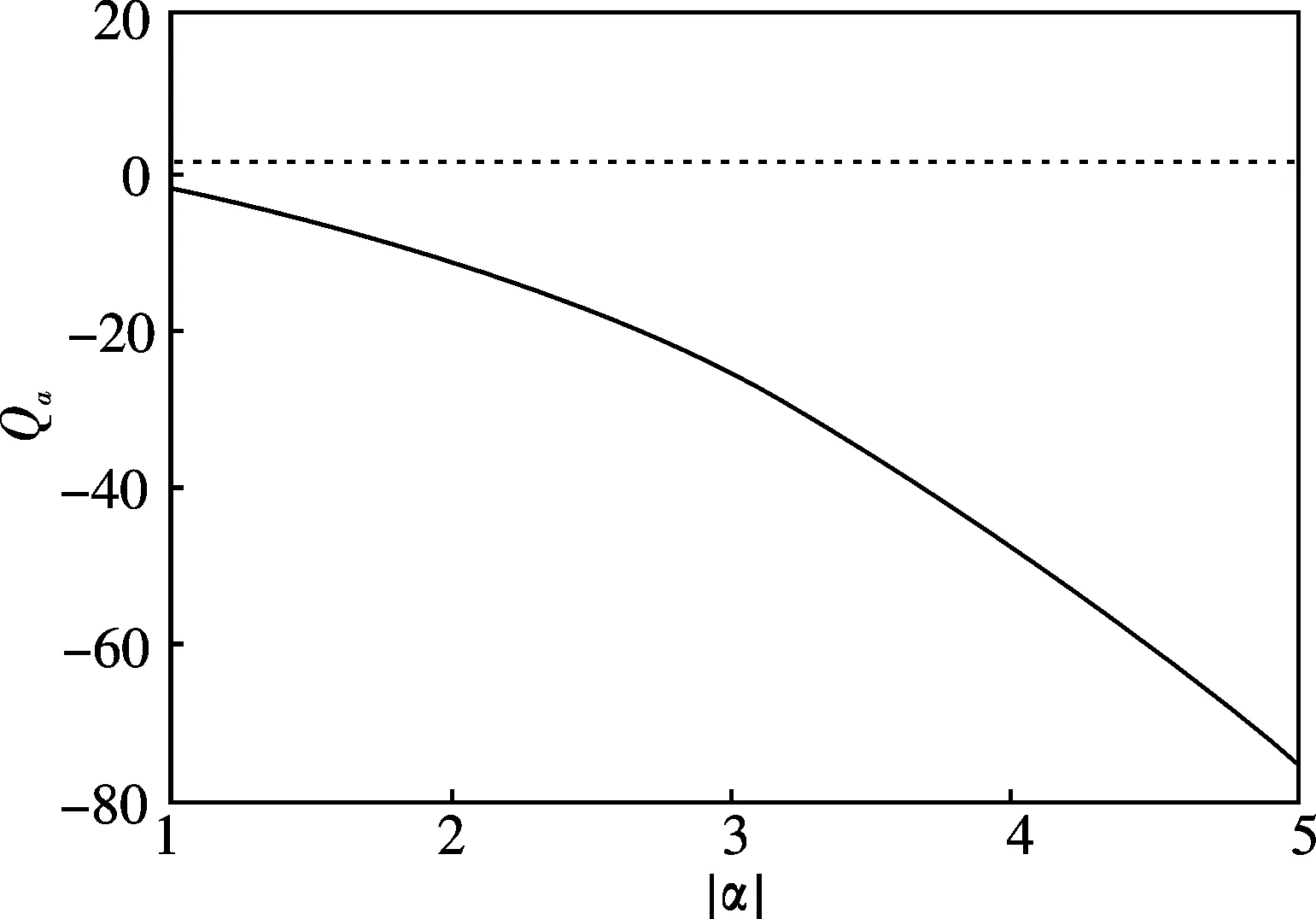
图5 当r=0.5时，Q参数随相干辐度变化α=1的函数

这样便能求得双模原子系综处于态(16)的Q参数.图5中的实线给出了模1的Q参数Q1随|α|2的变化关系(取r=0.5，φ =0), 而虚线反映了单个双模压缩相干态的这种关系.从图5可知，双模压缩叠加相干态的反聚束效应比单个的双模压缩相干态强得多.

同样地，数值计算表明，与态(16)相应的模间二阶相干度比，单个的双模压缩相干态大得多.总之，双模压缩相干叠加态具有更显著的非经典性质.

3 结论和实验实现

综上所述，已经阐明在一个环形腔设置中，如何利用原子系综和腔场之间的相互作用来制备两原子系综的双模压缩相干叠加态.通过对腔场进行准Bell态测量，可以精确地制备出两原子系综之间的两对准Bell态.还讨论了双模压缩相干叠加态的非经典性质.结论表明，双模压缩叠加相干态具有更强的非经典性质.需强调的是，为了获得两原子综间的纠缠态，我们不得不对腔场进行准Bell的测量.关于4个光学准Bell态的非局域测量，根据文献[11, 12]中提出的计划，通过使用束分离器，相移器，非线性Kerr介质，相干光源和光学检测器，能被任意的高精度完成.

参考文献：

[1] WALMSLEY A I， RAYMER M G. Toward quantum informaion processing with photons[J]. Science, 2005, 307:1 733-1 734.

[2] PENG X H, ZHU X W, FANG X M,etal. Experimental implementation of remote state preparation by magnetic resonance[J]. Phys Lett A, 2003, 306: 271-276.

[3] SONG K H. Preparation of many-type atomic entangled states via atom-cavityfield Raman interaction[J]. Acta Phys Sin, 2000, 49: 441-444.

[4] PU H, MEYSTRE P. Creating macroscopic atomic einstein-podolsky-rosen states from Bose-Einstein condenstes[J].Phys Rev Lett, 2000,85:3 987-3 990.

[5] 赵 晗，周小清，杨小琳.基于腔QED的多用户间的多原子量子信道的建立[J].物理学报，2009,58(9):5 970-5 977.

[6] PARKINS A S, SOLANO E, CIRAC J I. Unconditional two-mode squeezing of separated atomic ensembles[J]. Phys Rev Lett, 2006,96:053 602-053 605.

[8] HOLSTEIN T, PRIMAKOFF H. Field dependence of the intrinsic domain magnetization of a ferromagnet[J]. Phys Rev,1940,58:1 098-1 113.

[9] ABDEL-HAFEZ A M . Degenerate and nondegenerate two-mode normal squeezing in a two-level atom and two-mode system[J].Phys Rev A, 1992,45:6 610-6 614.

[10] MANDEL L. Sub-Poissonian photon statistcs in resonance fluorescence[J]. Opt Lett,1979,4: 205-207.

[11] VAN ENK S J, HIROTA O. Entangled coherent states: Teleportation and decoherence[J]. Phys Rev A,2001,64:022 313-022 318.

[12] JEONG1 H, KIM M S, LEE J. Quantum-information processing for a coherent superposition state via a mixedentangled coherent channel[J]. Phys Rev A, 2001,64:052 308-052 314.

[13] KRUSE D, RUDER M, BENHELM J,etal. Cold atoms in a high-Q ring cavity[J]. Phys Rev A,2003,67:051 802 (R)-051 805.

[14] NAGORNY B， ELSSSER T, RICHTER H,etal. Optical lattice in a high-finesse ring resonator[J].Phys Rev A,2003,67:031 401(R) -031 404.