系列涡轮钻具额定参数设计的对应等功率方法

冯 进，李雯锦，张慢来，张先勇

(长江大学机械工程学院，湖北 荆州 434023)

系列涡轮钻具额定参数设计的对应等功率方法

冯 进，李雯锦，张慢来，张先勇

(长江大学机械工程学院，湖北 荆州 434023)

根据涡轮钻具工作理论和机械钻速方程，分析了相关因素对机械钻速的影响。基于同尺寸系列涡轮钻具应具有同样机械钻速的观点，提出了额定参数设计的对应等功率准则，并建立了同尺寸系列涡轮钻具额定参数之间的对应关系。在钻头参数和岩石约束抗压强度一定的情况下，以许用最小机械钻速、钻头钻压范围、钻井工艺要求为依据，确定了上、下限额定参数，建立了同尺寸系列涡轮钻具额定参数设计的定量计算方法。该方法也可用于涡轮钻具的选择计算。

涡轮钻具；系列设计；等功率准则；额定参数；计算方法

涡轮钻具具有大功率、高转速、相对适中扭矩和大压降的特点，在高温、高压和高密度泥浆环境下不影响其工作性能，适合小的切削深度和高转速实现较高的机械钻速，特别适合硬地层和研磨性地层钻井，在高陡构造地层能实现防斜快打。涡轮钻具同心旋转，反扭矩小，工具面定向容易控制，钻井井眼规则。涡轮钻具的这些优势在相当长的时间里没有加以利用，其关键在于涡轮钻具的推力轴承寿命短，钻头的工作转速比较低，钻井设备能力普遍缺乏足够的水马力。上述因素导致涡轮钻具在前苏联以外的国家没有被广泛使用，仅用于定向造斜和短井段钻井。

近年来，随着科学技术的进步，石油钻井设备技术水平大幅提升，现代石油钻机普遍配备了高压大功率泥浆泵，满足了钻井新工艺、新技术的需要。新材料、新工艺在钻头和泥浆润滑推力轴承上的应用，使固定切削齿钻头的工作转速超过800～1500r/min[1]，抗高温、耐冲击、抗磨损的PDC推力轴承寿命已超过400～600h[2]。涡轮钻具动力性能不断改善，行程寿命大幅提高，在减少起下钻次数和提高机械钻速方面具有显著的优势[3]，应用范围不断扩大[4～6]，在井深、超深井钻井中涡轮钻具有广阔的应用前景。

涡轮钻具由涡轮节和支承节组成，涡轮节把液体的压能转变为涡轮轴上的机械能，支承节把涡轮轴上的机械能传递给钻头并承受来自钻头的反作用力。为了满足钻井的不同需要，涡轮钻具有不同尺寸规格，同尺寸规格中有不同系列，同系列中又有不同型号。对同尺寸系列涡轮钻具，其工作参数范围不同，用何种方法来确定合理的工作参数范围，这是值得研究的重要课题。对此笔者经过探究，提出了对应等功率准则，并建立了同尺寸系列涡轮钻具额定参数设计的计算方法。

1 涡轮钻具的机械性能

涡轮钻具实质上是叶片式泥浆马达，其通过涡轮定子叶片和转子叶片改变液体的流动方向，基于动量矩原理把液体的压能转变为机械能，通过涡轮轴输出转速和扭矩，带动钻头破岩。涡轮钻具输出参数有转速n、扭矩T和输出功率N，输入参数有流量Q、压降Δp和输入功率Ni，效率η为输出功率与输入功率的之比。涡轮钻具的机械性能涉及到在流量Q一定时，转速与其他参数间的关系，其中转速与扭矩T和输出功率N的关系[7]为：

(1)

(2)

式中，Tmax为涡轮钻具的制动扭矩，N·m，与泥浆密度、涡轮的几何尺寸和叶栅叶型水力性能以及工作流量有关；nmax为涡轮输出轴最大转速，r/min，随流量变化而变化。

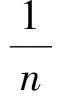
(3)

2 对应等功率的依据

无论采用何种驱动方式钻井，机械钻速是需要考虑的主要因素。在旋转法破岩过程中，必须给钻头施加一定的钻压，才能使钻头的切削齿压入岩石一定深度(切削深度)；提供一定的扭矩，才能克服破岩时摩擦和剪切产生的反力矩；有一定的切削速度(转速)，才能得到一定的机械钻速。因此，分析影响机械钻速和涡轮钻具输出参数的相关因素，对涡轮钻具设计非常重要。

Pessier等[8,9]根据机械比能原理，建立了与所钻地层的岩石力学性能(抗压强度)、钻头直径、钻压、钻头机械效率等因素有关的机械比能关系，即：

(4)

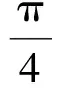
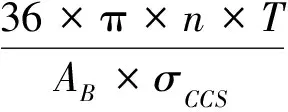
(5)

将式(5)除以转速n，得切削深度S(单位mm/ r)，即：

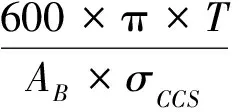
(6)

扭矩T是钻头破岩时岩石对钻头的反作用力矩，其是关于钻压、钻头几何参数、岩石力学性能的函数，在数值上等于涡轮钻具提供给钻头的驱动力矩。扭矩T用下式计算：

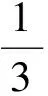
(7)

式中，μ表示滑动摩擦系数，通过试验确定。针对PDC钻头可用下式计算μ[12]：

μ=0.9402×φρ×exp(-1.161×10-9σCCS)

(8)

式中，φρ是泥浆密度对滑动摩擦系数的影响系数：

φρ=2.9982-0.8876ln(8.347×10-3×ρ)

(9)

式中，ρ为泥浆密度，kg/m3。

在相同钻头和地层岩性下，由式(5)可以看出，随机械功率增加，机械钻速上升，只要转速与扭矩的乘积不变，机械钻速就相等；由式(6)和式(7)可以看出，钻压大，扭矩和切削深度也大。在同尺寸的系列涡轮钻具中，在相同钻头和地层岩性下，每一型号的涡轮钻具必须有能力达到同样的机械钻速，才能有相同的竞争力。基于上述观点，笔者认为同尺寸系列涡轮钻具应具有相同的输出功率范围，在各自的输出功率范围内都存在对应的等输出功率点，这就是对应等功率设计准则。

涡轮钻具的性能特点是随排量大增加，转速、扭矩、压降、输出功率和输入功率也随之增大。同尺寸系列涡轮钻具应满足在一定流量范围内工作的要求，既有对应较大流量、较低压降的涡轮钻具，也有对应较小流量、较高压降的涡轮钻具。涡轮钻具的能量由泥浆泵提供，而泥浆泵的输入功率是一定的。排量大时泥浆泵的额定压力低，排量小时泥浆泵的额定压力高。可见，对应等功率设计准则与同尺寸系列涡轮钻具工作需要和泥浆泵的性能特点是一致的。

3 对应额定参数的关系

为说明对应等功率设计原理，设同尺寸系列涡轮钻具有3个型号，分别用下标1、2、3表示，下标U和L分别表示涡轮钻具的对应上、下限额定参数，在工作介质物性不变的情况下研究同尺寸系列涡轮钻具的额定参数关系。根据对应等功率设计准则，涡轮钻具的下限功率NL和上限功率NU满足：

N1L=N2L=N3L=NL

(10)

N1U=N2U=N3U=NU

(11)

3.1上、下限流量

若涡轮钻具1、2、3的下限流量分别为Q1L、Q2L和Q3L，上限流量分别为Q1U、Q2U和Q3U，根据式(3)和式(10)求上限功率，结果代入式(11)中，得：

简化整理为：

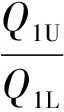
(12)

为了保证流量分布合理，取优先系数k=1.06～1.25，即：

Q1L=k×Q2LQ2L=k×Q3LQ1U=k×Q2UQ2U=k×Q3U

(13)

若已知Q1U和Q3L，由式(13)得：

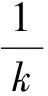
(14)

将式(14)代入式(12)，得：

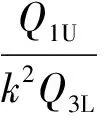
(15)

3.2上、下限转速

若涡轮钻具1、2、3的下限转速分别为n1L、n2L和n3L，上限转速分别为n1U、n2U和n3U，根据式(3)和式(12)，得：

(16)

为了保证下限转速分布合理，取优先系数k=1.06～1.25，即：

n1L=kn2Ln2L=kn3L

(17)

在已知n1L时，由式(17)得：

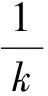
(18)

根据式(16)，得：

n1U=n1L×Cn2U=n2L×Cn3U=n3L×C

(19)

3.3上、下限输出功率

若涡轮钻具1的下限扭矩T1L已知，则下限功率NL为：

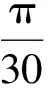
(20)

根据式(3)，上限功率NU为：

(21)

3.4上、下限扭矩

涡轮钻具的输出功率为涡轮轴角速度与输出扭矩的乘积，在已知转速、输出功率时，可求扭矩。若涡轮钻具1、2、3的下限转速分别为T1L、T2L、T3L，上限转速分别为T1U、T2U、T3U，根据式(20)～(21)，可计算其上、下限扭矩，即：

(22)

(23)

3.5上、下限压降

设涡轮钻具1、2、3的效率分别为η1、η2、η3，下限压降分别为Δp1L、Δp2L、Δp3L，上限压降分别为Δp1U、Δp2U、Δp3U，其上、下限压降由下式确定：

(24)

(25)

4 额定参数的确定

在建立同尺寸系列涡轮钻具额定参数计算关系时，假设下限扭矩T1L和下限转速n1L为已知。因此，必须建立T1L和n1L的计算方法。对于钻井而言，希望通过提高机械钻速降低钻井成本。从经济性上讲，总存在一个可接受的机械钻速下限值(ROP)L。根据钻井工艺，在已知钻头尺寸和岩石的力学性能的条件下，为了有效地发挥涡轮钻具和钻头的破岩作用，必须给钻头施加适当的钻压。在钻头许用钻压下限值WB min附近取钻压WB1L，由式(7)计算WB1所对应扭矩TB1L。因n1Lgt;n2Lgt;n3L，所以涡轮钻具1对应的下限额定扭矩T1L=TB1L，此时，可由式(4)计算n1L。

某一尺寸规格的涡轮钻具对应有适合的钻头尺寸范围，钻井工艺对不同井眼直径的泥浆上返速度有一定要求，由此可以确定Q3L和Q1U。这样，可以计算同尺寸相似系列涡轮钻具上、下限额定参数。最后，由式(7)计算涡轮钻具适合的钻压范围，即WB1L、WB1U、WB2L、WB2U、WB3L和WB3U。

5 结 语

通过涡轮钻具工作理论和机械钻速方程，阐述了同尺寸系列涡轮钻具有能力达到相同机械钻速的观点，提出了涡轮钻具额定参数设计的对应等功率准则。基于对应等功率准则，建立了同尺寸系列涡轮钻具额定参数之间的关系。在钻头参数和岩石约束抗压强度一定的情况下，以许用最小机械钻速、钻头钻压范围、钻井工艺要求为依据，确定上、下限额定参数，建立了同尺寸系列涡轮钻具额定参数设计的定量计算方法。基于对应等功率的同尺寸系列涡轮钻具额定参数设计方法，将地层、钻头、涡轮钻具、钻井工艺和机械钻速有机地结合起来，体系比较完善，定量计算方便。该方法也可用于涡轮钻具的选择计算。

[1]Beaton T, Seale R. Applications and Case Histories of Geared Turbodrilling in the North Sea[J]. IADC/SPE 87970,2004.

[2]Sexton T N, Cooley C H. Polycrystalline diamond thrust bearings for down-hole oil and gas drilling tools[J].Proceedings of 17th International Conference on Wear of Materials, Las Vegas, USA April， 2009.

[3] Calnand D, Seale R, Beaton T. Identifying Applications for Turbodrilling and Evaluating Historical Performances in North America[J].PETSOC2004-208, 2004.

[4] Seale R, Beaton T, Flint G. Optimizing Turbodrill Designs for Coiled Tubing Applications[J]. SPE 91453, 2004.

[5] Beaton T, Seale R. The Use of Turbodrills in Coiled Tubing Applications[J]. SPE 89343, 2004.

[6] Grigor C, Conroy D, Henderson M. Expanding the Use of Turbodrills in Coiled Tubing and Workover Applications[J]. SPE113721, 2008.

[7] 万邦烈, 李继志. 石油工程流体机械[M]. 北京：石油工业出版社,2010.

[8] Pessier R C, Fear M J. Quantifying Common Drilling Problems With Mechanical Specific Energy and a Bit-Specific Coefficient of Sliding Friction[J]. SPE24584, 1992.

[9] Armenta M. Identifying Inefficient Drilling Conditions Using Drilling-Specific Energy[J]. SPE116667, 2008.

[10] Dupriest F E, Koederitz W L. Maximizing Drill Rates with Real-Time Surveillance of Mechanical Specific Energy[J].SPE92194,2005.

[11] Robert J, John V, Ross A. Real-Time Specific Energy Monitoring Reveals Drilling Inefficiency and Enhances the Understanding of When to Pull Worn PDC Bits[J]. SPE74520, 2002.

[12] Hector U, Caicedo, William M,etal.Unique ROP Predictor Using Bit-specific Coefficient of Sliding Friction and Mechanical Efficiency as a Function of Confined Compressive Strength Impacts Drilling Performance[J].SPE92576, 2005.

[编辑] 李启栋

TE921

A

1673-1409(2010)03-N047-04

2010-05-26

冯进(1958-)男，1997年大学毕业，博士，教授，现主要从事流体机械与工程方面的教学与研究工作。