阵列涡流传感器互感信息三维有限元仿真

何永勃，邵雨果

（中国民航大学航空自动化学院，天津 300300）

电涡流传感器阵列测试技术的研究始于20世纪80年代中期，采用电子学方法，对阵列单元分时切换，完成一个阵列的巡回检测，其一次检测过程相当于传统单个探头的步进扫描过程，可实现大面积范围的高速测量，能够达到与单个传感器相同的测量精度和分辨率，可有效提高传感器的测试速度、测量精度和可靠性[1]，已在很多领域得到应用。近年来，阵列电涡流传感器技术得到极大发展。徐可北教授阐述了一种内通过式阵列涡流探头，采用不同的激励—接收组合方式，实现管材轴向和周向缺陷的检测[2]。A.Zaoui等人研究了当裂纹为理想裂纹时，对阵列涡流中相邻两线圈分别施加相同和相反方向电流，获得各线圈的阻抗变化规律[3]。阵列式传感器的研究成为当前传感器技术研究中的重要内容和发展方向。

当前，阵列涡流传感器多为多个独立线圈的简单组合，对线圈之间的互感信息研究报道较少。本文设计了阵列涡流传感器模型，利用有限元方法，研究了放置于平板导体上阵列探头线圈之间的互感作用，仿真结果直观显示了裂纹对涡流的影响，获取了比单探头更多的缺陷信息，较为精确地测量涡流区域内裂纹大小和位置。提高了检测精度和灵敏度。

1 基本原理

电涡流线圈阵列结构形式的设计灵活多变，可以在基底材料上制作多个敏感线圈，布置成矩形阵列形式（3×3）。依次给线圈施加正弦交流激励，将激励线圈周围的其它线圈作为接收线圈，利用激励线圈与检测线圈之间的互感作用，能够收集到更多涡流检测信息，从而判断缺陷特征，更加真实地反映导电工件的实际状况。

当线圈阵列为 3×3 时（ 图 1（ a）），处于中心的水平方向裂纹对左右1、3号线圈影响较大，而对5、8号线圈和四周4、6、7、9号线圈影响较小，并且阵列线圈对称分布，可以将其中的三个线圈作为研究模型，如图1（b）所示。被检测平板（铝板）上方从左到右均匀排布着3个参数（匝数、内外径、高度等）完全一致涡流探头线圈，其中，中间位置2号线圈为激励线圈和检测线圈合二为一，施加正弦交流激励，1、3号线圈为检测线圈。

图1 阵列涡流传感器检测模型Fig.1 Model of eddy current sensor array

当2号线圈施加正弦交流电激励信号时，由于涡流效应，被检工件表面产生涡流，此涡流产生一个磁场，激励线圈和涡流产生磁场的叠加使得检测线圈1、3的磁通量发生变化，产生感应电动势。在理想情况下，忽略线圈直流电阻，感应电动势用向量法表示如下

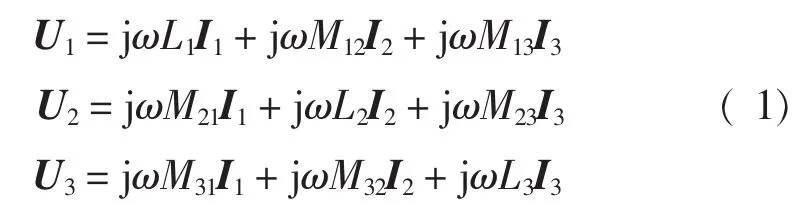
由于检测线圈为开路情况，则Ⅰ1，Ⅰ3数值都为0，因此，检测线圈的感应电动势能够反映线圈2对线圈1、3的互感值M12和M32。当被检测工件表面或近表面存在缺陷时，涡流分布发生畸变，导致涡流产生的磁场变化，使得线圈之间互感作用相应地发生改变，而式（1）说明感应电动势能够反映线圈间的互感。因此，可以根据检测线圈感应电动势的变化判断线圈间的互感，进而推断被检测工件是否存在缺陷及其大小和位置等。互感信息增加了测量数据，可用于进一步的图像重建工作，提高图像分辨率。本文采用有限元仿真的方法，对同一深度不同长度的裂纹进行了三维仿真，显示了相应的涡流场分布，得到了检测线圈的感应电动势幅值和相位变化情况。

2 有限元仿真模型

2.1 模型参数的设计

另外，当被检测平板直径与线圈直径比例大于5且金属板厚度与集肤深度比例大于4时，可以认为金属平板对线圈阻抗的影响与无穷大平板一致。被检测工件为非导磁性材料铝板，尺寸为50 mm×50 mm×10 mm，电阻率为 2.65×10-8Ω·m，相对磁导率为 1。

2.2 激励频率的选取

试验频率的选取与工件的特征频率fg密切相关，可以将工件看成半无限大平面，建立涡流简化模型，利用涡流环理论推导出特征频率的计算公式（2）[5]，特征频率只与线圈外径和被检测导体电导率和磁导率有关。

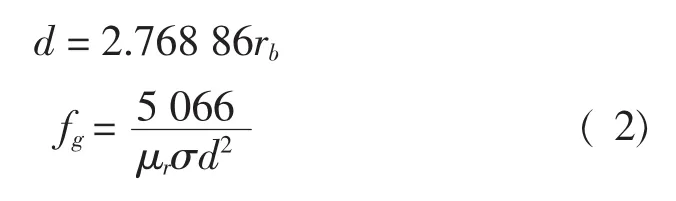
其中：rb为线圈外半径；μr、σ分别为被检测导体相对磁导率和电导率。

在放置式线圈检测工件表面裂纹时，其工作频率一般选取f=（10～50）fg。本文在仿真时，选取频率为10 kHz。

3 仿真结果与分析

当场点深度为标准渗透深度δ的2倍时，涡流幅值衰减为表面处的1/10，因此涡流探头的有效探测深度大致是2δ，裂纹深度的设计需要依据于涡流探头的有效探测深度。根据阵列探头线圈外直径的大小，可以将裂纹分为长裂纹和短裂纹，长裂纹的长度L大于等于线圈外直径，短裂纹的长度L小于线圈外直径。本文研究了同一深度下三种不同长度裂纹的情况，裂纹尺寸（长×宽×深）是：18 mm×1 mm×1.8 mm，10 mm×1 mm×1.8 mm，4 mm×1 mm×1.8 mm。

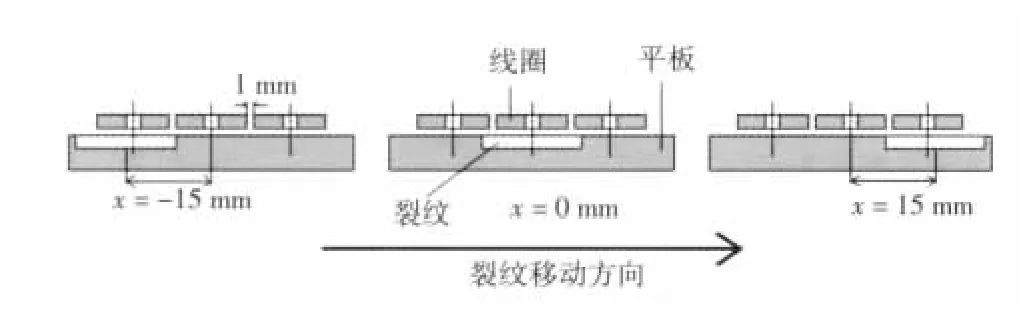
图2 裂纹移动方向示意图Fig.2 Schematic of direction of crack positions

3.1 线圈感应电动势幅值的变化

当裂纹按图2所示的方向相对移动时，各线圈感应电动势随之发生变化。2号线圈感应电动势幅值变化曲线如图3所示。当裂纹为长裂纹（裂纹长度L=18，10）时，裂纹移动到图2中间位置即2号线圈正下方时感应电动势达到最大值，此时线圈产生的全部涡流都与裂纹相互作用（图4（c）），与平板不存在裂纹时的涡流（图4（a））比较，裂纹的存在导致涡流的阻断，当裂纹足够长时，会在裂纹的两侧各自形成一个涡流环。在裂纹移动中，感应电动势幅值曲线两侧各出现“肩”的形状，分别对应于裂纹的前端进入激励线圈空芯部位和裂纹的后端离开激励线圈空芯部位。裂纹为短裂纹（L=4）时，线圈感应电动势幅值曲线出现两个峰值，分别为裂纹中心与线圈平均半径Rave大约重合，当短裂纹中心位于激励线圈正下方时，对应曲线的凹谷，此时空芯区域的涡流较弱，短裂纹相对整个涡流环的影响较小[6]。

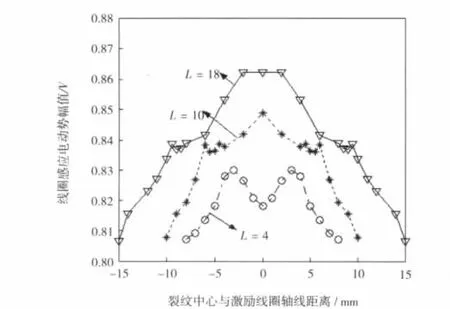
图3 裂纹相对移动时2号线圈感应电动势幅值变化曲线Fig.3 Induced potential amplitude variation of no.2 coil with respect to positions of cracks

图4 不同位置裂纹对涡流的影响Fig.4 Eddy current with different positions of crack

1号线圈与3号线圈相对对称，在裂纹移动过程中，与3号的变化趋势相反。图5曲线显示，随着裂纹移动逐渐靠近3号线圈，3号线圈感应电动势幅值会急剧增大，但增大到一定程度，又会突然下降。当裂纹为长裂纹（裂纹长度L=18，10）时，在裂纹前端越过激励线圈空芯区域前，曲线变化相对平缓，此时裂纹基本没有影响到右侧涡流，对3号线圈的磁通量影响较小。并且空芯区域涡流比较弱，影响变化不大。裂纹前端越过空芯区域后，曲线迅速上升，此时右侧涡流绕过裂纹前端，涡流向外侧流动（图4（b）），涡流密度集中在前端边缘位置，裂纹影响了整个涡流环，相当于裂纹与激励线圈左右两侧的绕组都发生作用。而当裂纹后端离开空芯区域后曲线急剧下降，此时裂纹只影响右侧涡流，相当于裂纹只与激励线圈右侧绕组发生作用，涡流流动方向如（图4（d）），涡流向裂纹后端左侧偏移。裂纹为短裂纹（L=4）时，当裂纹前端大约越过－Rave后曲线迅速上升，当裂纹后端大约离开Rave后曲线急剧下降。

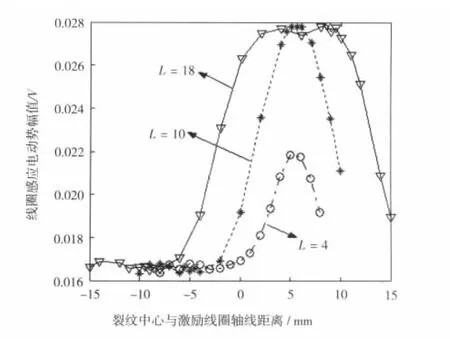
图5 裂纹相对移动时3号线圈感应电动势幅值变化曲线Fig.5 Induced potential amplitude variation of no.3 coil with respect to positions of cracks

在裂纹按图3方向移动过程中，也可以观察1号和3号线圈感应电动势的幅值之差，图6给出了幅值差变化曲线。当裂纹中心位于2号线圈正下方时，模型左右完全对称，1号和3号的感应电动势幅值差为0。长裂纹的前端进入空芯区域时达到最大值，其后端离开空芯区域时达到最小值；对短裂纹而言，其前端与－Rave重合时达到最大值，其后端与Rave重合时达到最小值。

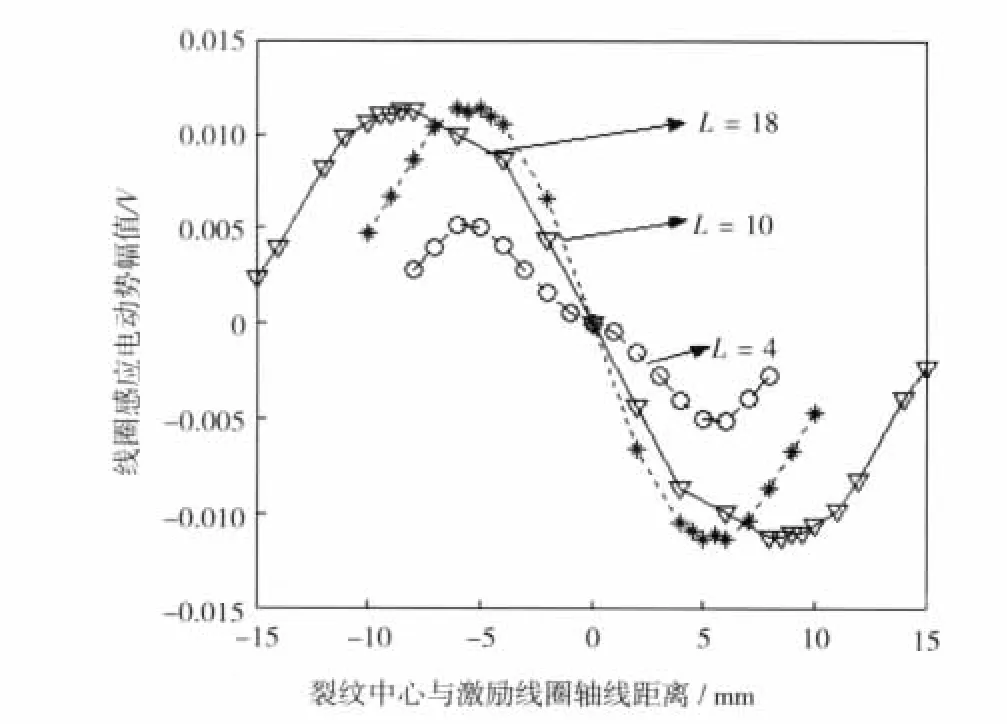
图6 裂纹相对移动时1号和3号线圈感应电动势幅值差变化曲线Fig.6 Difference between no.1 and no.3 coil induced potential amplitudes with respect to positions of the cracks

3.2 线圈感应电动势相位的变化

裂纹相对移动过程中，2号线圈的相位基本保持不变，当裂纹长度改变时相位的变化量也特别小。3号线圈的相位变化曲线与其幅值变化曲线大体一致，如图7所示，曲线变化过程中存在最大值。对长裂纹来说，最大值出现在裂纹后端离开2号线圈空芯区域部分，而对于短裂纹，最大值出现在裂纹后端离开平均半径Rave时。

4 结语

本文通过ANSYS有限元仿真模拟了裂纹相对于线圈移动时对涡流的影响，并得到了在同一深度不同长度裂纹下阵列传感器中各线圈的感应电动势幅值和相位变化曲线，以此表现线圈间的互感作用，反映更多有用的缺陷信息。仿真结果表明，裂纹在不同位置时会导致阵列检测线圈感应电动势发生变化，并且呈现一定的特征。因此，可以根据检测线圈感应电动势的相对大小判断缺陷信息，证明利用阵列线圈之间的互感判断裂纹大小和位置等信息是可行的，并且仿真结果为后续的图像重建工作提供了经验依据。此外，本文只是研究了3个线圈的情况，还可以在激励线圈周围放置更多的检测线圈，收集更多有用缺陷信息，从而判断缺陷特征。

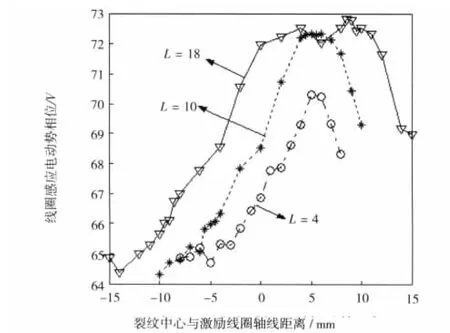
图7 裂纹相对移动时3号线圈感应电动势相位变化曲线Fig.7 Curves of induced potential phase variation of no.3 coil with respect to positions of cracks

[1]丁天怀，陈祥林.电涡流传感器阵列测试技术[J].测试技术学报，2006，20（ 1）：1-5.

[2]徐可北.涡流阵列检测技术[J].冶金分析，2004（z2）：645-647.

[3]A ZAOUI，H MENANA，M FELIACHI， et al.Generalization of the ideal crack model for an arrayed eddy current sensor[J].IEEE Transactions on Magnetics，2008，44（ 6）：1638-1641.

[4]王 鹏，丁天怀，付志斌.平面电涡流线圈的结构参数设计[J].清华大学学报（ 自然科学版），2007，47（ 11）：1959-1961.

[5]孙金立，陈新波.放置式探头检测工件时特征频率的计算[J].无损检测，2001，23（ 5）：185-189.

[6]陈德智，邵可然，王 涛.蒸汽发生器管道涡流检测Benchmark模型的数值计算[J].无损检测，2000，22（ 10）：435-438.