基于PBIL的综合QoS参数组播路由*

陈建明

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

基于PBIL的综合QoS参数组播路由*

陈建明

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

提出了一种基于PBIL(Population-Based Incremental Learning)的QoS组播路由算法，它能在综合QoS参数约束条件下寻找代价最小的多播树.该算法有效地结合了遗传算法的进化特性与竞争学习算法的特点，采用基于路径的树编码结构和基于概率的备选路径集，在网络规模较大的情况下也能得到很好的应用.仿真实验表明,该算法快速有效.

Steiner树；QoS；组播；遗传算法；PBIL算法

0引言

QoS组播路由技术是网络多媒体信息传输的关键技术之一， 亦已有不少研究成果[1-2].理想的路由算法应在满足QoS的前提下实现路由代价最小.目前,学界对于多播路由问题已经提出了多种算法，总体目标是极小化构造的多播树代价.通常具有最小代价的多播树称为Steiner树[3]，该问题已证明是NP完全问题[4].传统的解决Steiner问题的启发式算法,能够在贪婪搜索的基础上,在多项式时间内找到合适的解(不是全局最优解)，其基本原理是对于搜索过程中遇到的每一个新状态，按估价函数计算出它的最佳代价估计值，然后选出当时估计值的最小状态，并从该节点开始搜索.该算法的计算速度慢，缺乏全局观点，而且可扩展性差，难以适应有动态成员的大型群组.

遗传算法作为一种智能优化方法,具有并行搜索、群体寻优的特点，适用于在复杂而庞大的搜索空间中寻找最优解或次优解，已广泛用于解决各种具有NP难度的问题.但是，已有实践表明,遗传算法在实际的重组操作过程中可能会破坏个体的构造块,从而产生连锁问题，导致算法逼近局部最优或者早熟[4].

Baluja在1994年提出了基于群体的增量学习(Population-Based Increased Learning，简称PBIL)算法[5]，该算法集成了基于函数优化的遗传搜索和竞争学习2种策略，将进化过程视为学习过程，通过竞争学习获取的知识——学习概率(Learning Probability)指导后代的产生.这种概率是整个进化过程的信息积累，同遗传算法的双亲基因重组相比，用它指导产生的后代将会更优生，因此能获得较快的收敛速度和理想的计算结果，已在实际问题中得到应用[6-7].

本文提出了一种基于PBIL算法的综合QoS参数组播路由算法，该算法编码简单，易于实施，实验结果也表明该算法是有效的.

1QoS组播路由模型

QoS是衡量通信网络的主要指标，它包括网络的费用、距离、带宽、时延、时延抖动、差错率、分组丢失率及安全等.通常，路由选择策略因网络可用资源状况和它本身对QoS要求的不同而异.针对不同的QoS要求，目前的算法主要侧重于带宽、时延、时延抖动、分组丢失率等等QoS参数约束的某个或某几个方面，适用面较窄.为了寻找能较好地适应QoS变化的路由算法，本文借鉴了邹阳等[8]提出的单点路由选择的数学模型，给出了综合QoS参数的组播路由模型.

在研究路由问题时，计算机网络可表示成一个无向赋权图G(V，E)，其中V表示节点集，E表示连接节点的通信链路集.对任意e∈E,设e的权值为w(w1,w2,…，wn)，其中wi(1≤i≤n)∈R是权的第i个分量的值.

在定义限制函数之前,先定义一个辅助函数:Boolean(表达式),当表达式的值为真时,其值为1;当表达式的值为假时,其值为0.

其中:m≤n;p1,p2,…,pr为无向赋权图G中的一条路径;Uk∈{w1,w2,…,wn}为权的某个分量;Uk(pj)为边pj的权的Uk分量的值;vk∈R，1≤k≤m.

限制函数L给出了QoS的一组约束，限制所搜寻的路径上的某些指标,如延时、距离等不超过某一上限.一般情况下，限制函数由路由器根据通信任务需要、网络当前资源状况以及网络状态给出.

考虑一个网络G〈V,E〉，组播源点s∈V,组播终点集D⊆{V-{s}}，N为组播终点集D的大小.T(s,D)表示从源节点s到终点集D的一颗组播树，Li是一条从源节点s到第i个终点的路径，1≤i≤N.QoS参数路由可以归结为发现一组从s到D的路径集T，并且T满足如下2个约束：

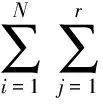
2QoS组播路由的PBIL算法

2.1 PBIL算法及其扩展

设s代表解的二进制编码，其长度为N，第i个基因位si(1≤i≤N)的取值为0或1；p=(p1,p2,…,pN)代表一个N维的概率向量，向量中各分量表示当前种群中的个体在对应基因位上不同取值时的学习概率；对于二进制编码的情况，pi(1≤i≤N)代表第i个基因位si取值为1时的学习概率；r是算法的学习速率;PM是变异率，染色体按PM概率随机选择部分pi进行调整;rm是变异速率;M是种群规模.初始概率向量iniP中学习概率pi的大小都为0.5，即各基因位上取值为0或1的机会均等.

标准PBIL算法的处理流程如下：

/* Initialize Probability VectorP*/

for (i=1;ilt;=N;i++)pi=0.5;

while(Not Termination Condition)

{

/* Sampling and Evaluation */

for (i=1;ilt;=M;i++)

{

Individual [i]=Sample (P);

Fitness [i]=Evaluate(Individual [i])

}

BestIndividual=FindBestIndividual (Fitness);

/* RevisePtowards BestIndividual*/

for (i=1;ilt;=N;i++)

pi=pi*(1.0-r)+BestIndividual*r;

/* Mutate Probability Vector */

for (i=1;ilt;=N;i++)

if (Random(0,1)lt;PM)

{

pi=pi*(1.0-rm)+Random(0 or 1) *rm;

}

}

为了适应任意整数编码，文献[7]对二进制PBIL算法进行了扩展，本文则在此基础上对算法进行了改进：保留进化和学习过程中产生的最优个体，用最优个体来修正学习概率，并利用它产生新的个体.改进后的整数编码的PBIL算法如下:

/* Initialize Probability VectorP*/

for (i=1;ilt;=N;i++)

for (j=1;jlt;=L;j++)

pij=1/L;

while(Not Termination Condition)

{

/* Sampling and Evaluation */

for (i=1;ilt;=M;i++)

{

Individual [i]=Sample (P);

Fitness [i]=Evaluate(Individual [i])

}

BestIndividual=FindBestIndividual (Fitness);

BestEver=(BestEvergt;BestIndividual?BestEver:BestIndividual);

/* RevisePtowards BestEver*/

for (i=1;ilt;=N;i++)

piB=piB+ε(B:bestEver);

/* Mutate Probability Vector */

for(i=1;ilt;=N;i++)

if (Random(0,1)lt;PM)

{

piB=piB*(1.0-rm)+Random(0 or 1) *rm;

}

}

其中:ε为修正常数;BestEver为到当前代为止的最优个体;其他符号与标准PBIL算法表的意义相同.

2.2 编 码

在利用PBIL算法求解QoS组播路由问题中，如何将问题的解转换为编码表达的染色体是PBIL算法的关键问题.文献[4]采用了一维二进制编码机制，这种编码模式使得算法编码、解码过程复杂, 并且算法的搜索空间随网络规模的增大而急剧增大，算法效率很低.为克服编码操作带来的负面影响,本文采用整数编码的方式,在该算法中，给定一个源节点s和一组目的节点D={d1,d2,…，dm}，PBIL算法的染色体可由长度为m的整数队列组成，染色体的基因是s和di之间的路径集Qi={p1i,p2i,…,pji,…,pki}中的路径.其中:pji为目的为i的第j条路由;k为s和di之间的路径数，群体中的每个染色体代表一棵多播树.由于每个节点所对应的路径集中的路径(根据前N条最短路进算法[9])可能有重复，而且重复的次数不一样，因此为便于后面的算法实施，对用前N条短路径算法[9]所求得的路径,根据概率进行选取,并填充到Qi，使|Qi|=L，1≤i≤|D|，即所有路径集的大小相同，L的大小根据具体情况而定.

因此，PBIL算法的染色体可由一系列整数队列组成，即基于路径表示的编码方法，该方法既减少了编码空间，也省略了解码操作.染色体、基因和路径的关系如图1 所示.

2.3 初始群体的选择

群体中的每个染色体代表一棵组播树.首先，对于每个目的节点d∈D，利用前N条最短路径算法[9]找出源节点s到d的所有满足限制函数L的路径，根据概率进行选取填充到Qi，组成路径集，作为PBIL算法编码空间的备选路径集.然后分别从每个路径集Qi中随机选一条路由组成一棵组播树,作为初始群体的染色体.种群规模M根据具体情况由系统设定.

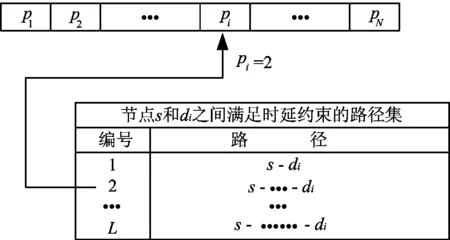
图1 染色体的表示

2.4 适应度函数

PBIL算法在进化搜索中基本不利用外部信息，仅以适应度函数为依据，利用种群中每个个体的适应度值进行搜索，适应度函数直接影响到PBIL算法的收敛速度以及能否找到最优解.因此，适应度函数应能反映被选个体的性能：性能好(满足综合QoS参数约束)的个体适应度大, 性能差(不满足QoS 约束或费用较大)的个体适应度小.本算法的适应度函数定义为

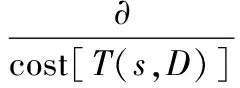
其中，∂是正实系数，对于组播树中的相同链路，其链路费用只计算1次.

2.5 变异操作

变异操作是一种基本操作，它在染色体上自发地产生随机的变化.在PBIL算法中，变异操作可以提供初始种群中不含有的基因，或找回选择过程中丢失的基因，为种群提供新的内容.变异操作以一个较小的随机概率改变个体字符串上的某些位，与种群的大小无关.变异操作本身是一种局部随机搜索，使PBIL算法具有局部的随机搜索能力；同时使得PBIL算法保持种群的多样性，以防止出现非成熟收敛.本文中，变异操作采用基本位变异[10]的方法，以变异概率PM随机指定的某一位或某几位基因位上的基因值随机地选择相应的路径集Qi中一个新的值进行替换.

2.6 进化程度的度量

基本PBIL 算法的终止条件是根据经验直接规定一个最大进化代数，这是进化计算中最简单也是最常用的方法.但是对于不同类型和不同规模的问题而言，算法的收敛速度存在极大的差异，单凭经验很难确定合理的最大代数，更无法确切地判断算法进化的程度.通过对PBIL 算法进化过程的分析可知，随着进化程度的逐步深入，各基因位上学习概率的大小从相同的初始值分别向0或1逼近.因此，衡量算法进化程度等同于衡量各基因位上学习概率的分散程度，这就启发我们可以根据进化过程中各基因位上学习概率的取值变化来定量地评价算法当前进化的程度.

目前已有学者[7]提出,采用系统信息熵来度量学习概率的分散程度，以此估计算法进化的程度.根据信息论的观点，一个离散的随机变量X代表一个单符号离散信源，离散信源的不确定性可采用信息熵E(X)来度量.结合PBIL算法给出它的描述：设个体有N个基因位，每个基因位上有L个允许的取值，Pij代表在基因位i上取第j个值的学习概率，则用于评价PBIL算法进化程度的信息熵计算公式为

).

在进化的初始阶段，基因位上各取值的学习概率相等，此时pi=1/L，且系统熵值最大，即Emax=Eini=NlnL.随着PBIL算法进化的不断进行，各基因位的学习概率从最初的1/L分别向0或1靠近，系统的熵值E也从初始的iniE不断减小，到最终趋于0.由此可见，PBIL算法的进化过程也是系统熵值逐步下降的过程，通过系统的信息熵可以合理、准确地估计算法的进化程度.

上面讨论了算法的各组成部分,下面给出其完整程序描述:

/* BestEver is the best solution overall all the generation;numVertices is the number of nodes in graphG;Nis the number of nodes inD; */

PBIL_QoSMCR(G(V,E),s,D)

{

for (i=1;ilt;=N;i++)

Qi={p1i,…,pji,…,pki};/*use the shortest path Dijkstra algorithm to find all pathes that satisfy the QoS metric from the source node to destination nodes */

//Initizations

for (i=1;ilt;=N;i++)

for (j=1;jlt;=L;j++)

pij=1/L;

while (Egt;0)

{

for (i=1;ilt;=M;i++)

{

Individual [i]=Sample(P);

Fitness[i]=Evaluate(Individual[i]);

}

BestIndividual=FindBestIndividual(Fitness);

BestEver= (BestEvergt;BestIndividual?

BestEver:BestIndividual);

//Update the Probability Vector

piB=piB+ε(B:BestEver)

//Mutate the Probability Vector

if (Random(0,1)lt;PM)

pi=pi*(1.0-rm)+Random[0,1]*rm;

Caculate(E);//caculate the entropyE

}

}

标准Dijkstra[11]算法的时间复杂度为O(N2),这里使用改进后的前N条最短路径算法[9].文献[9]的算法复杂度为O(N3)，但是通常来说，QoS路由矩阵都很稀疏，所以采用最小优先级队列,此时时间复杂度为O(N2lgN).对于后面的遗传算法，假设进化代数为G，则时间复杂度为O(G*M).所以整个算法的关键在于前N条最短路径算法的结果是否足够优良，使得遗传算法能够在找到足够优的解的情况下快速收敛.

3仿真实验

仿真实验采用刘莹等[12]的例子，网络拓扑结构如图2 所示，节点随机编号为1到10之间的数字，节点之间的综合QoS费用在边上标出.实验时进行了简化处理，假设源节点和目的节点之间的路径都满足限制函数L(因为可以对网络拓扑结构先进行精简处理，使其都满足限制函数L，这一步骤对实验结果不会产生影响).在仿真实验中，选源节点s为节点1、目的节点集D={4,6,7,8},做随机实验.

图2 网络拓扑图

利用前N条最短路径算法[9],计算出源节点到各目的节点之间的备选路径集(L=5)，结果如表1所示.

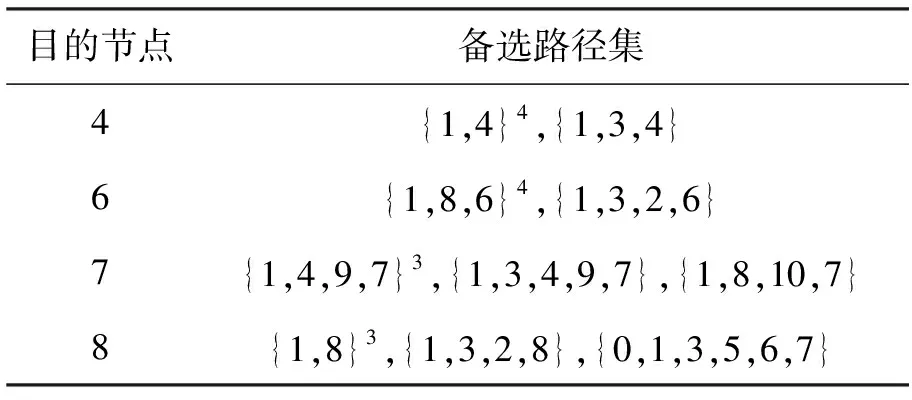
表1 源节点到每个目的节点的备选路径集

注：表中上标数字为路径出现的次数.

在仿真实验中，对PBIL算法参数，如种群规模、修正常数、终止条件、变异速率、选取多组值进行实验.结果发现：在相同条件下，种群规模越大，收敛率越高，最后趋于稳定(收敛时的代数和种群规模无关)；修正常数越小，收敛率越高，收敛时的代数也越大；变异率和变异速率的选取对算法避免早熟起决定性作用.表2、表3给出了2组不同参数下50次进化的收敛率，第1组的修正常数ε取0.01，终止条件δ≤8%Eini，变异率PM取0.01，变异速率rm取0.001;第2组的修正常数ε取0.007，终止条件和变异率、变异速率不变.分别对种群规模取2，4，8，9，10进行50次实验，记录了在满足终止条件下，不同规模的种群在50次试验中找到最优解的次数.实验1在满足终止条件下平均迭代80次，实验2平均迭代113次，但是一般都在前4代就能找到最优解，图3是满足综合参数约束的最优组播树.

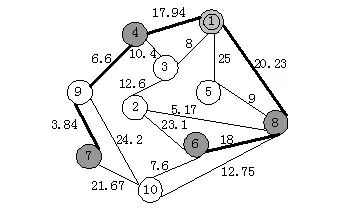
图3 满足综合参数约束的最优级组播树

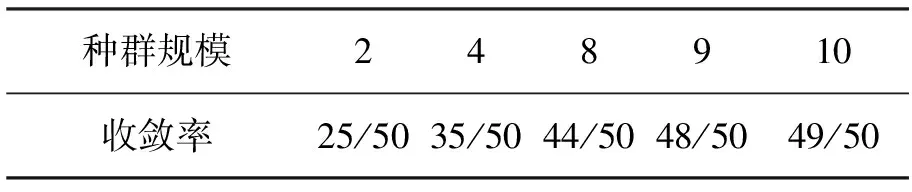
种群规模248910收敛率25/5035/5044/5048/5049/50

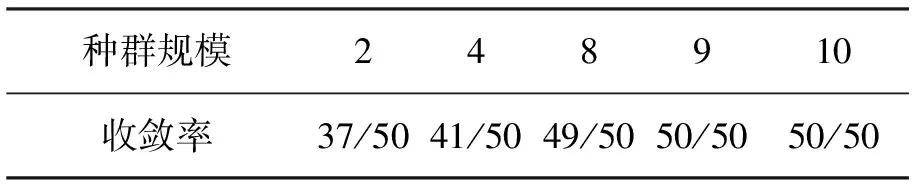
表3 ε=0.007,δ≤8%Eini下50次进化的收敛率

4 结 论

本文提出了一种基于PBIL算法的综合QoS参数的组播路由算法，该算法摒弃了传统遗传算法复杂的重组过程，避免了在重组过程中可能会破坏个体的构造块而产生连锁问题，以致算法逼近局部最优或早熟[13].引入了竞争学习的机制，以概率矩阵的方式通过采样产生下一代群体，并保留了到当前代为止的最优个体，然后选择最优个体对概率矩阵进行更新，直至最后收敛.仿真结果表明，该算法实施简单，收敛速度显著提高，并能以较大概率收敛到最优解.另外，该算法还有以下特点：基于路径的树结构编码，简化了编码操作，省略了复杂的编码解码过程.因此，该算法在网络规模较大时仍能得到很好的应用.但是，由于采用了综合QoS参数约束，特别是在网络情况比较复杂的情况下，恰当的权值变换函数很难给出.

[1]Li Layuan,Li Chunlin.A Multicast Routing Protocol with Multiple QoS Constraints[M]//Chapin L.Communication Systems:The State of the Art.Norwell:Kluwer AcademicPublisher Group,2002:181-198.

[2]包海洁，卢辉斌，栾庆林.基于遗传算法的QoS组播路由算法的改进[J].无线电通讯技术，2008，34(4)：1-3.

[3]Winter P.Steiner problem in networks:a survey[J].Networks，1987，17(2):129-167.

[4]Karp R M.Complexity of Computer Computations[M].New York:Plenum Press，1972:85-103.

[5]Baluja S.Population-Based Incremental Learning:A Method for Integrating Genetic Search Based Function Optimization and Competitive Learning[R].Pittsburgh:Carnegie Mellon University,1994.

[6]Hoehfeld M，Rudolph G.Towards a Theory of Population-Based Incremental Learning[C]//Proceedings of the 4th IEEE Conference on Evolutionary Computation.Piscataway NJ:IEEE Press,1997:1-5.

[7]李二森，郭海涛，张保明，等.PBIL算法在遥感影像匹配中的应用[J].武汉大学学报:信息科学版，2008，33(2)：140-143.

[8]邹阳，宁卓，许道云,等.面向QoS的路由数学模型及求解[J].贵州大学学报:自然科学版，2000，17(4)：258-263.

[9]柴登峰，张登荣.前N条最短路径问题的算法及应用[J].浙江大学学报:工学版，2002，36(5)：531-534.

[10]周明，孙树栋.遗传算法及应用[M].北京：国防工业出版社，1999.

[11]Thomas H C,Charles E L,Ronald L R.Introduction to Algorithms[M].Cambridge;MA:MIT Press,1990.

[12]刘莹，刘三阳.多媒体通信中带度约束的多播路由算法[J].计算机学报，2001，24(4)：367-372.

[13]Harik G R,Goldberg D E.Learning Linkage[M]//Belew R K,Vose M D.Foundations of Genetic Algorithms.San Francisco:Morgan Kaufmann Publishers Inc,1997:247-262.

(责任编辑 陶立方)

TheQoSmulticastroutingalgorithmbasedonPBIL

CHEN Jianming

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

A new QoS multicast routing optimization algorithm was proposed based on PBIL algorithm which would help to find a low-cost multicast routing tree with integrated QoS parameter constraint. The PBIL algorithm combined genetic algorithm and competitive learning effectively and would be efficient in large scale networks by tree structure coding scheme based on path and prepared path set based on probability. Verified simulation showed this algorithm with efficiency and effectiveness.

Steiner tree; Quality of Service; group broadcast; genetic algorithm; Population-Based Incremental Learning algorithm

1001-5051(2010)01-0070-05

2009-11-09

浙江省科技厅科研项目(2009C31118)

陈建明(1957-)，男，浙江诸暨人，副教授.研究方向：信息安全.

TP391

A