压电陶瓷的非线性特性校正研究

缪 建,朱若谷,郭 斌,黄 宇

(中国计量学院计量测试工程学院,浙江杭州310018)

虽然基于多光束干涉原理的F-P干涉术已经有一百多年的历史[1,2],但是把它作为长度计量中的标准器具到构成激光器的谐振腔来研究还是比较新颖的,不管是理论研究还是实验研究都是经久不衰的研究热点.目前,除了可以用它作为高分辨率光谱仪的色散元件以外,还可以用于激光稳频、光波长、腔内介质参数、微小位移等物谐振腔结构.

结合在研究光纤F-P微小位移测量中遇到的情况,对压电陶瓷扫描调相F-P干涉仪作非线性影响的讨论,显然,给出的结果可应用于相关几何量测量传感器的误正.

1 原 理

一般情况下可以用一个二次项表示压电陶瓷的非线性电致伸缩,即位移量:

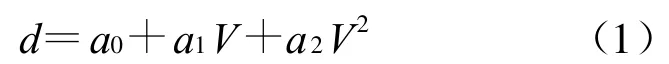
下面分别对应三种调制电压,即:阶跃电压、锯齿波电压和正弦波电压,讨论压电陶瓷的非线性对相调F-P干涉术的影响.

1.1 阶跃电压调制

为分析简便起见,作相应近似,即在光强极大值附近作信号调制,而且精细系数F与位相Φ满足F·Sin2φ远小于1以及阶跃电压通过N步从0升到V0,那么投射光强可以表示为[3,4]:

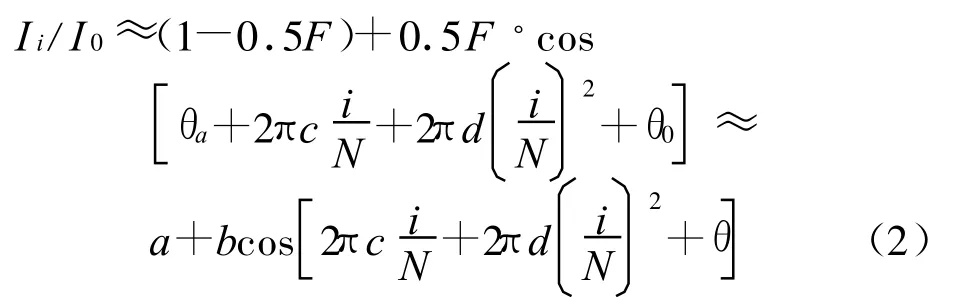
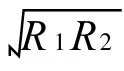
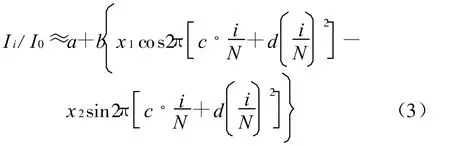
其中:i=0,1,2,…,N,进一步对式(3)分块求和,设分块数为M,则有:

并作简化处理,设ti=i/N,则有:

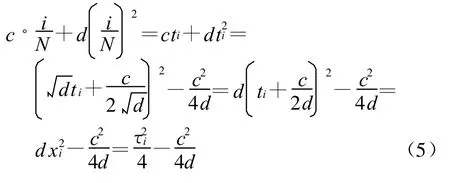
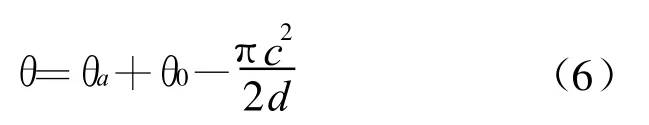
则式(4)可以化为:

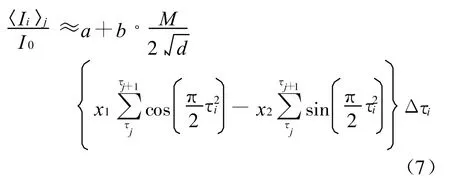
1.2 锯齿波电压调制

这时的调制电压可表示为:

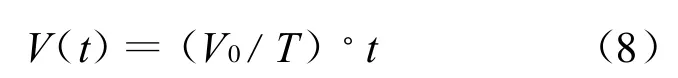
取与阶跃电压调制相同的近似条件,这时仅需要把式(7)中的求和形式改成求积分形式就可以了 ,即

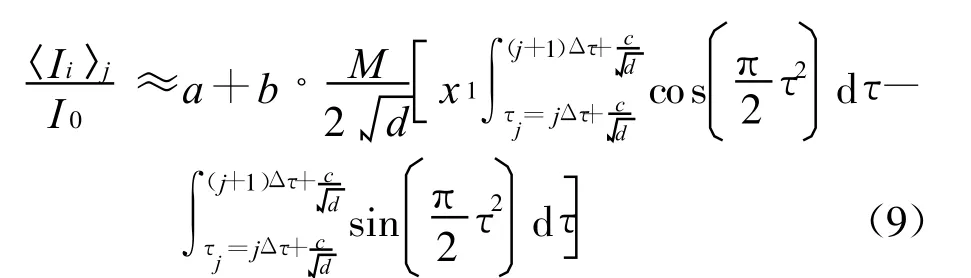
1.3 正弦波电压调制

这时调制电压表示为

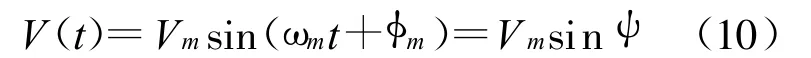
式(10)中:Vm—正弦波调制电压的幅值;ωm和φm—角频率和初相位.同时为了简便起见设ψ等于ωmt加上φm[7,8].

压电陶瓷的电致伸缩特性表示为

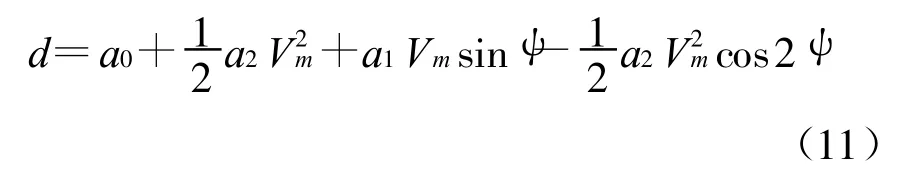
作与前相同的归化处理.则透射光强公式中的位相角 Φ可表示为

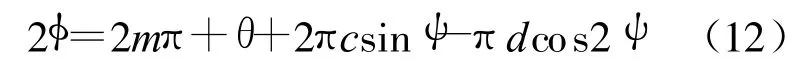
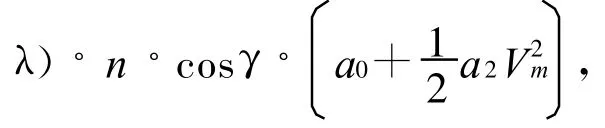
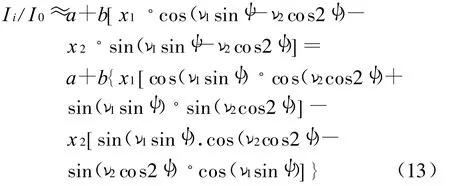
式(13)中 :ν1=2πc,ν2=πd.

设 cos(δ φt)=cos(ν1sinψ-ν2cos2ψ),则当 n为偶数时 ,cos(δ φt)为下式,取正号.

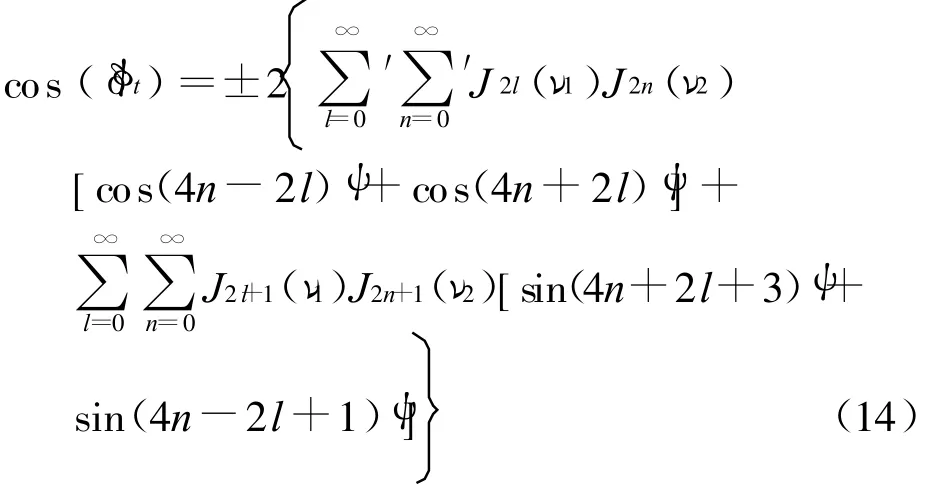
当n为奇数时,式(14)取负号,∑′表示首项系数为1.

设 sin(δ φt)为 sin(ν1sinψ-ν2cos2ψ),则 sin(δ φt)可表示为:

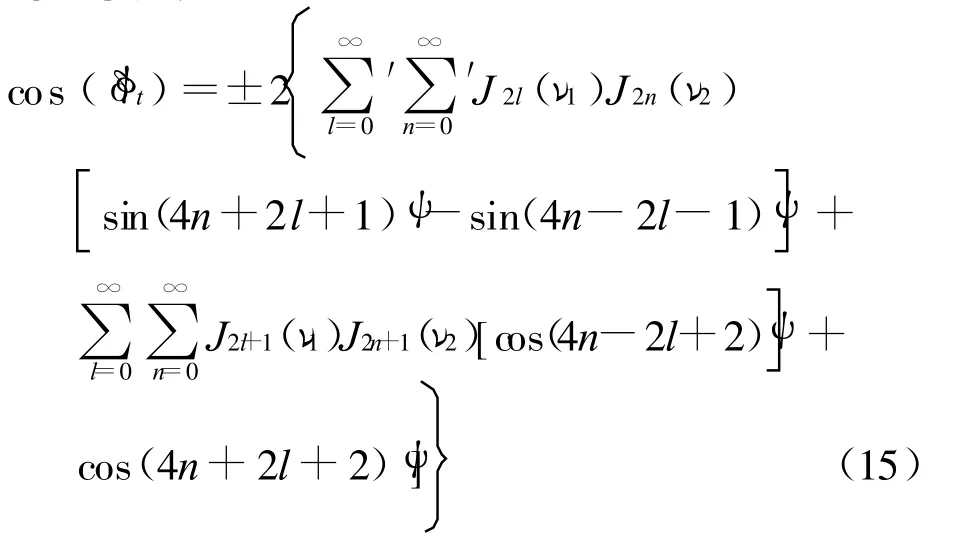
同样当n为偶数时,选取正号,n为奇数时,选取负号.由式(14)与式(15)可以估算出主要低次谐波和零频率成分的表示,其中略去高于5阶贝赛尔函数因子项.

1)零频率成分

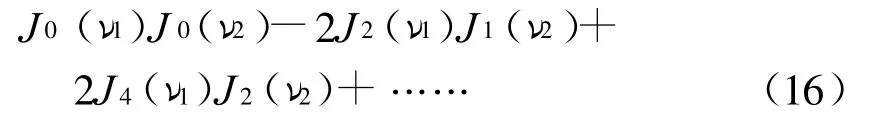
2)一次谐波成份幅值

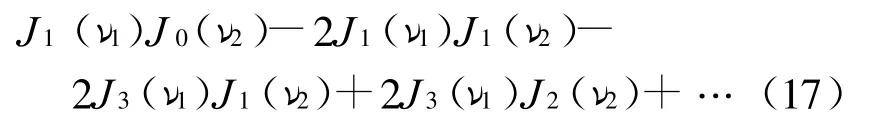
3)二次谐波成份幅值

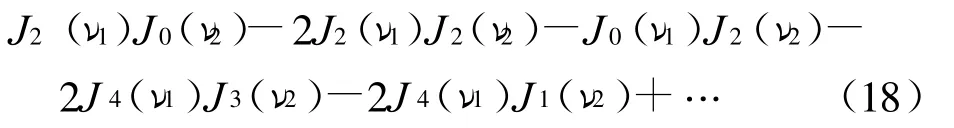
上述方法比较繁琐,下面介绍一种比较简洁的方法.重写透射光强表达式(13)为:

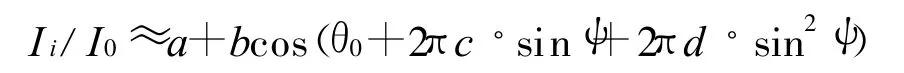
作变量替换,设:

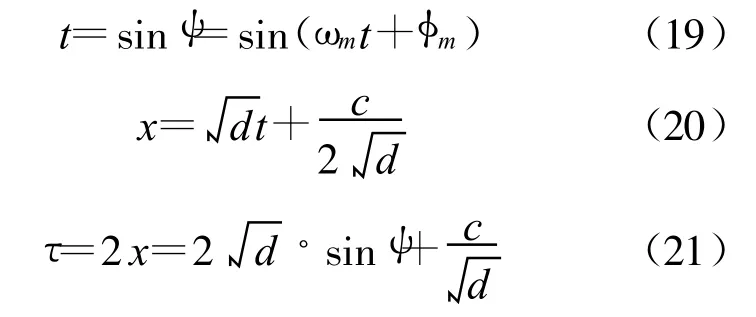
则上述的投射光强公式可化为:

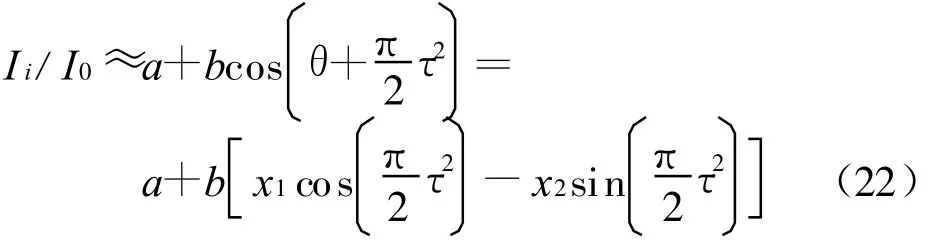
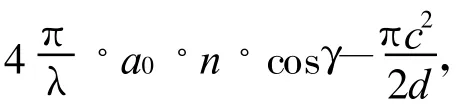
这时的分段积分光强〈Ii〉j可表示为:

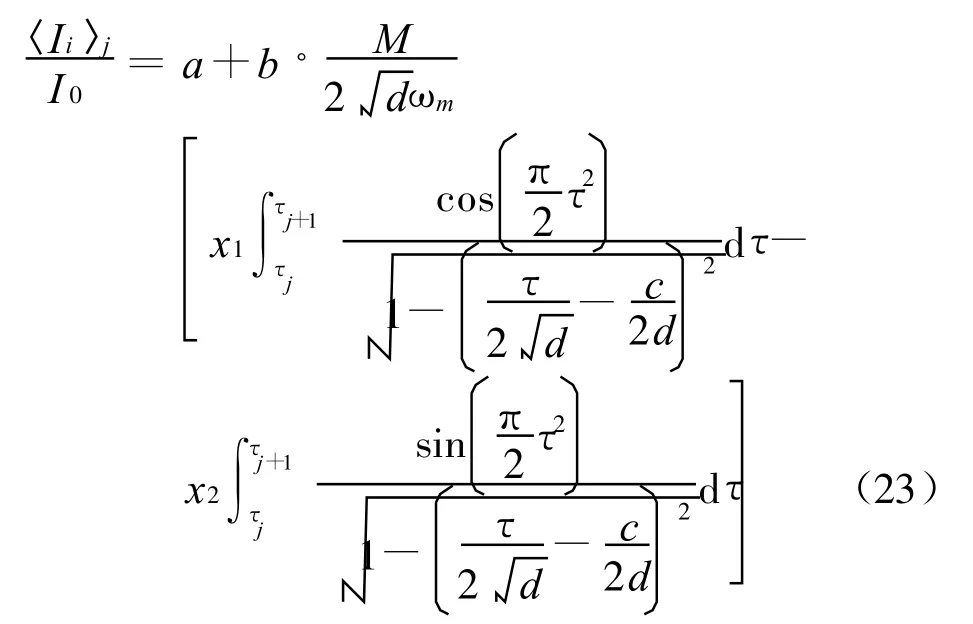
当上式应用数值积分求解时,设时间从0变到T,把积分时间T细分N段,在N段中又均分M块,各块的积分上下限可由下式表示:

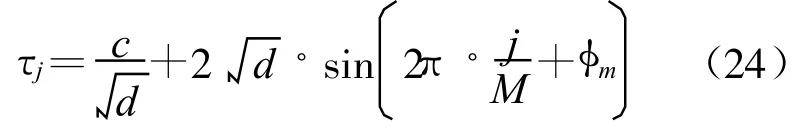
式(24)中 :j=0,1,2,…,M.

最后得出,为了检验或修正非线性影响,对应阶跃或锯齿波扫描,可以根据以下公式(25)和(26)计算初位相.

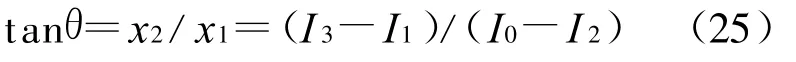
对应正弦调制,其初位相计算式为:

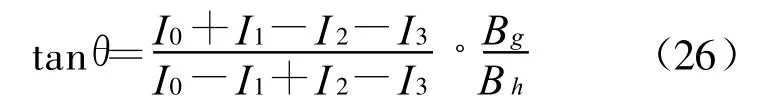
其中 x=4πa/λ,a为调制电压产生的振幅.

2 实验及结果

首先通过实验室测定常用的PZT压电陶瓷非线性系数,然后利用上面给出的结果进行数值计算.下面简单地介绍测定压电陶瓷非线性系数的方法.一般有两种方法,即方法一:扫描调相干涉法.在通常的迈克尔逊干涉仪参考镜后粘结压电陶瓷,然后调节加在压电陶瓷上的偏置电压,可以测出干涉光强与电压V的关系,用I(V)表示,进一步由迈克尔逊干涉仪的输出光强公式

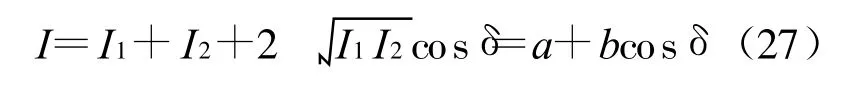
式(27)中:a为光强的直流成分I1+I2,b为光强中的交流成分的幅值2 I1I2.I1与I2分别为两臂光强.通过阶跃电压扫描给出最大光强Imax与最小光强Imin,就可以得出a与b:

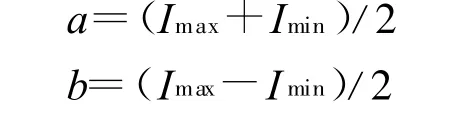
从而由下式给出位相变化δi和位移变化di,即:

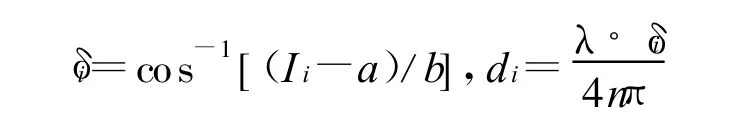
式中:i等于1,2,3,…N为阶跃电压步进数,λ为光波长,n为介质折射率.

最后由N对数组(di,vi)用曲线拟合或二元回归算法可以得到位移电压之间的拟合公式:

方法二为直接测量法.虽然这种方法简单,但是精度不高.它受电感测微仪的分辨率限制,其位移变化估读到0.01 μ m,用电感测微仪(或其它测微装置)直接测量给出(di,vi)数组.最后用相同的数据处理方法得出式(32),故称直接测量法.

对无锡国营第七二一厂生产的压电陶瓷(PZT-5)的实测结果为:

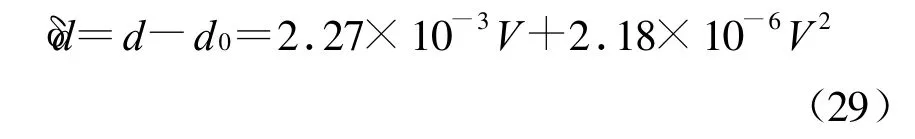
式(29)中:d的单位为μ m,V的单位为V.

经归化处理后C为0.99,d为0.133,两者均为无量纲数.

为节省篇幅,表1和表2分别给出初相位为零和π/4附近的理论给定值和分块积分光强计算值(对应于采用阶跃电压扫描法).

表1 零位相比较Table 1 Comparison of zero phase

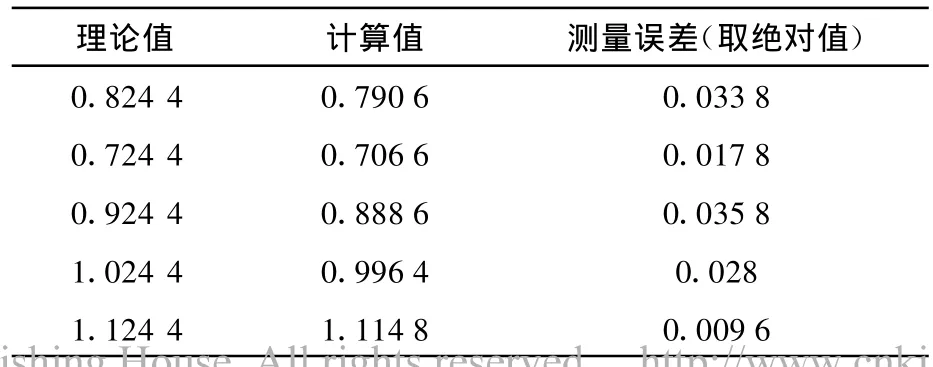
表2 π/4位相附件比较Table 1 Comparison of π/4 phase

由上述表列数据明显地表示在π/4处位相测量误差小于零值附近,通过类似比较也可以发现在π/2位相附件误差也明显地大于 π/4位相邻域.

计算程序中使用的位相计算公式为(26).

3 结 语

对压电陶瓷的非线性影响作了理论分析,把Chiayu Ai等人的结果推广到正弦相调干涉术,并实际测量了压电陶瓷的非线性系数,介绍了两种测量方法并在实测数据基础上进行数值计算,最后给出的结论为除了Chiayu Ai等人提出的分前后两组相互移相90°(对应四块积分法)测量抵消误差以外,在小调制信号时还应注意工作点在π/4初位相附近,并避开零值与±π/2位相邻域.特别在非线性系数 d较大的时候更应该如此,至于如何正确校正的讨论由于受到篇幅所限将另文讨论.

[1]朱若谷.激光应用技术[M].北京:国防工业出版社,2006:140-151.

[2]AI C,WYANT J.Effect of piezoelectric transducer nonlinearity on phase shift interferometry[J].Applied Optics,1987,26(6):1112-1116.

[3]朱若谷.一种新的简易调相干涉术[J].计量技术,1989(6):1-2.

[4]朱若谷,陈永本.双法布里—珀罗干涉仪的非线性控制[J].计量学报,2000,21(4):253-259.

[5]ZHU R G.Nonlinear control of double Fabry-Perot interferometer[J].SPIE Proceeding Series,1996,24(8):319-324.

[6]周 云,蒋魁强,王珊珊.铌酸钠钾基压电陶瓷的结构与性能研究[J].中国计量学院学报,2009,20(1):30-34.

[7]王向朝.激光干涉仪与纳米精度检测[J].中国计量学院学报,2001,12(2):43-48.

[8]孙流星,于瀛洁.基于波长移相的改进加权多步算法[J].中国计量学院学报,2004,15(4):61-67.

[9]王希花,郭书祥,汝长海.基于压电陶瓷迟滞非线性的建模方法[J].哈尔滨工程大学学报,2010,31(1):271-276.

[10]崔王国,孙宝元,董维杰.压电陶瓷执行器迟滞与非线性成因分析[J].光学精密工程,2003,11(3):271-276.