漂珠/微硅复合水泥浆体系的抗压强度与密度和温度之间的相关性研究
李东山 (大庆钻探工程公司钻井生产技术服务二公司)
苏海光 (大庆钻探工程公司钻井生产技术服务一公司)
刘忠华 (成都理工大学能源学院)
漂珠/微硅复合水泥浆体系的抗压强度与密度和温度之间的相关性研究
李东山 (大庆钻探工程公司钻井生产技术服务二公司)
苏海光 (大庆钻探工程公司钻井生产技术服务一公司)
刘忠华 (成都理工大学能源学院)
固井水泥浆抗压强度是固井质量的重要参数,而地层温度和水泥浆密度是影响抗压强度的重要参数指标。本文结合近年来苏丹1-2-4区块漂珠/微硅复合水泥浆体系的广泛应用与国内学者对该水泥浆体系进行的室内理论研究,利用多元回归分析方法对实验所得该水泥浆体系的抗压强度等重要参数进行线性回归分析,得到线性回归模型。结果表明,漂珠/微硅复合水泥浆体系的抗压强度与实验温度 (模拟地层温度)、水泥浆密度之间确实存在着线性相关关系,应用回归模型可以计算其抗压强度,从而对固井现场施工起到指导作用。
漂珠/微硅复合水泥浆体系抗压强度 密度 温度 线性回归
针对近年来苏丹1-2-4区块固井施工过程中所遇地层的压力系数低、破裂压力小等特点,为了保护产层,防止水泥浆的高失水污染油气层,水泥浆必须低失水。低密度高强度水泥浆体系已经广泛应用于固井施工现场,同时国内许多学者对低密度高强度水泥浆体系也进行了系统的室内理论研究。通过对地层资料、井身结构、固井工艺等环节的分析、研究,经过大量的室内试验和现场应用,得到性能优良的低密度高强度水泥浆体系,解决了该地区固井技术难题,从而满足苏丹1-2-4区块进行的固井施工[1]。
漂珠是火电厂烟筒中的尘灰,通过水中收集漂在水面的煤灰,烘干后作为减轻剂加入水中配制低密度水泥浆,可使水泥浆密度降低到1.4 g/cm3或更小。由于漂珠壁面对水具有渗透作用,因而多用于中低温井或低压井固井。漂珠低密度水泥在长庆、中原、大庆、青海、胜利、四川、克拉玛依、吐哈等油田都有广泛的应用。
微硅也称超细硅粉,是铁合金生产过程中分离出来的一种副产品,可以从多种途径获得,如球磨石英砂、火力发电厂烟道粉尘、硅铁合金生产过程中得到的副产物硅灰等。其主要成分是SiO2(含量在90%~98%),硅灰的密度约为2.6 g/cm3,粒度很小,平均粒径为0.1μm,比水泥平均粒径(70μm)和漂珠平均粒径 (150~250μm)小得多,粒度分布范围为0.02~0.5μm。由于粒度小,比表面积大,氮吸附 (BET)测定值为15~20 m2/g,是油井水泥的50~60倍[5]。
漂珠/微硅复合水泥浆体系的配制:根据Furnas颗粒堆积最密实级配原理,配制低温、早期抗压强度高、低密度水泥浆。即在第一级大颗粒堆积空隙中充填进比第一级大颗粒小得多的第二级粒子,第二级粒子充填满第一级颗粒空隙后,总体积不变;然后用粒径比第二级粒子小得多的第三级粒子充填满第二级颗粒空隙,总体积仍保持不变;依次继续填入更小的粒子,使总体积不变,从而获得堆积空隙率最小的混合体[6]。
漂珠/微硅复合水泥浆体系的性能特点:水泥石的早期抗压强度高;水泥浆失水控制好,有利于保护油气层,防止损害;水泥浆凝结过程中的稳定性好,无析水,浆体不分层,凝结后水泥石的纵向密度分布均匀;水泥浆固相颗粒堆积密实空隙率低,凝结水泥石致密,孔隙连通性差,防气窜效果好[7]。
针对漂珠/微硅复合水泥浆体系,进行了广泛的现场应用和理论研究,但是在固井施工现场能否利用该水泥浆体系的一些指标参数来衡量抗压强度指标,并未得到解决。本文利用多元回归分析理论对一些国内外使用过的低密度高强度水泥浆体系的抗压强度与密度及温度的实验数据进行了线性回归分析,从而得到了漂珠/微硅复合水泥浆体系的抗压强度与密度及温度之间的回归模型,该回归模型可以指导水泥浆体系的现场固井施工。
1 水泥浆体系的抗压强度与密度和温度之间的回归分析
1.1 抗压强度关于密度的散点图
由散点图 (图1~图4)可以看出,无论实验温度是否相同测量的水泥浆体系的抗压强度与密度之间都似乎存在着某种线性相关关系,据此对这两个参数进行线性回归分析。
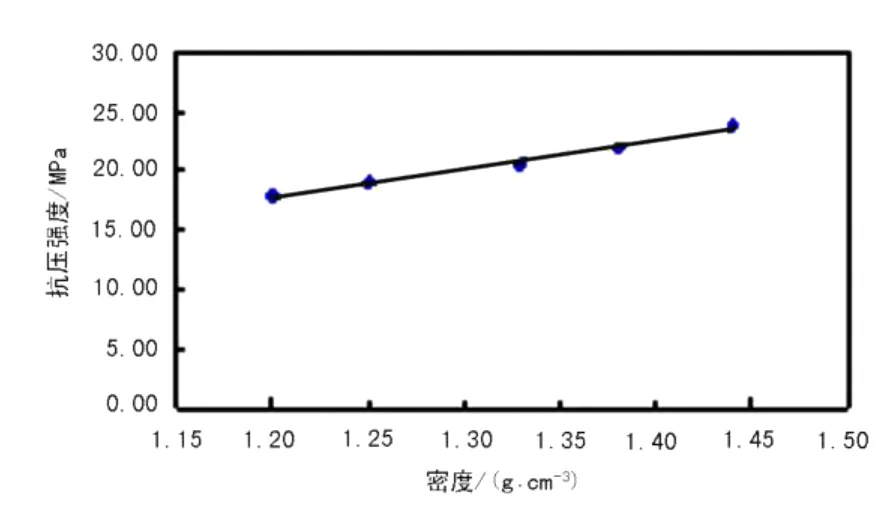
图1 170℃时抗压强度关于密度的散点图
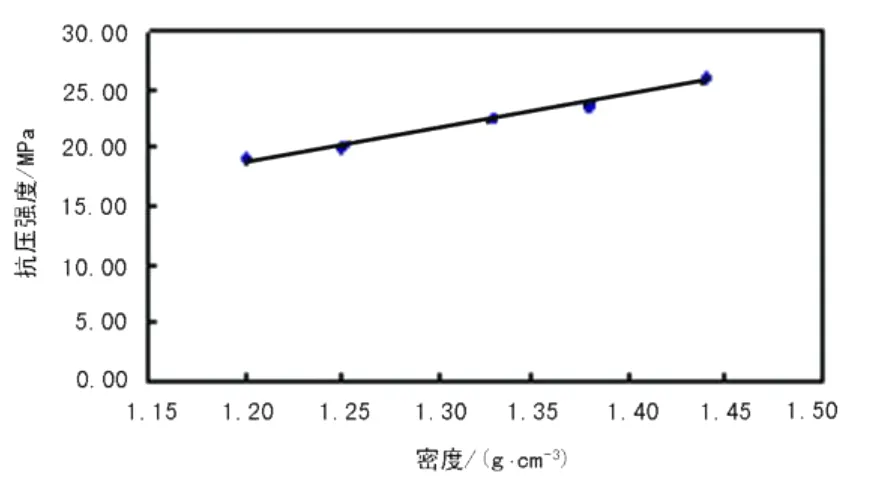
图2 90℃时抗压强度关于密度的散点图
1.2 抗压强度关于密度的回归方程
对在70℃条件下测量的不同配方的水泥浆体系的抗压强度和密度数据 (表1,序号1~5)进行相关性分析,得到回归方程:
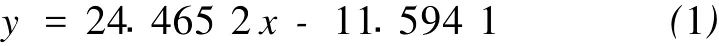
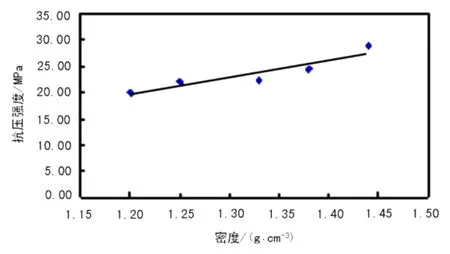
图3 110℃时抗压强度关于密度的散点图
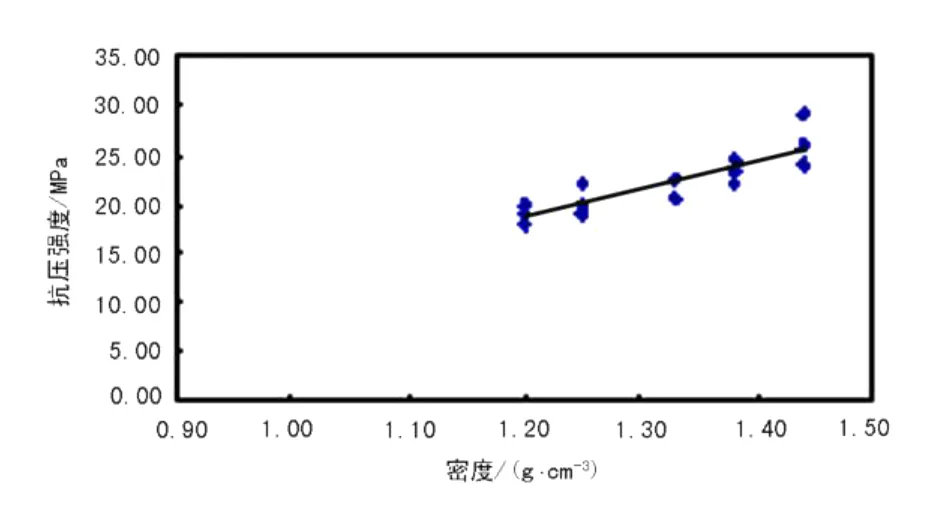
图4 不同温度时抗压强度关于密度的散点图
对在90℃条件下测量的不同配方的水泥浆体系的抗压强度和密度数据 (序号6~10)进行相关性分析,得到回归方程:
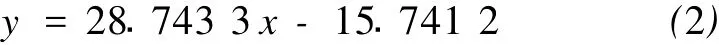
对在110℃条件下测量的不同配方的水泥浆体系的抗压强度和密度数据 (序号11~15)进行相关性分析,得到回归方程:
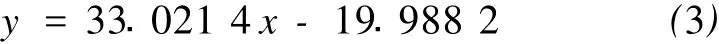
对在不同温度条件下测量的不同配方的水泥浆体系的抗压强度和密度、温度之间的数据 (序号1~15)进行相关性分析,得到回归方程:

表1 水泥浆体系的实验数据
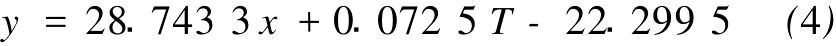
1.3 回归方程的显著性检验
在回归分析中用复相关系数 R作为判断回归方程的回归效果是否显著的参数。判断标准是:R越接近1,回归效果越好。
利用计算公式[4]得到:
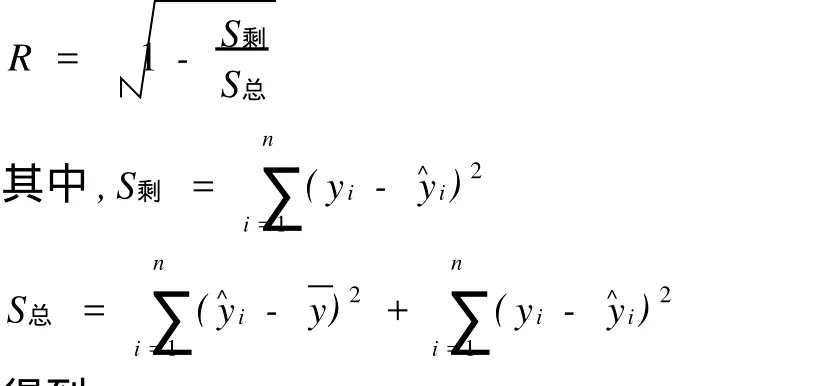
◇70℃条件下回归方程的复相关系数 R=0.990 9;
◇90℃条件下回归方程的复相关系数 R=0.993 6;
◇110℃条件下回归方程的复相关系数 R=0.934 5;
◇不同温度条件下回归方程的复相关系数 R=0.966 1。
故可以判断各试验温度下回归方程的回归效果都好。
1.4 线性回归方程的预测精度估计
由统计学区间估计理论可知,在随机变量y服从正态分布情况下,任一给定的自变量值 (x1,x2,…xm),所对应因变量 y的真值y以95%的概率落在区间是 (x1,x2,…xm)的回归值,即预测值与真值y之差有95%的概率使得所以 r剩越小其预测值精度就越高[4]。
利用剩余标准差公式[4]
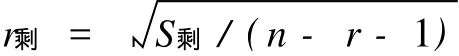
可以得到:
◇70℃条件下回归方程的剩余标准差为0.371 6;
◇90℃条件下回归方程的剩余标准差为0.365 6;
◇110℃条件下回归方程的剩余标准差为1.404 6;
◇不同温度条件下回归方程的剩余标准差为0.822 1。
故可以判断,回归方程的预测精度是比较精确的。
2 认识与结论
各回归模型相关系数均在0.93以上,且有较小的剩余标准差。说明各回归模型可以在实际工作中使用,且均有很高的计算精度。
通过计算得到的各回归模型,不仅定性地说明了在该地区漂珠/微硅复合水泥浆体系的抗压强度与密度、温度之间确实有正相关性,而且建立了三者之间的回归模型,从而对漂珠/微硅复合水泥浆体系的现场固井施工起到了良好的指导作用。
通过数学模型的使用可以减少对该水泥浆体系进行试验的次数,进一步减少成本支出。
建议在苏丹1-2-4区块推广应用漂珠/微硅复合水泥浆体系,为该区块固井质量的提高做出贡献。
[1]高兴原,李喜峰,李国金,等.低密度高强度水泥浆体系在苏丹1/2/4区块的应用[J].天然气工业,2005,25(12):58-61.
[2]孙新华,冷雪,郭亚茹,等.高强低密度水泥浆体系的研究[J].钻井液与完井液,2009,26(1):44-46.
[3]刘崇建,黄柏宗,徐同台.油气井注水泥理论与应用[M].北京:石油工业出版社,2001.
[4]郭科,龚灏主编.多元统计方法及其应用[M].电子科技大学出版社.2003.
[5]李基福.复合型低密度水泥浆调整井固井中的应用[J].石油钻采技术(固井技术),1998(6).
[6]刘德平.微硅低密度水泥固井技术研究[J].天然气工业,2001.
[7]张国华.微硅低密度水泥浆的应用[J].石油钻采工艺,1993.
10.3969/j.issn.1002-641X.2010.12.012
2010-05-13)

