基于Delaunay三角网的等高线骨架提取算法

鲁 刚,王福全

(嘉兴市规划设计研究院有限公司,浙江 嘉兴 314050)

基于Delaunay三角网的等高线骨架提取算法

鲁 刚,王福全

(嘉兴市规划设计研究院有限公司,浙江 嘉兴 314050)

根据等高线数据直接建立不规则三角形网络模型往往会在山顶、山底、山脊和山谷等特殊地区出现“平三角形”,导致模型失真。文中基于Delaunay三角网,通过对“平三角形”的处理,提取骨架线,并结合地形特征估计其高程值。实验证明该算法能够有效地提取各种地形骨架线,对于建立逼真的数字地面模型和进行数字地形分析具有重要应用价值。

Delaunay三角网;平三角形;骨架线;等高线

地形骨架线信息对于地形表面的逼真模拟和数字地形分析如地貌单元划分和水文分析等具有十分重要的价值[1-2]。传统地面测量和摄影测量中的选择性采样都通过采集骨架线信息来确保地形模拟的质量和提高工作效率。而一般等高线和 Grid形式的数字高程模型(DEM)往往不再记录这些特征信息[3-4]。如果没有骨架信息约束,根据等高线数据直接建立不规则三角形网络模型往往会在山顶、山底、山脊和山谷等特殊地区出现“平三角形”,导致模型失真。

消除这种“平三角形”导致的模型失真,一种最有效的方法就是增加辅助信息[5-6]。而从等高线数据中自动提取出骨架线和特征点等则是主要的途径[5-6]。随着大量已有等高线数据的广泛应用,从等高线中提取骨架线的研究日益重要。

1 基于Delaunay三角网的等高线骨架提取算法

Delaunay三角形广泛用于地图综合、邻近关系处理、分布范围搜寻等[7]。将等高线作为约束线段建立Delaunay三角网是从等高线生成 TIN模型的常用方法[1]。为了消除平三角形,首先根据等高线生成的Delaunay三角网,从平三角形出发,利用三角形的相邻关系,跟踪出弯曲部分骨架所要经过的三角形,取其经过边的中点作为骨架点,最后将这些点连接骨架线,进而估算获得这些骨架点的高程值,最后再补充到原始数据中重新建立约束Delaunay TIN。基于Delaunay三角网提取骨架线的算法流程如图1所示:①等高线数据生成约束Delaunay三角网;②三角形初始化,提取叶骨架;③提取中间骨架、鞍部骨架和环形骨架,确定主骨架;④骨架线高程估计。

图1 基于Delaunay三角网提取骨架线的算法流程

1.1 数据预处理

目前,大量的等高线数据是由现存的地形图数字化及后处理得到,在对栅格数据进行矢量扫描的过程中难免出现一些错误[7-8],为了下一步确定三角形类型的需要,保障算法的稳定,必须对等高线数据进行预处理,将等高线上除起始点外的重复数据剔除。然后将等高线作为约束线段建立Delaunay三角网。

1.2 三角形初始化

首先在初始三角网中根据平三角形三个顶点高程值相同的特点搜索平三角形,并根据三角形的连通性即骨架线穿越的三角形边的条数确定三角形的类型。三角形连通性判断标准如下:①骨架线不可能与等高线相交,所以三角形的边若位于等高线上,则该边不可能有骨架线通过。②三角形某条边邻接的三角形为平三角形,在满足标准①的条件下,该边必定有骨架线通过。

由此将初始三角网内的三角形分为四类:第一类:一条边有骨架线通过的三角形,这类三角形为骨架线的起始或终止三角形。其中的平三角形,被称为叶子三角形,是叶骨架的起始三角形;而非平三角形可能是鞍部骨架的起始三角形或者骨架的终止三角形。第二类:两条边有骨架线通过的三角形。第三类:三条边都有骨架线通过的三角形,即分支三角形,骨架线汇合与此类三角形。最常出现的情况是两段骨架线在该类三角形汇合,然后骨架线从第三条边相邻的三角形延伸;在山顶或山谷最内圈等高线区域内,分支三角形是骨架线的终止三角形,即有三条不同方向的骨架线终止于该三角形的三边。第四类:其他的三角形没有骨架线通过,这类三角形所在区域地形表面模拟较为准确,因此本文不考虑这类三角形所在区域的骨架提取。

1.3 骨架线提取

本文算法的基本思想是沿起始三角形非等高线边遍历平三角形,直到非平三角形或者分支三角形为止。在骨架线中顺序记录经过的每一个三角形,将两三角形公共边的中点作为骨架点,完成一条骨架线的三角形遍历。在这个过程中,除了遍历三角形提取骨架点之外,还应记录与其邻接的骨架线。具体流程如下:

1)处理平三角形,计算当前三角形骨架前进方向所在边对应角的大小,若角度超过一定阈值如120°,则该三角形不再作为骨架三角形;若角度在阈值范围内,记录骨架线起始点,进入其邻接的三角形:如果当前三角形是第一类三角形,表示一条骨架线已经遍历完成,记录骨架线终止点。对于短小骨架,比如其遍历三角形只有两个,且无前续、后续骨架线,则剔除该条骨架线;如果当前三角形是第二类三角形,继续行进的方向就是唯一的,记录骨架点,进入相应的邻接三角形;如果当前三角形是第三类三角形,则继续前进的方向就有两种可能,这时一条叶骨架遍历完成。

2)处理分支三角形集中已处理两次的三角形。确定两条分支中的主骨架线后,以当前分支三角形为起始三角形。

3)提取鞍部骨架,其起始三角形为第一类三角形中还未处理的非平三角形。

4)最后提取环形骨架,其起始三角形为分支三角形集中只处理过一次的三角形。

经过上述处理,普通平地形骨架线、鞍部骨架线及与外部连通环形骨架线都能得到正确处理,因为在处理分支三角形生成中间骨架线的过程中,新的骨架可能还会在另外的分支三角形处停止,因此,这里总是处理分支三角形集中第一个满足条件的三角形,循环中间骨架跟踪过程,直到满足条件的三角形数目为0。

1.4 主骨架线确定

骨架提取过程中需要确定主骨架线,得到骨架线之间的邻接关系。主骨架线主要针对线性结构延展十分明显的区域,反映的是骨架线的形态特征和主延伸方向。从分支三角形开始遍历中间骨架时,如果两条分支骨架的后续骨架都为当前遍历的骨架,但当前遍历骨架的前续骨架只记录为两条分支骨架中的一个。于是,这里的问题就是如何确定两条分支骨架中哪条作为前续骨架的取舍标准。

本文结合这两方面考虑,但主骨架的确定属于空间认知的内容,是一个不确定性问题,选取的标准并不是唯一的,要根据具体的情况来调整。同时,有一些分支骨架长度、宽度都相当,这时选择其中任何一个都可。根据骨架线顺序经过的三角形,依次将骨架点相连,即可得到骨架线。

2 骨架线高程估计算法

要将上述骨架线插入三角网消除平三角形,每个点都应具有正确的高程信息。需要利用骨架线与等高线之间的相互关系来估计高程值。对于两条等高线之间骨架线高程估计的基本思想是:根据骨架线上起始点及终止点的高程值,线性内插所遍历的骨架线上的所有点的高程。对于骨架线存在于等高线内部,没有其他参考点时,例如山顶,往往假设山顶中间一点为最高点,但实际情况中,山顶不一定是中间取极值,有可能偏于某一边,也有可能存在多处极值。所以,山顶的插值过程最好能由山顶本身的形状、骨架几何特性、周围局部地形来处理。

2.1 基本骨架线插值

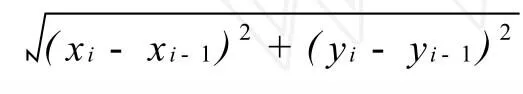
内插出主骨架上各点的高程值后,按同样的方法内插出该主骨架所有分支骨架上各个骨架点的高程,只是骨架线的起始点或终止点为内插得到的点,而非原等高线上存在的离散点。

2.2 局部地形插值

对于山顶、山谷及鞍部区域,骨架线起始点和终止点高程值会出现相等的情况,即|Zl-Zf|=0,且等高线内部没有其他参照点。本文算法考虑局部地形变化,利用骨架产生的几何性质,将这类区域的骨架线高程估计分为如下两步:

首先,由于地形表面的连续性及山顶性质相似性,局部小区域内可认为地形表面一侧几近于线性变化,因此相邻近的两点处地形表面的斜率相近(或者带有小许偏差α,α可由实际地形状况决定)。然后,根据上述方法得到山顶或鞍部区域插值结果,判断出该区域的最高点,以此点为基础,沿骨架线对其他骨架点进行拟合。上述两步既考虑到高程估计的合理性,又考虑到地形的连续性,使地形模拟更接近真实情况。

对于环形区域,如果环形区域与外界连通,根据外界骨架点的高程,内插环形骨架点高程;如果环形区域封闭,则根据环形区域外临近的等高线变化趋势,估计环形骨架点的高程值。

3 实验分析

为了验证上述算法的正确性和有效性,选择山地类等高线图进行了实验,结果分别如图2所示。可见,由于骨架线信息的正确提取和高程估算,最终的 TIN模型都逼真地表达了实际地形特征。

图2 山地区域等高线、骨架线、TIN透视图

4 结束语

将具有高程值的骨架线插入三角网中可以消除原Delaunay三角网中存在的平三角形,改善地形模拟的准确性。而一些明显不合理的骨架线通常是由等高线的断裂或赋值错误造成的,因此,通过对等高线骨架的处理还可以辅助监测等高线数据中存在的错误。

[1]李志林,朱庆.数字高程模型[M],2版.武汉:武汉大学出版社,2003.

[2]GÜLGEN F.,GÖKGÖZ T..Automatic extraction of terrain skeleton lines from digital elevationmodels[J].International A rchieves of Photogrammetry Remote Sensing and Spatial Info rmation Sciences,2004,35(3):372-377.

[3]刘泽慧,黄培之.DEM数据辅助的山脊线和山谷线提取方法的研究[J].测绘科学,2003,28(4):33-36.

[4]陈仁喜,龙毅.顾及三角形处理的 TIN建立算法[J].武汉大学学报:信息科学版,2003,28(5):619-622.

[5]眭海刚,朱庆.一种从DLG生成高质量DEM的混合方式[J].测绘通报,2001(4):16-18.

[6]黄培之.提取山脊线和山谷线的一种新方法[J].武汉大学学报:信息科学版,2001,26(3):247-252.

[7]GOLD C.M.,SNOEYINK J..A one-step crust and skeleton extraction algo rithm[J].Algorithmica,2001,30:144-163.

[8]艾廷华,祝国瑞,张根寿.基于Delaunay三角网模型的等高线地形特征提取及谷地树结构化组织[J].遥感学报,2003,7(4):292-299.

Skeleton extraction algorithm based on the Delaunay triangulation of contour lines

LU Gang,WANG Fu-quan
(Jiaxing Planning&Resarch Institute Co.,L td.,Jiaxing 314050,China)

By means of the contour lines to construct the triangulated irregular netwo rk(TIN)model,the“flat triangles”are usually generated at the significant topographical areas such as hilltop,ridge,o r valley,w hich results in the distortion of the digital terrainmodeling.In thispaper,aiming at the p rocessing of“flat triangles”,the algorithm for skeleton extraction and elevation evaluation from the contour lines based on the Delaunay triangulation is introduced.Experimental resultsp rove that various skeletons can be correctly extracted,w hich are useful to the realistic digital terrain modeling and corresponding digital terrain analysis.

Delaunay triangulation;flat triangle;skeleton;contour lines

P23;P208

A

1006-7949(2010)06-0013-04

2009-09-28

鲁 刚(1978-),男,工程师.

[责任编辑张德福]