分形特征的模拟电路故障诊断方法

李 伟，李天伟，王桂军，易成涛

（海军大连舰艇学院航海系，辽宁 大连 116018）

1 引 言

据统计，在电子系统中模拟电路的故障占到总故障的80%。模拟电路故障诊断成功与否关键集中在信号测量、信号处理、信号特征提取及分析诊断几个环节，由于元器件容差、功能和结构的复杂性、非线性及不确定性等因素，导致信号特征提取环节对故障诊断结果的判定产生较大影响。因此，寻求一种有效的故障诊断方法，对于确保设备处于良好工作状态具有重要意义。

分形理论是非线性科学中的一个活跃的数学分支，其研究对象是自然界和非线性系统中出现的不光滑和不规则的几何形体[1-2]，对应的定量参数是维数，在旋转机械[3]和电力电子电路故障诊断[4]及电路噪声分析[5]等故障诊断和电路相关领域都有了一定的应用和研究。电路中存在混沌现象是在理论和实践中证明了的不争的事实[6]。该文将其引入模拟电路信号分析领域，在探讨电路信号分形特征的基础上，利用它进行了电路故障的诊断，取得了良好的效果。

2 信号预处理与分形特征提取

电路运行状态与其各种故障征兆之间存在着因果联系，如电压、电流、温度、红外等，模拟电路的每一种故障状态就是一个样本，同一类故障出现的情况可能千差万别，但在特征上表现出共性，根据这些特征可以区别其他类型的故障。模拟电路中存在着不少非线性现象，在一定程度上可以用非整数的分形维数进行描述。如果电路偏离了正常的工作状态时，决定该电路状态的参数的吸引子就发生变化，相应的分形维数也要发生变化，即分形维数往往随着电路状态的改变而改变。因而可以把分形维数作为反映电路故障的特征量，通过电路分形维数的变化判断电路是否偏离了正常状态，是否出现了故障。

故障特征信息的提取，对于模拟电路故障诊断是非常重要的环节，分形和混沌是非线性领域的主要研究内容之一，它的发展对识别和预测复杂的非线性信号系统提供了新的方法论。分形理论用来刻画对象的不规则性和自相似性，在处理复杂非线性系统中具有独特的优点。运用分形理论，提取有用的诊断信息，不仅可以定性，而且可以定量地分析系统的工作状态，从而实现对模拟电路的故障诊断，提高对故障的识别和诊断能力。

2.1 分形盒维数

容量维数的定义，提出了一种测量分形的方法。取边长为ε的小盒子，把分形集覆盖起来。由于分形集内部有各种层次的空洞和缝隙，有些小盒子会是空的。计算有多少盒子不是空的，把这个数目记为N（ε）。然后缩小盒子的尺寸ε，计算得到的N（ε）自然要增大。根据前面的定义，只要在双对数坐标纸上画出logN（ε）对logε的曲线，其直线部分的斜率就是此分形集的盒子维数Db[7]，用式（1）表示为：

对于实际计算，只要分维小于二维或在二维附近，相空间维数也不高时，就是可行的。

2.2 模拟电路信号分形特征提取算法

根据盒维数的定义，网格越小计算结果越准确。分形维数受信号噪声影响较大，因此在计算分形维数时应对原始数据进行降噪处理。对于非线性系统，由于信号的频谱和噪声的频谱都表现为宽带连续谱，产生的噪声以传统的线性滤波方法则效果不佳。奇异值分解降噪[8]是基于噪声与系统信号对相空间轨道矩阵的奇异值的不同影响进行降噪的，能有效地去除非线性信号中含有的噪声。

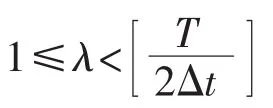
（1）相空间重构。用时延法重构相空间轨道矩阵：

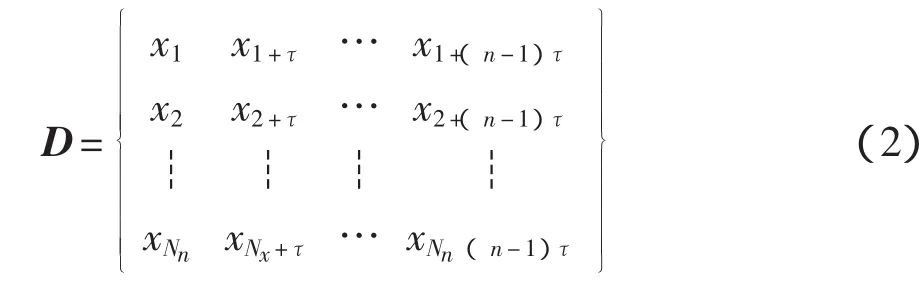
式中：τ——时间延迟；

n——嵌入维数；

n——重构相空间中向量的个数，Nn=N-（n-1）τ，Nn>>n。

（2）奇异值分解[6]。对轨道矩阵D进行奇异值分解（SVD）：

式中，S 是 DTD 的特征向量矩阵，∑=diag（λ1，λ2，…，λn），λ1，λ2，…，λn是矩阵D的奇异值，且有λ1≥λ2≥…λn≥0。噪声将会使所有的奇异值都大于零，假设矩阵的秩为k，则前k个奇异值要远大于其他奇异值。

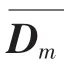
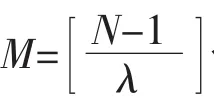
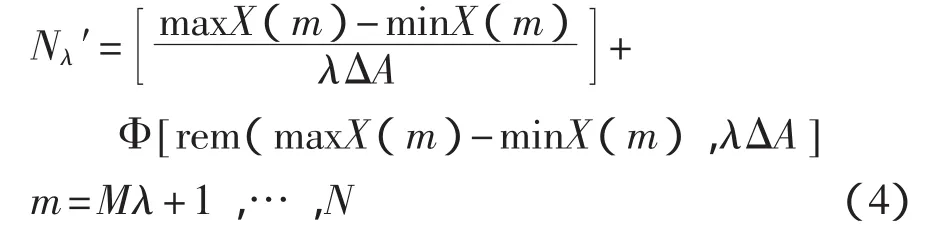
时间轴上的第 p（p=1，2，…，M）个等间隔区间内，与曲线相交的网格数Npλ为：

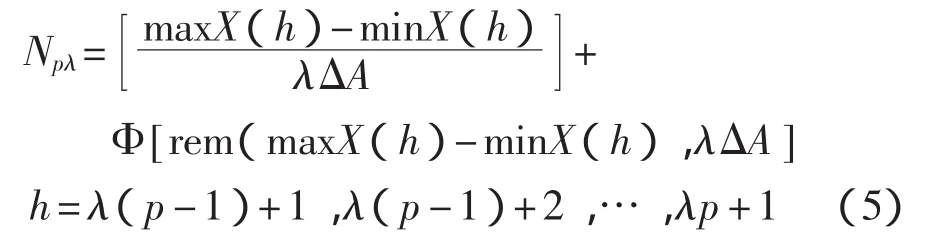
则在尺寸为λΔt×λΔA的矩阵网格下，与电路分形噪声波形曲线相交的总网格数Nλ为：

（5）最小二乘法计算盒维数。在k的取值范围内，去掉超过2和小于1的野点数据，改变λ值得到一系列 Nλ，再用最小二乘法对数据（Inλ，InNλ）进行线性方程回归，斜率就是盒维数，就得到电路分形噪声信号的盒维数。

3 以分形特征为输入量的故障诊断方法

模拟电路故障诊断的研究经历表明，利用单一信息、采用单一手段、基于单一理论的故障诊断方法是难以解决模拟电路故障诊断中的重重困难的，同样，单独一个测试节点所获取电路信息的分形特征也很难全面的表征电路状态。信息融合是将来自某一目标的多个传感器或多源的信息进行综合处理，从而得出更为准确、可靠的结论[9]，具有多信息量、多层次、多手段等优点，将其应用于模拟电路故障诊断，使诊断系统更为优越，可望解决以往诸方法中所普遍存在的由于诊断信息不足所带来的电路可测性难题以及由于元件容差所带来的问题。

3.1 分形维数隶属度的计算

对于信号的不同状态，以不同的采样周期进行求解分形特征，对于采样周期Δti，相应计算出的分形维数为dΔti，定义分形维数隶属度函数为z（Δti，dΔti），以此来表征采样周期Δti和分形维数dΔti之间的关系。以特定采样周期所获得的分形维数为中心维数点向两侧进行模糊化处理，按正态分布分配分形维数隶属度：

通过测试被诊断电路的多节点输出，求出每一节点在某故障条件下对应的分形维数隶属度值，以此作为模拟电路故障的分形诊断方法模式识别的特征分量。

3.2 神经网络信息融合步骤

电路运行状态与各种故障征兆间存在因果联系，但这种复杂关系很难直观表述，而神经网络可根据当前系统所接受的样本的相似性，确定分类标准，同时可以采用特定的学习算法获取知识，得到不确定性推理机制，非常适合信息融合技术的要求[10]。基于神经网络信息融合技术的模拟电路故障诊断方法将人工神经网络引入信息融合之中，属于特征层融合，同时结合模糊集合论进行故障判断。基于分形特征的模拟电路故障诊断原理框图如图1所示，按照故障诊断的要求以及测试分量的特点选取合适构建模拟电路故障诊断信息融合模型的BP网络模型，进行模拟电路运行状态诊断识别的诊断步骤为：

（1）依据获取的测试信息采用合适的学习方法，对构建的神经网络进行学习训练，确定网络的联接权值和联接结构，构建用于故障诊断的信息融合模型。

（2）所有节点的分形维数隶属度值矢量作为神经网络的输入，网络输出为融合后该症状属于各类故障的隶属度值矢量。在此过程中，充分利用利用神经网络的自学习和自组织功能，不断调整自己的结构和权值，满足测试条件不断变化的实时要求，提高故障诊断的可靠性。

（3）利用基于规则的判定原则进行故障决策。

故障决策一般遵守3条规则：隶属度函数值最大原则；隶属度函数值阈值原则；最大最小隶属度函数值之差阈值原则[11]。由于神经网络本身的特性，对于信息融合故障诊断而言，只要能获得足够精确的故障样本数据，合理地设计网络结构，就能得到准确的故障识别结果。

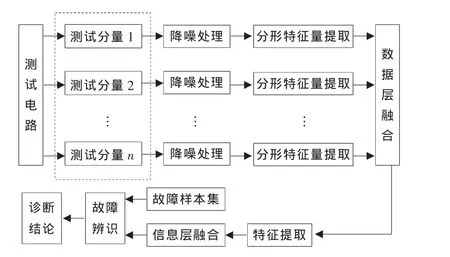
图1 模拟电路分形特征信息融合故障诊断原理框图

4 诊断实例

选取典型负反馈放大电路如图2所示，各参数见图2，电阻容差为5%，电容容差为6%。该电路虽然简单，但是节点较多，结构复杂，单靠经验分析排除故障存在困难。通过测试电路工作时所选支路的电流值和关键点电压值两方面的数据信息，提取分形维特征量，求出分形维数隶属度作为BP神经网络的输入，准确诊断故障元器件。

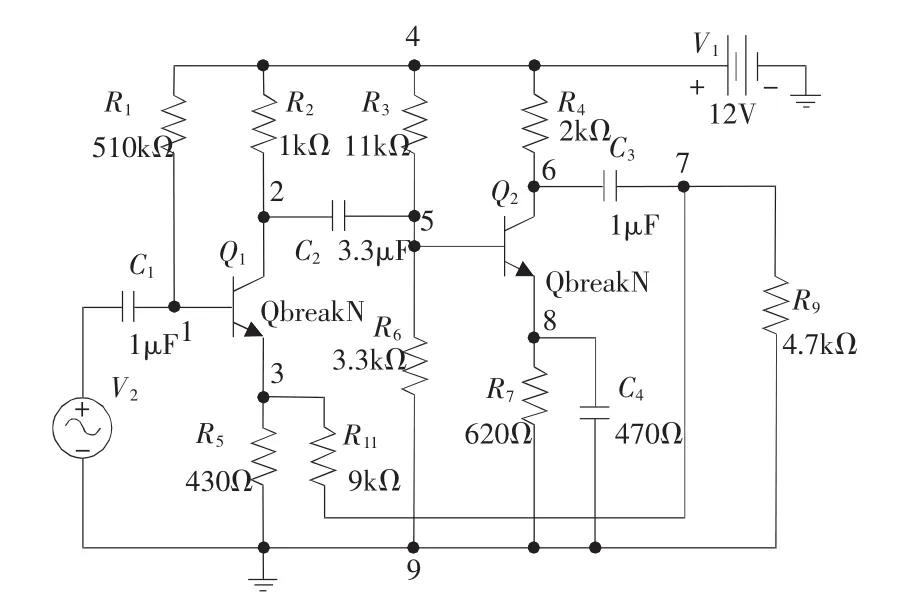
图2 负反馈放大电路

在此，以 Q1、Q2为例，分别称为元件 1、元件 2，神经网络训练期望输出为Db（Q1）、Db（Q2），实际输出为Db′（Q1）、Db′（Q2）。取节点3、8分别为元件1、2的工作电压测试点，选取故障元件隶属度函数值阈值为0.8，最大最小隶属度函数值之差阈值为0.6，运用信息融合方法进行故障诊断。该文采用的BP网络有4个输入，分别是各量测参数分形维属于故障的隶属度值；输出层节点数2即为故障模式的总数。综合考虑容错性和计算时间，隐含层节点数经过多次试验比较后选取10个隐层神经元，学习效率取0.01，期望误差为0.000 1，利用训练样本输入BP神经网络进行负反馈放大电路的故障诊断。表1为单一信息进行故障诊断时隶属度分配表及故障诊断结论，表2为对表1所属不同状态下的电压电流隶属度分别进行神经网络信息融合处理后获得的故障诊断结论。

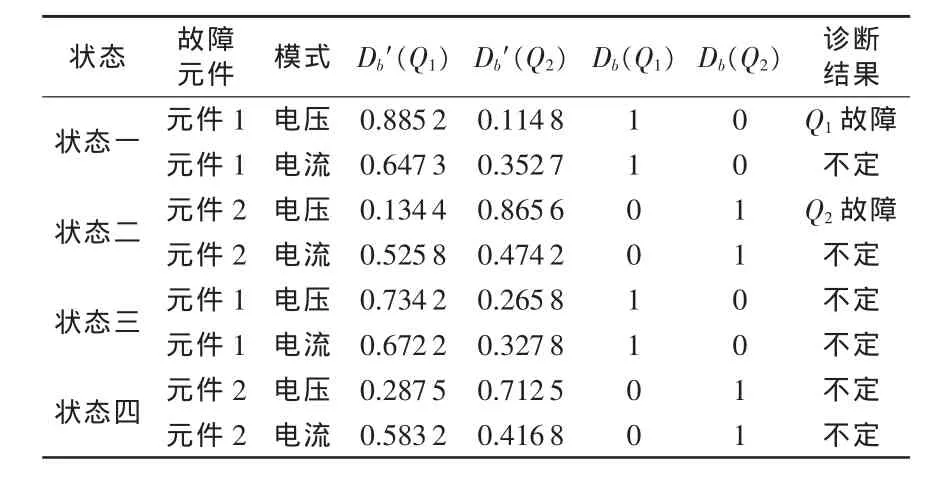
表1 单一信息诊断结论

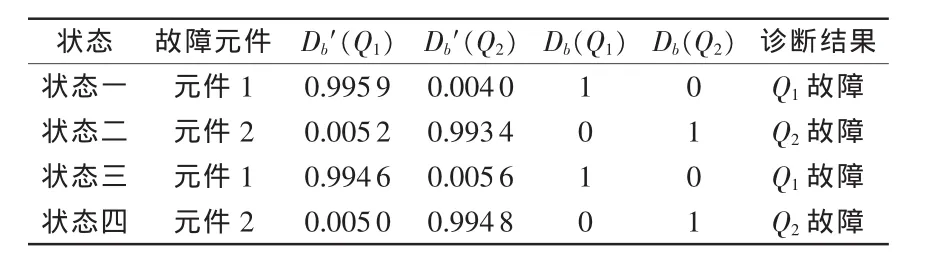
表2 BP神经网络信息融合诊断结论

融合后的隶属度值和单一的隶属度值相比，增加了实际故障元件的隶属度分配值，相对减少了其他元件的隶属度分配值，大幅度降低待诊断电路的不确定性。从表1中可以看出，对于设定的两种故障元件，有时候基于电压、电流所提取的分形维数故障隶属度值很相近，如果只用单一方式来识别，将无法确定故障元件。例如，元件2故障时，基于电流所提取的故障隶属度值比较接近，基于电压所提取的故障隶属度值也不能完全识别故障，因此无法单独判定故障元件，但经过信息融合后，元件2的隶属度值大为提高，且与元件1的隶属度值相差很大，就能准确判断故障元件为Q2。通过试验验证，故障识别的准确率达到了100%。

由此可见，基于分形的多信息融合故障诊断方法，使实际故障元件的隶属度值大为增加，待诊断电路的可分析性增强，故障元件定位的准确率大为提高。

5 结束语

该文研究了以分形特征为输入量的模拟电路故障诊断方法，结果表明，该方法有效地利用了电路系统在多种状态下的信息，将分形理论、神经网络和信息融合技术有机地结合起来，对模拟电路的输出响应数据提取分形特征后进行信息融合，合理地处理了模拟电路故障诊断时的不确定性，实现了故障诊断和定位。

[1]Paramanathan P，Uthayakumar R.Application of fractal theory in analysis ofhuman electroencephalographic signals[J].Computers in Biology and Medicine，2008，38（3）：372-378.

[2]李水根，吴纪桃.分形与小波[M].北京：科学出版社，2002.

[3]张 超，夏 立.发电机旋转整流器故障的分形和动态测度诊断[J].电机与控制学报，2009，13（1）：6-10.

[4]李 沁，张劲松.基于分形的电力电子电路故障诊断[J].电力电子，2007（11）：27-30.

[5]赵 健，雷 蕾，蒲小勤.分形理论及其在信号处理中的应用[M].北京：清华大学出版社，2008.

[6]马红光，韩崇昭.电路中的混沌与故障诊断[M].北京：国防工业出版社，2007.

[7]张济忠.分形[M].北京：清华大学出版社，1997.

[8]Shin K，Hammond J K，White P R.Iterative SVD method fornoise reduction oflow dimensionalchaotic time series[J].Mechanical Systems and Signal Processing，1999，13（1）：115-124.

[9]何 友，王国宏，陆大惍，等.多传感器信息融合及应用[M].北京：电子工业出版社，2007.

[10]丁 函，刘 青.神经网络与信息融合技术在内燃机车故障诊断中的应用 [J].现代电子技术，2008（23）：184-187.

[11]朱大奇，刘永安.故障诊断的信息融合方法[J].控制与决策，2007，22（12）：1321-1326.