Graphene条带的热稳定性研究

李爱华

(湖南科技学院 电子工程系，湖南 永州 425100)

0 引 言

Graphene是碳原子分布在二维蜂巢晶格点阵上的单原子层晶体，是一种理想的二维量子体系，成为当今凝聚态物理学和材料科学中最热门的研究课题之一。人们发现graphene体系具有一些奇特的电子性质：Dirac点附近的载流子的有效静质量为零，呈现相对论性质的特征，出现反常的量子霍尔效应等[1-6]。Graphene的电子性质与其几何构型有关，通过控制几何构型，可将其调制成金属和不同带隙的半导体。利用传统的电子束刻蚀技术可将 graphene制成电路和加工成特定形状[6]。Graphene对于高压、吸附、缺陷、掺杂等调制手段的响应与碳纳米管(CNT)有很多相似之处，在研究中可直接利用研究 CNT过程中所积累的经验，但graphene在应用性上优于 CNT，更容易与现代半导体工业结合，激起了人们对这种新型二维材料的广泛研究。

目前，实验上采用机械剥离[2,3]和外延生长[4,5]的方法已获得不同尺寸的graphene条带(GNRs)，人们对边沿用氢(或者氧、铯)饱和的GNRs和纯GNRs体系做了广泛的理论研究[7-13]。GNRs依据边沿碳原子的排列不同有两种经典的拓扑结构即锯齿型石墨带(ZGNR)和扶手椅型石墨带(AGNR)。根据最近邻π轨道紧束缚模型和第一性原理的研究，ZGNR一般体现金属性[7,8,9,10]，而AGNR随带宽的不同体现出金属或者绝缘体性质[7,8,9,11,12,13]。由于 GNRs边沿碳原子存在不饱和键，其性质很不稳定，容易与其它活性原子形成新的共价键而产生新型的复合物。而这类新型纳米复合材料将在纳米电子器件和自旋电子器件等方面具有重要的应用价值。

GNRs作为新颖的碳基纳米材料引起了人们极大的关注，它与石墨、CNT等一样具有非常好的热稳定性，石墨的熔化温度约为 4450K[14]，碳纳米管的熔化温度约4800K[15]，那么GNRs的熔化温度是多少？GNRs的熔化是否与条带的带宽、边界构型有关呢？GNRs是一种性能优越的新型功能材料和结构材料，有广泛的应用前景，正确认识GNRs的热稳定性，是我们探索GNRs高温应用的前提和基础。在本文里，我们将采用分子动力学模拟方法分别研究不同宽度的ZGNR和AGNR的热稳定性，依据Lindemann判据探讨GNRs的热稳定性，取得一系列有意义的结果。我们发现作为大块固体熔化的判据Lindemann指数qL=0.1~0.15[16]对 GNRs不适用。我们依据Lindemann指数曲线在熔化点附近的变化趋势得出ZGNR和AGNR的整体熔化温度分别为5000K~5500K和4500K~5000K，适用于纳米颗粒、聚合物和碳纳米管的熔化临界 Lindemann指数qC=0.03~0.05[17]，同样适用于对GNRs发生熔化的判定，且GNRs的熔化总是从边缘开始。

1.子动力学模拟与势模型

分子动力学模拟是研究复杂微观系统的有力工具，不仅可以直接模拟许多物质的宏观凝聚特性，得出与实验结果相符合或者可比拟的计算结果，而且可以提供微观结构，粒子运动以及它们和物质宏观性质关系的明确图像。模拟结果准确与否的关键在于系统内原子之间相互作用势函数的选取。

本文采用正则系综(NVT)进行分子动力学模拟，C-C原子间的相互作用势由多体Tersoff势[18]描述， Tersoff势能比较好地描述碳结构的性质[19]。运动方程的数值积分使用 5值Gear预测-矫正算法，截断半径为1 nm，温度控制使用速度标度法，GNRs周围留出足够的真空层，使用周期性边界条件，模拟步长为0.5 fs,模拟步数20万步(100 ps)。为量化GNRs的熔化程度，我们引进Lindemann指数。原子数为N的系统，在模拟温度T下，每个原子的Lindemann指数和整个系统的平均Lindemann指数被定义为[17]

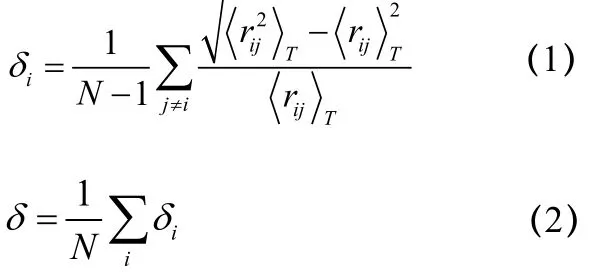
Yaoqi Zhou等人[17]用分子动力学模拟方法研究了纳米颗粒和聚合物熔化与预熔化转变的 Linde-mann判据，KaiWang Zhang等人[15]用分子动力学模拟方法研究了碳纳米管的熔化行为，均得出 Lindemann指数熔化的临界值为0.03~0.04。我们知道，在系统未达到熔化温度以前,Lindemann指数会随温度的增加呈线性缓慢增大，在临近熔化温度时，Lindemann指数对温度的增加非常敏感，会偏离原来的线性关系迅速增大。我们依据Lindemann指数曲线在熔化点附近的变化趋势得出GNRs 的熔化温度。

2.算模拟结果与讨论

2.1.GNR的热稳定性研究

首先考虑具有相同带长(4.919nm)，不同带宽(NZ)的ZGNR的热稳定性。ZGNR带宽NZ的计算方法如图1所示。对 ZGNR在不同温度下进行分子动力学模拟。不同温度下的模拟结果表明，不同带宽的 ZGNR在各种温度下都会不同程度地发生扭曲变形，扭曲现象表明 ZGNR具有良好的柔韧性，即使出现较大的变形也不发生断裂。温度越高扭曲变形越大，C-C键长被拉伸地越长。研究发现，在 5000K温度下ZGNR仍保持其六方网格的完整性。

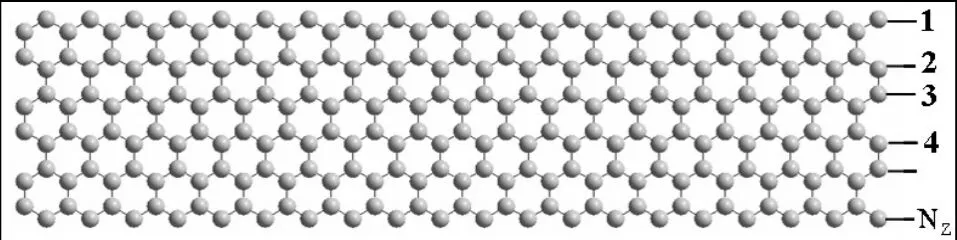
图1.GNR带宽的定义示意图

计算不同带宽的ZGNR在不同温度下的平均Lindemann指数，如图2所示。从图2中能清晰地看出，NZ=2时，ZGNR的平均 Lindemann指数突变点对应的温度值大约在 4800K。NZ=4，6，8时，ZGNR的平均Lindemann指数突变点对应的温度值基本保持在5000K左右。在5000K温度下，Lindemann指数随着温度的增加而缓慢地线性增大，并随着带宽的增大，Lindemann指数曲线的斜率逐渐减小。从5000K到更高的温度，Lindemann指数开始背离原来的线性增长关系，到5500K完全变成急速增长的行为。从四种带宽的 ZGNR的平均Lindemann指数可以知道，随着条带宽度的增加，ZGNR的熔化温度变化稍高，起伏范围在5000K左右。

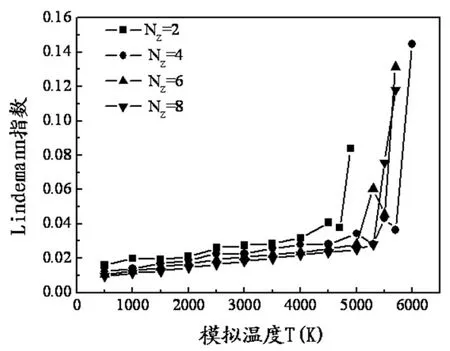
图2.同带宽ZGNR的平均Lindemann指数与温度的关系

下面我们考虑带长(9.8384nm)，带宽(NZ=6)的ZGNR(C480)在不同温度下进行分子动力学模拟。不同温度下的模拟结果也表明，ZGNR在各种温度下都会不同程度地发生扭曲，温度越高变形越大，C-C键长越长，ZGNR在5000K温度下仍保持其六方网格的完整性。

图3.GNR-C480的平均Lindemann指数随温度变化曲线

计算ZGNR-C480的平均Lindemann指数，其与模拟温度的关系如图 3所示。图 3左上角小图模拟温度分别为1000K、4000K和5300K条件下的ZGNR模拟结果。从图3中能清晰地看出 ZGNR平均 Lindemann指数在模拟温度5300K左右发生了明显的变化。5300K以下，Lindemann指数随温度增加缓慢地线性增大，说明原子在初始位置附近做典型的热振动。从5300K到更高的温度，Lindemann指数开始背离原来的线性增长关系，到 5500K完全变成急速增长的行为。对比具有相同带宽(NZ=6)的ZGNR，发现将带长增长时其熔化温度会升高一点点。同时还发现随着模拟温度的增加，ZGNR边缘首先出现C键的断裂，接着断裂的C键发生重构，熔化是从ZGNR的边缘开始的。

通过对ZGNR的热稳定性研究，我们发现，ZGNR的熔化温度在5000K左右，随着ZGNR条带的增长，带宽NZ的增大，熔化温度升高，并且熔化是从条带边缘开始的。

2.2.GNR的热稳定性研究

考虑具有相同带长(5.964nm)，不同带宽(NA)的 AGNR的热稳定性。AGNR带宽 NA的计算方法如图 4所示。对AGNR在不同温度下进行分子动力学模拟。不同温度下的模拟结果与 ZGNR的模拟结果类似。研究表明，不同带宽的AGNR在各种温度下也都会不同程度地发生扭曲，温度越高扭曲越剧烈，条带变形越大，C-C键长也越长。AGNR在4500K温度下仍保持其六方网格的完整性。

图4.GNR带宽的定义示意图

将不同带宽(NA=3，5，7，9)的AGNR在不同温度下模拟，计算出不同条带的平均Lindemann指数，其与温度的关系如图 5所示。从图 5中能清晰地看出，AGNR的平均Lindemann指数突变点对应的温度值基本保持在 4500K左右。4500K以下，Lindemann指数随温度增加缓慢地线性增大，并且随着带宽的增加Lindemann指数曲线的斜率逐渐减小。从4500K到更高的温度，Lindemann指数开始背离原来的线性增长关系，到 5000K完全变成急速增长的行为。从图5中还能发现，模拟温度4500K左右正好对应0.04δ≈，这与纳米颗粒和聚合物的熔化判据基本一致。带宽的变化对AGNR熔化的影响并不是很明显。

图5.同带宽AGNR的平均Lindemann指数与温度的关系

我们将带长(8.9460nm)，带宽(NA=11)的 AGNR(C462)在不同温度下进行分子动力学模拟。计算 AGNR的Lindemann指数，其平均Lindemann指数与模拟温度的关系如图6所示。图6左上角小图模拟温度分别为1000K、3500K和4800K条件下AGNR的模拟结果。从图6中能清晰地看出AGNR平均Lindemann指数在模拟温度4800K左右发生了明显的变化，4800K以下，Lindemann指数随温度增加缓慢地线性增大，从4800K到更高的温度，Lindemann指数开始背离原来的线性增长关系，到 5000K完全变成急速增长的行为。温度4800K时的Lindemann指数突变点正好对应≈ 0 .03~0.05，这也与纳米颗粒和聚合物的熔化判据一致。同时还发现AGNR条带增长增宽后，其熔化温度会随之升高，并且条带边缘首先出现 C键的断裂，进而出现 C键的重构，这与ZGNR一样，AGNR也是从条带边缘开始熔化的。

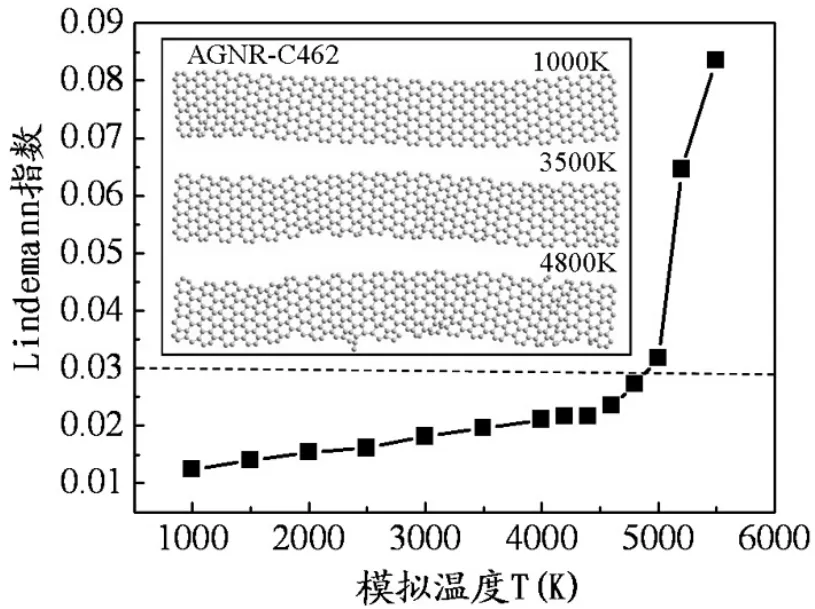
图6.GNR-C462的平均Lindemann指数随温度变化曲线

3. 结

采用分子动力学模拟方法对不同带宽、带长的 ZGNR和AGNR模型在不同温度下进行模拟，以Lindemann指数作为条带熔化的判据。根据 ZGNR和 AGNR的平均Lindemann指数与模拟温度的关系，可以推定ZGNR的整体熔化温度约为5000K~5500K，AGNR的整体熔化温度约为4500K~5000K，并且条带的熔化受其带宽带长的影响。这两个熔化温度略高于石墨的熔化温度 4450K和碳纳米管的熔化温度4800K，并且ZGNR的Lindemann指数的温度转变点比AGNR的要高些，说明ZGNR的热稳定性比AGNR相对要好些。在熔化温度以上，ZGNR和AGNR边沿的C-C键均出现大量的断裂，断裂的 C键发生重构，形成五边形和七边形。ZGNR和AGNR的熔化都是从条带边沿开始。

[1]Novoselov K S, Geim A K, Morozov S V, et al. Electric Field Effect in Atomically Thin Carbon Films[J]. Science,2004, 306: 666-669.

[2]Novoselov K S, Geim A K, Morozov S V, et al.Two-dimensional gas of massless Dirac fermions in graphene[J]. Nature (London), 2005, 438: 197-200.

[3]Zhang Y, Tan Y W, Stormer H L, et al. Experimental observation of the quantum Hall effect and Berry's phase in graphene[J]. Nature (London), 2005, 438: 201-204.

[4]Berger C, Song Z M, Li X B, et al. Electronic confinement and coherence in patterned epitaxial graphene[J]. Science,2006, 312: 1191-1196.

[5]Berger C, Song Z, Li T, et al. Ultrathin Epitaxial Graphite:2D Electron Gas Properties and a Route toward Graphene-based Nanoelectronics[J]. J. Phys. Chem. B, 2004,108: 19912-19916.

[6]Novoselov K S, Jiang D, Schedin F, el at. Two-dimensional atomic crystals[J]. Pro. National. Aca. Sci, 2005, 102(30):10451-10453.

[7]Fujita M, Wakabayashi K, Naka K, et al. Peculiar localized state at zigzag graphite edge[J]. J. Phys. Soc. Jpn, 1996, 65:1920-1923.

[8]Nakada K, Fujita M, Dresselhaus G, et al.Edge state in graphene ribbons: Nanometer size effect and edge shape dependence[J]. Phys. Rev. B, 1996, 54(24): 17954-17961.

[9]Sasaki K, Murakami S, Saito R. Gauge field for edge state in graphene[J]. J. Phys. Soc. Jpn, 2006, 75(7): 074713(8).

[10]Sasaki K, Murakami S, Saito R. Stabilization mechanism of edge states in graphene[J]. Appl. Phys. Lett., 2006, 88(11):113110(3).

[11]Wakabayashi K, Fujita M, Ajiki H, et al. Electronic and magnetic properties of nanographite ribbons[J]. Phys. Rev.B, 1999, 59(12): 8271-8282.

[12]Ezawa M. Peculiar width dependence of the electronic properties of carbon nanoribbons[J]. Phys. Rev. B, 2006,73(4): 045432(8).

[13]Brey L, Ferting H A. Electronic states of Graphene nanoribbons studied with the dirac equation[J]. Phys Rev B,2006, 73:235411-235415.

[14]Son Y W, Cohen M L , Louie S G. Half-metallic Graphene nanoribbons[J]. Nature, 2006, 444: 347-349.

[15]Zhang K W, Stocks G M, Zhong J X. Melting and premelting of carbon nanotubes[J]. Nanotechnology, 2007,18:2857031-2857035.

[16]Lindemann F A. The calculation of molecular vibration frequencies[J]. Phys Z, 1910, 11: 609-612.

[17]Zhou Y, Karplus M, Ball K D, et al. The distance fluctuation criterion for melting: Comparison of square-well andMorsepotentialmodelsforclustersand homopolymers[J]. J Chem Phys, 2002, 116: 2323-2329.

[18]Tersoff J. Modeling solid-state chemistry: interatomic potential for multicomponent systems[J]. Phys Rev B, 1989,39: 5566-5568.

[19]Schelling P K, Keblinski P. Thermal expansion of carbon structures[J]. Phys Rev B, 2003, 68: 354251-354257.