渗透剂的分子体积和极性表面积分率对胰凝乳蛋白酶抑制剂2热稳定性的影响

刘夫锋 纪 络 董晓燕

(天津大学化工学院生物化工系,天津 300072; 天津大学系统生物工程教育部重点实验室,天津 300072)

渗透剂的分子体积和极性表面积分率对胰凝乳蛋白酶抑制剂2热稳定性的影响

刘夫锋 纪 络 董晓燕*

(天津大学化工学院生物化工系,天津 300072; 天津大学系统生物工程教育部重点实验室,天津 300072)

渗透剂对蛋白质的稳定能力不仅与其极性表面积分率(fpSA)有关,而且也与其分子体积(V)密切相关.因此对于渗透剂稳定蛋白质能力的分析,需要同时考虑渗透剂的fpSA和V.为了考察渗透剂的fpSA和V对稳定蛋白质能力的影响,本文以胰凝乳蛋白酶抑制剂2(CI2)为模型蛋白,首先利用分子动力学模拟,考察了数种典型渗透剂对CI2热稳定性的影响;并根据模拟数据计算得到了渗透剂影响蛋白质热稳定性的一维结构参数;然后利用统计学双参数拟合,同时引入渗透剂的fpSA和V,建立了用于分析渗透剂稳定蛋白质能力的模型;最后利用模型分析了渗透剂的fpSA和V与其稳定蛋白质能力的关系.研究发现:利用分子动力学模拟结果定义并计算得到的一维结构参数能够较好地描述在热变性条件下渗透剂对CI2的稳定能力;所建立的模型能够很好地分析渗透剂对蛋白质的稳定能力;并且由于V和fpSA二次项的引入,可大大提高仅以fpSA为参数的模型的精度;另外,渗透剂对蛋白质的热稳定能力与其V成正比;由于拟合公式中引入了fpSA二次项,在fpSA小于0.7时,fpSA与渗透剂的稳定能力呈现负相关,但当fpSA大于0.7时,其与渗透剂的稳定能力反而呈现正相关.

分子动力学模拟; 蛋白质稳定性; 渗透剂; 极性表面积分率; 分子体积

蛋白质在一些极端条件(如极端的低温和高温、干燥以及高浓度的脲和盐的环境)下会丧失原有的生物活性[1],但一些渗透剂能够增强蛋白质在上述极端环境下的结构稳定性,从而防止蛋白质失活[2-3].目前普遍认为渗透剂分子的优先排阻作用是渗透剂稳定蛋白质的主要原因[4-5].这是由于保护性渗透剂分子和水分子与蛋白质的亲和力不同,使其相互作用优先级不同.蛋白质优先结合水分子,而排除渗透剂分子,从而使这些渗透剂分子在蛋白质表面发生排阻.因而相对溶液主体,蛋白质表面水分子增多而渗透剂分子减少.另外,渗透剂分子与蛋白质的相互作用使其化学势升高,是热力学不利的过程,其化学势增加与蛋白质的溶剂暴露程度成正比.由于变性态蛋白质具有更大的溶剂暴露程度,同时渗透剂的加入又可使变性态蛋白质的化学势升高程度更大,因此使变性态蛋白质变得更加不稳定,从而使自然态蛋白质相对更加稳定.即保护性渗透剂的优先排阻作用使蛋白质变性态更加不稳定,从而使平衡向折叠态移动来达到稳定蛋白质自然结构的作用[6-7].

研究结果显示,与蛋白质存在于纯水溶液相比,蛋白质在保护性渗透剂溶液中会产生正的转移自由能(ΔGtr),且实验测得的ΔGtr值与其保护能力正相关[8-9].此外Bolen等[10]认为,由于渗透剂主要通过极性基团与蛋白质的主链发生作用,因此极性表面渗透剂分布越少就越容易被蛋白质所排阻,从而使其 ΔGtr值增加,稳定能力更强,如氧化三甲胺(TMAO)和甜菜碱等.为了进一步辨析造成渗透剂稳定能力差别的原因,他们又分别计算了常见渗透剂分子的极性和非极性基团表面积,并定义了极性表面积分率(fpSA),即:极性基团表面积占分子总表面积的比例.通过将不同渗透剂的fpSA与ΔGtr进行线性拟合,发现二者呈反比关系,且相关系数为0.81.

然而,很多实验和模拟研究表明,如蔗糖和海藻糖等多羟基类渗透剂对蛋白质的稳定具有很好的效果[11-14],可是它们的fpSA却较大.作者进一步分析发现多羟基类渗透剂(甘油,山梨醇,海藻糖和蔗糖)稳定蛋白质的能力与其fpSA呈正相关,这与Bolen的研究结果不一致.说明渗透剂稳定蛋白质的能力与fpSA不是简单的线性关系,可能存在复杂的函数关系.另外,我们[15]前期的研究表明,多羟基类渗透剂稳定蛋白质的能力与其分子体积(V)呈正相关.因此我们认为fpSA只能代表渗透剂分子中极性和非极性表面积的相对比例,而V不仅决定了渗透剂分子的表面积,而且其对应的空间位阻效应与渗透剂优先排阻作用也有直接关系.所以忽略渗透剂的V会造成渗透剂对蛋白质稳定能力分析的误差.

由于胰凝乳蛋白酶抑制剂2(CI2)具有结构典型、分子体积小等优点,常用于实验[16-17]和模拟研究[18-21].此外,研究表明CI2的热变性中点温度(Tm)高于353 K[22].众所周知,模拟温度越高,蛋白质热变性速度越快,从而可以大大减少计算时间.在363 K下进行模拟能够使CI2在水溶液中尽快变性,这种方法在分子动力学模拟研究蛋白质变性的文献中经常使用[18,23].同时,该模拟温度低于水的沸点(373 K),从而使该模拟具有一定的生理意义.因此本研究以CI2为模型蛋白,首先运用分子动力学模拟(MD)[24]考察高温(363 K)条件下,CI2在典型渗透剂(TMAO,甜菜碱,肌氨酸,脯氨酸,乙醇,甘油,山梨醇,海藻糖和蔗糖)溶液中的结构变化情况.由于通过MD所得的结构参数仅能反应蛋白质分子某一方面的结构变化,在此本研究借鉴了Daggett等[25]的方法,计算能够反应CI2结构特性的一维参数,并由此获得基于模拟结果的渗透剂对蛋白构象的保护能力参数(PMD),将其作为模型的响应量;作为对比,将基于实验结果的ΔGtr值也作为响应量;同时将fpSA和V作为自变量,运用统计学中的双参数拟合建立准确的模型.利用所建模型分析上述渗透剂参数与稳定蛋白质能力的关系,以期加深理解渗透剂稳定蛋白质的机理,并为理性设计蛋白质复性助剂提供有益的指导.

1 计算方法

1.1 体系构建

CI2的初始结构从蛋白质数据库(protein data bank,PDB)中获得,PDB号为1YPC.TMAO,甜菜碱,肌氨酸,脯氨酸,乙醇,甘油,山梨醇,海藻糖和蔗糖的结构式如图1所示.它们的拓扑结构通过PRODRG2服务器(http://davapc1.bioch.dundee.ac.uk/ cgi-bin/prodrg_beta)获得[26].

首先将CI2放入一个立方体盒子(8 nm×8 nm×8 nm)中,然后将154个渗透剂分子随机放入该盒子,并与蛋白质保持一定的距离.随后将盒子中加满水,并去除与蛋白质或渗透剂重叠的水分子.采用三次能量最小化模拟优化该体系:首先,固定蛋白质和渗透剂分子的结构和位置不变,仅让水分子的结构和位置发生变化;其次,仅固定蛋白质分子的结构和位置,使渗透剂和水分子的结构和位置发生变化;最后,使所有的分子都可以自由运动.这三步优化都通过1000个循环的最陡下降法和共轭梯度法来完成.

1.2 分子动力学模拟

将上述优化好的体系进行分子动力学模拟,渗透剂的浓度选择参考文献中所用的0.5 mol·L-1[27-28],每个体系模拟时间为20 ns.各模拟体系的详细信息如表1所示.从图1可以看出,渗透剂分子的大小不同,在相同浓度下(一定的盒子体积中)相同数量的渗透剂所占体积不同,这样就导致模拟盒子中水分子的数量不同.如,体积最小的乙醇体系中,共有16248个水分子,而体积最大的蔗糖体系中的水分子个数仅为14375(表1).模拟过程中,为了使模拟结果更具有代表性,对相同温度下的同一体系通过改变动力学模拟参数中的随机数,使体系中各原子获得不同的初始速度,得到了不同的模拟轨迹,这些模拟结果均具有相似性.

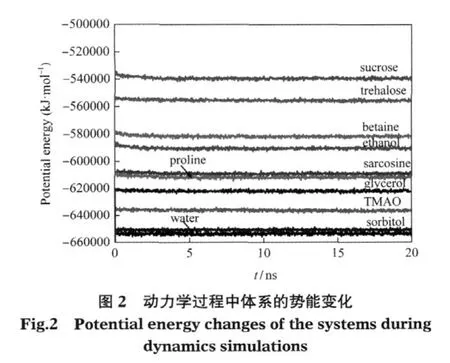
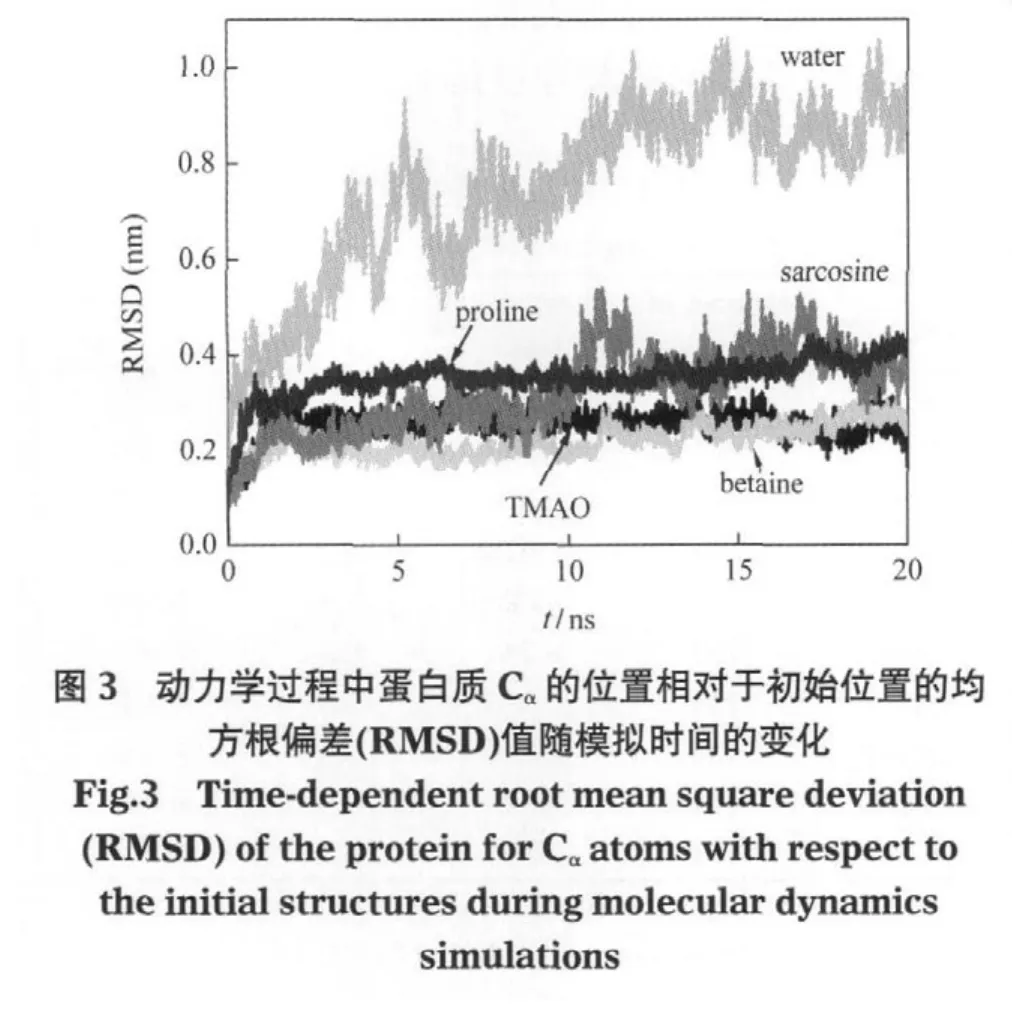
利用体系的势能在模拟过程中保持稳定来说明体系已经达到平衡,是很多文献常用的方法[29-30].本文首先也观察了体系的势能变化曲线(图2),从该图可以看出,体系的势能经过最初的急剧降低后趋于稳定,所有模拟体系的势能在最后5 ns的模拟过程中基本不变,说明体系已经达到平衡.随后,又分析了表示蛋白质结构变化的参数——均方根偏差(RMSD)随模拟时间的变化(图3).四种多羟基类渗透剂的模拟数据可参见我们前期发表的文章[15].结果表明,蛋白质Cα的RMSD在最后5 ns内达到了平衡.因此,用最后5 ns的模拟数据进行分析具有代表性.此外,为保证数据可信,每个体系的模拟均重复了3-4次,并将这些结果取平均值进行考察.

表1 模拟体系的参数Table 1 Parameters of simulation systems

本文采用GROMACS 3.3.1分子动力学模拟软件[31],水分子采用SPC模型,选择GROMOS96力场[32]来表述分子之间的势能.利用Lennard-Jones函数计算范德华作用力,非键截断距离设为1.4 nm,非键作用原子列表每4个步长更新一次;用LINCS算法约束所有原子的键长,利用particle mesh Ewald方法[33]计算长程静电相互作用,格点宽度设为0.12 nm;采用Verlet蛙跳算法[34]对每一步的运动方程进行求解,经过积分得到新时刻各原子的坐标,积分步长为2 fs,模拟过程中采用周期性边界条件.所有模拟均在等温等压系综下进行,温度为363 K,通过Berendsen方法[35]控制温度,时间常数设为0.1 ps.压力为1.01×105Pa,压力控制采用 Berendsen方法,压力耦合常数为0.5 ps.所有分子动力学模拟计算均在曙光TC2600刀片服务器(每刀片包括4路4核的AMD Opteron 8347HE CPU和8 G内存)上完成(Dawning,Tianjin,China).

1.3 数据分析方法

CI2的α-碳原子的均方根偏差、蛋白质分子内氢键、疏水溶液接触面积、β折叠(β-sheet)、α螺旋(α-helix)、分子内天然接触个数和侧链接触个数这七个参数,都利用GROMACS软件所自带的程序计算获得.渗透剂的分子体积利用大型药物分子设计软件SYBYL 6.92计算.模拟过程中采用VMD软件[36]显示和获取CI2分子的典型构象.

参照Daggett等[25]的方法,按照式(1)计算任意时刻CI2分子的这些参量的平均偏差:

其中p为所选用的状态参量,这里p的总数为7;i为模拟过程中任一时间点所代表的典型构象,s为参比状态(这里为自然态N,此时i=1,即为初始时刻);xp,i代表CI2在i时刻的第p个状态参量值.〈 Ri-N 〉代表i时刻CI2分子相对参比状态的平均偏差程度,其值越大表示变性效果越强,例如自然状态的〈 Ri-N 〉等于0.然后利用式(2)将〈 Ri-N 〉进一步转化为衡量CI2结构性质的一维结构参数χ,即χ=1时表示此时刻蛋白质结构为天然折叠态,而χ=0时则为完全变性态:

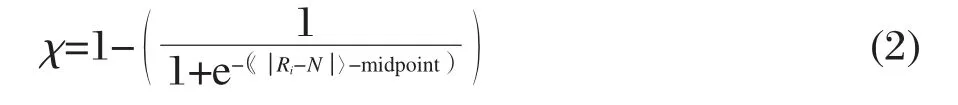
其中中点值(midpoint)由CI2在纯水溶液中的变性过程决定,即通过分析纯水溶液中CI2的〈 Ri-N〉分布,当分布处于局部最小值并使得相应χ值为0.5时的〈 Ri-N 〉就确定为midpoint值.对最终5 ns的χ值取平均〈(χ〉).最后,利用式(3)定义渗透剂对其构象的保护能力(PMD)为该溶液的〈χ〉相比于纯水溶液中的〈χ〉w的相对偏差,

作为对比,本文首先仅将fpSA作为自变量(x),分别以PMD和ΔGtr作为响应量(y)进行线性拟合,其拟合公式如式(4)所示:

然后将fpSA和V同时作为自变量(x),分别以PMD和ΔGtr作为响应量(y),进行双参数拟合,同时考虑交叉项和二次项的拟合公式如式(5)所示:

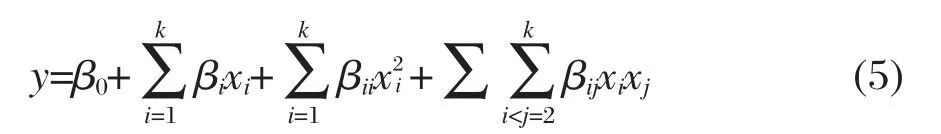
β0为常数项,而k=2.拟合过程中只将线性项和显著程度大于0.9(即该项不能解释的数据少于总量的10%)的二次项保留在最终的拟合公式中.

2 结果和讨论

2.1 不同渗透剂对CI2二级结构的影响

模拟初始时刻,各溶液体系中的CI2蛋白均处于自然状态,如图4A所示;经过20 ns的模拟,在不同渗透剂溶液中的模拟最终时刻CI2的分子构象分别如图4(B-F)所示.可以看出,在纯水溶液中,CI2的结构基本被破坏,表现为其α螺旋和β折叠区域基本上被转角和无规则卷曲的二级结构所取代(图4B).而在渗透剂溶液中,CI2的自然结构得到了不同程度的稳定.例如在肌氨酸和脯氨酸溶液中,模拟结束时CI2自然结构中的β折叠区域得到了很好的维持(图4C和4D);而在含有TMAO和甜菜碱的溶液中,CI2构象中的β折叠和α螺旋都得到了较好的保护(图4E和4F).同样如海藻糖,蔗糖等多羟基类渗透剂也具有不同的保护能力,但其他化合物如乙醇对蛋白质热稳定性基本没有抑制能力,这些模拟数据可参见我们前期发表的文章[15].

2.2 CI2的一维结构参数在不同溶液中的变化

由于图4只能显示模拟最终时刻的蛋白构象.虽然蛋白质结构的其他性质能够由均方根偏差(图3)、疏水溶液接触面积等结构参数表示出来,但如何用单一参数定量化精确化地表示某一时刻CI2的结构特点,进而定义不同渗透剂稳定蛋白质能力的差别,是非常重要的.

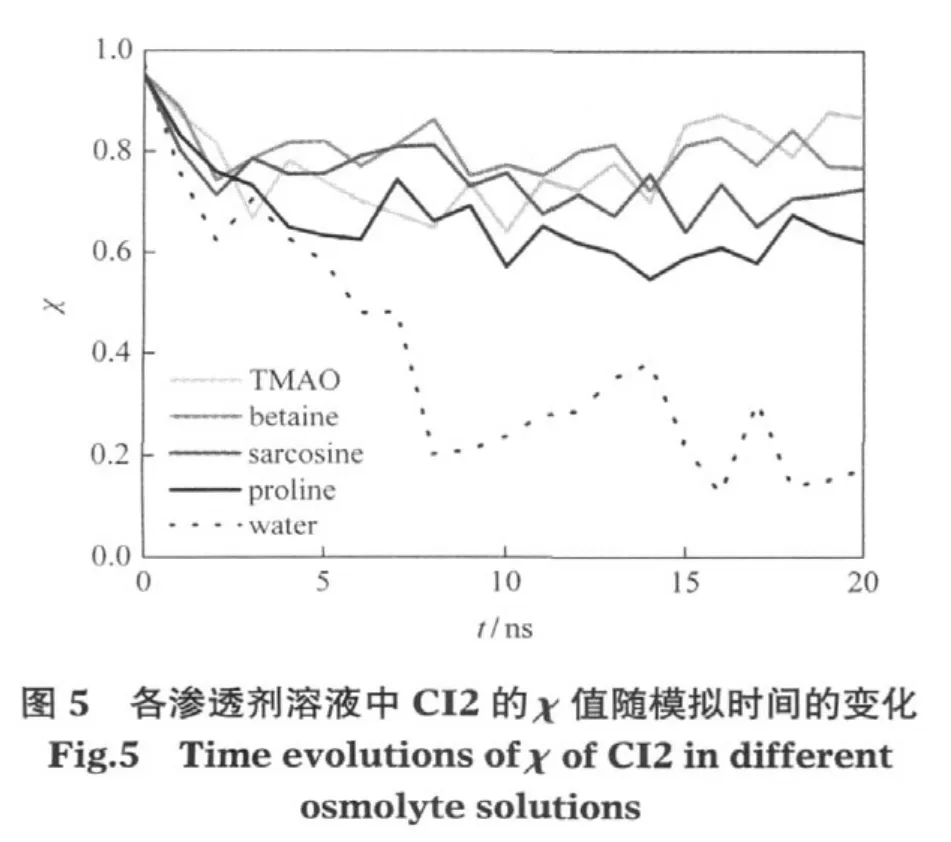
本研究中,作者首先利用分子动力学模拟所得数据,根据式(1)和(2)计算得到各溶液中CI2的一维参数χ的变化情况,并将其作为衡量CI2分子结构性质的反应坐标,以模拟时间为横坐标,做出CI2分别在纯水溶液和4种渗透剂溶液中的χ值随模拟时间的变化趋势(图5).从该图可以看出,纯水溶液中CI2的χ值在模拟初期急剧下降,在最后2 ns内基本稳定在0.2左右;而在渗透剂溶液中,虽然初始阶段χ值也存在一定程度的下降,但是平衡阶段的χ值却比纯水溶液中的高,这表明了渗透剂对CI2分子结构都有稳定效果.通过比较,可以发现TMAO和甜菜碱对CI2的稳定效果最好,其χ值保持在0.8左右;而肌氨酸和脯氨酸溶液的稳定效果就稍差一些,其χ值约在0.6到0.7之间,这与图4的结论是一致的.同样CI2在海藻糖、蔗糖等多羟基类渗透剂溶液中的χ值与它们各自的保护能力也呈很好的相关性,这些模拟数据可参见我们前期发表的文章[15].由于这里χ的变化趋势基本体现了纯水溶液中的变性趋势,以及渗透剂溶液中的稳定效果,并且与之前文献有着相似的结果[25],因此认为这一定义和计算是可信的,可以用其计算其他相应的参数.为了更精确地表示不同渗透剂对CI2热变性的保护能力和下一步数学建模的需要,我们根据式(3)进一步定义了渗透剂对CI2结构的保护能力参数(PMD).

2.3 对渗透剂稳定能力的双参数拟合

表2列出了各渗透剂分子的性质:如fpSA、V以及各种渗透剂对CI2的保护能力参数(PMD和ΔGtr).其中fpSA、V及PMD值为计算结果,而ΔGtr为文献中的实验值[10].可以看出,甲胺类物质的fpSA普遍较小,而多元醇类的fpSA则较大,这是由于它们含有多个羟基所造成的,这与文献[10]中报道的一致;同样V作为体积的量度也能较好地反映渗透剂分子体积的相对大小趋势,例如含有两个六元环的蔗糖和海藻糖的V最大,而TMAO、肌氨酸的V最小(如图1所示).基于分别从模拟和实验角度来衡量渗透剂稳定能力的考虑,在此将PMD和ΔGtr进行线性拟合,如图6所示.二者的相关系数为0.81,说明通过分子动力学模拟得到的渗透剂对蛋白质的稳定能力的趋势与实验测量的结果是一致的,这也从另一个方面证明了模拟结果的可信度.

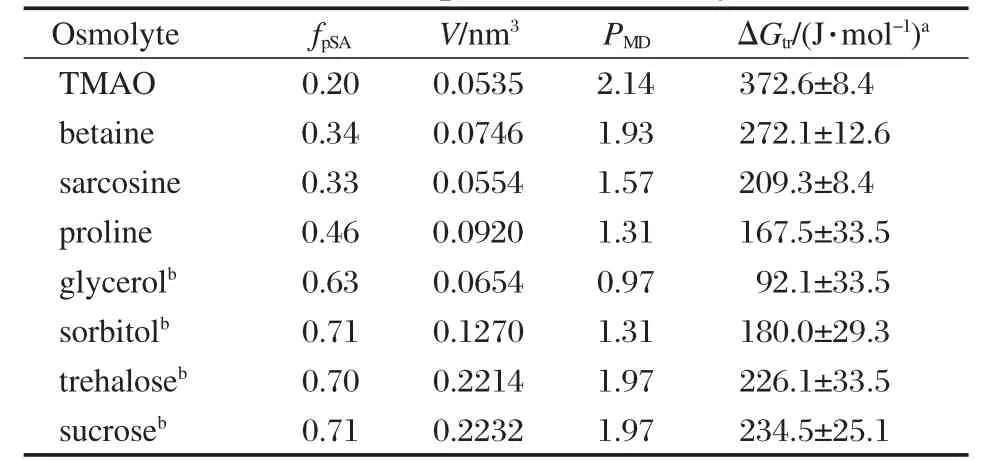
表2 渗透剂的性质Table 2 Properties of osmolytes

为了分析fpSA与渗透剂稳定能力之间的关系,首先只将fpSA与基于MD模拟结果计算所得到的PMD按照式(4)拟合,得到预测公式(线性相关系数R2=0.10):

然后将fpSA和V同时作为自变量,与PMD按照式(5)进行双参数拟合,得到预测公式(R2=0.94)为:

如利用PMD值与Pcal值之间的R2表示该模型的拟合精度,可以看出,单独采用fpSA作为自变量拟合,其线性相关系数仅为0.10.这说明至少在本研究范围内,单独用渗透剂分子的fpSA并不能很好地衡量它们对蛋白质的热稳定能力.相反,若将渗透剂分子体积V和fpSA二次项同时引入,即可使线性相关系数从0.10提高到0.94.这不仅说明渗透剂的分子体积与蛋白质的热稳定能力密切相关,也证明作者之前的分析,即若同时考虑渗透剂分子体积和fpSA二次项可大大提高模型的精度和预测的准确度.

为了进一步验证上述结论,在此用实验测得的数据(ΔGtr)[10]代替PMD作为响应量,同样分别进行了单参数和双参数的拟合.

单参数fpSA的预测公式(R2=0.36)为:

结果表明,利用双参数拟合也可使R2从0.36提高到0.98,这进一步验证了渗透剂分子体积V和fpSA二次项的引入提高了模型的精度.

2.4 模型自变量对渗透剂稳定能力影响的分析

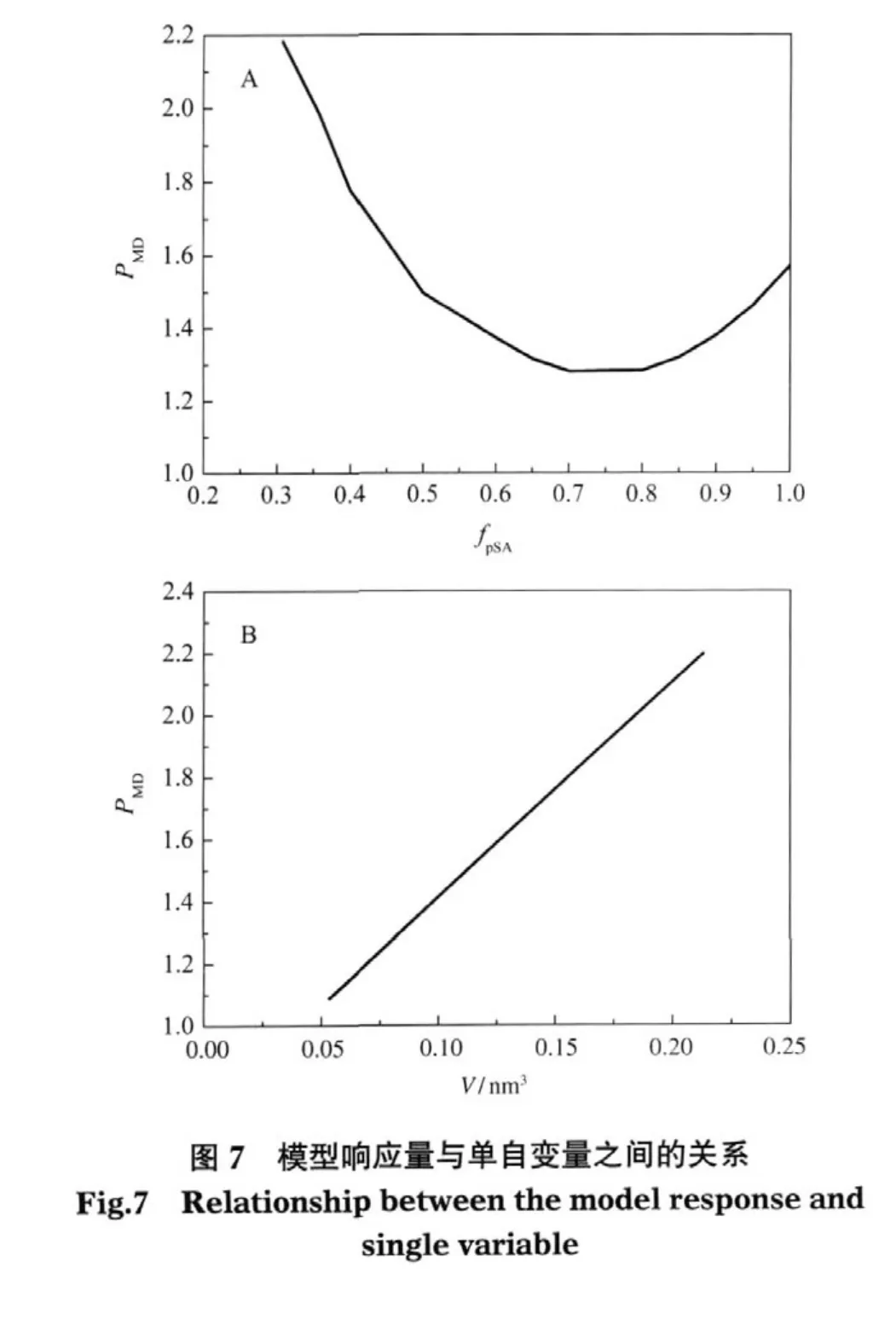
为了进一步分析模型自变量(V,fpSA)对渗透剂稳定能力的影响,将一个自变量固定在其平均值附近,计算得到PMD随另一个自变量的变化趋势(图7).在图7A中,当fpSA的值较小时(fpSA＜0.7),PMD会随着fpSA的上升而下降,这与Bolen等[10]的研究结果一致,即渗透剂的稳定能力与其fpSA负相关.但是,受公式中fpSA二次项的影响,当 fpSA值大于 0.7时,fpSA的增加反而会使渗透剂的稳定能力逐渐增高,即此时渗透剂的稳定能力与fpSA呈正相关.此结果即可用于解释多羟基类渗透剂对蛋白质的稳定能力会随着fpSA的增加而上升的原因.同时也说明fpSA二次项的引入是使模型精度提高的原因之一.

图7B所示为渗透剂的保护能力(PMD)随其体积(V)的变化情况.结果表明,PMD始终随着V的增大而增大.分析原因认为,分子体积代表了渗透剂分子在蛋白质表面空间位阻效应的大小,较大的体积有助于它们被蛋白质优先排阻,而许多研究证明渗透剂的优先排阻作用是其稳定蛋白质的主要作用力.因此渗透剂的稳定能力与其分子体积呈正相关[37-38].

3 结 论

利用分子动力学模拟和统计学分析方法,考察了不同渗透剂对CI2热稳定性的影响,并且将渗透剂的极性表面积分率(fpSA)和分子体积(V)同时作为自变量,并引入fpSA二次项,分别以模拟得到的热稳定能力(PMD)和实验测得的转移自由能(ΔGtr)值为响应量,进行双参数拟合.结果显示:渗透剂会不同程度地提高CI2对热的稳定性;本研究根据分子动力学模拟结果定义并计算得到的一维结构参数能够较好地描述在热变性条件下渗透剂对CI2的稳定能力;渗透剂对蛋白质的热稳定能力与其V成正比,并由于拟合公式中fpSA二次项的引入,fpSA与渗透剂的稳定能力不再仅呈现负相关,当极性表面积分率大于0.7时,其与渗透剂的稳定能力即可呈现正相关.并且渗透剂的V和fpSA二次项的引入可大大提高仅以fpSA为单参数的模型的精度,说明在分析渗透剂对蛋白质的稳定能力时,同时考虑渗透剂V和fpSA即可大大提高模型预测的准确度.另外,当使用ΔGtr作为拟合模型的响应量时,也可得到相似的结论,这从另一个侧面证明了模拟结果与实验结果具有很好的相关性.

1 Yancey,P.H.American Zoologist,2001,41:699

2 Timasheff,S.N.Annu.Rev.Biophys.Biomol.Struct.,1993,22:67

3 Ou,W.B.;Park,Y.D.;Zhou,H.M.Eur.J.Biochem.,2001,268: 5901

4 Arakawa,T.;Timasheff,S.N.Biophys.J.,1985,47:411

5 Ma,L.;Wei,Z.Q.;Huang,A.M.;Yang,H.;He,W.R.;Lin,R.S. ActaChim.Sin.,2009,67:1566 [马 林,魏志强,黄爱民,杨 华,何维仁,林瑞森.化学学报,2009,67:1566]

6 Auton,M.;Bolen,D.W.Methods Enzymol.,2007,428:397

7 Bolen,D.W.;Rose,G.D.Annu.Rev.Biochem.,2008,77:339

8 Bolen,D.W.;Baskakov,I.V.J.Mol.Biol.,2001,310:955

9 Liu,Y.;Bolen,D.W.Biochemistry,1995,34:12884

10 Street,T.O.;Bolen,D.W.;Rose,G.D.Proc.Natl.Acad.Sci.U.S. A.,2006,103:13997

11 Li,S.Q.;Lin,R.S.Acta Phys.-Chim.Sin.,2002,18:825 [李淑芹,林瑞森.物理化学学报,2002,18:825]

12 Zhang,Y.;Ji,B.;Ling,P.;Zhang,T.Eur.J.Pharm.Biopharm., 2007,65:18

13 Li,S.Q.;Sang,W.Q.;Lin,R.S.Acta Phys.-Chim.Sin.,2002,18: 1110 [李淑芹,桑文强,林瑞森.物理化学学报,2002,18:1110]

14 Lerbret,A.;Bordat,P.;Affouard,F.;Hedoux,A.;Guinet,Y.; Descamps,M.J.Phys.Chem.B,2007,111:9410

15 Liu,F.;Ji,L.;Dong,X.Y.;Sun,Y.J.Chem.Phys.,2010,DOI: 10.1063/1.3453713

16 Otzen,D.E.;Itzhaki,L.S.;elMasry,N.F.;Jackson,S.E.;Fersht, A.R.Proc.Natl.Acad.Sci.U.S.A.,1994,91:10422

17 McPhalen,C.A.;Svendsen,I.;Jonassen,I.;James,M.N.Proc. Natl.Acad.Sci.U.S.A.,1985,82:7242

18 Day,R.;Bennion,B.J.;Ham,S.;Daggett,V.J.Mol.Biol.,2002, 322:189

19 Day,R.;Daggett,V.Protein Sci.,2005,14:1242

20 Bennion,B.J.;Daggett,V.Proc.Natl.Acad.Sci.U.S.A.,2003, 100:5142

21 Bennion,B.J.;Daggett,V.Proc.Natl.Acad.Sci.U.S.A.,2004, 101:6433

22 Jackson,S.E.;Fersht,A.R.Biochemistry,1991,30:10428

23 Kundu,S.;Roy,D.J.Mol.Graph.Model.,2008,27:88

24 Duan,Y.;Kollman,P.A.Science,1998,282:740

25 Beck,D.A.;Daggett,V.Biophys.J.,2007,93:3382

26 van Aalten,D.M.;Bywater,R.;Findlay,J.B.;Hendlich,M.; Hooft,R.W.;Vriend,G.J.Comput.Aided Mol.Des.,1996,10: 255

27 Melo,E.P.;Chen,L.;Cabral,J.M.;Fojan,P.;Petersen,S.B. Otzen,D.E.Biochemistry,2003,42:7611

28 Lins,R.D.;Pereira,C.S.;Hunenberger,P.H.Proteins,2004,55: 177

29 Sun,H.;Jiang,Y.J.;Yu,Q.S.;Zou,J.W.Acta Phys.-Chim.Sin., 2009,25:635 [孙 浩,蒋勇军,俞庆森,邹建卫.物理化学学报,2009,25:635]

30 Zhao,Y.S.;Zheng,Q.C.;Zhang,H.X.;Chu,H.Y.;Sun,C.C. Acta Phys.-Chim.Sin.,2009,25:417 [赵勇山,郑清川,张红星,楚慧郢,孙家钟.物理化学学报,2009,25:417]

31 Van der Spoel,D.;Lindahl,E.;Hess,B.;Groenhof,G.;Mark,A. E.;Berendsen,H.J.J.Comput.Chem.,2005,26:1701

32 van Gunsteren,W.F.;Billeter,S.R.;Eising,A.A.;Hünenberger, P.H.;Krüger,P.;Mark,A.E.;Scott,W.R.P.;Tironi,I.G. Biomolecular simulation:the GROMOS96 manual and user guide. Vdf Hochschulverlag AG an der ETH Zürich:Zürich,1996

33 Darden,T.;York,D.;Pedersen,L.J.Chem.Phys.,1993,98: 10089

34 van Gunsteren,W.F.;Berendsen,H.J.C.Mol.Phys.,1977,34: 1311

35 Beredsen,H.J.C.;Postma,J.P.M.;van Gunsteren,W.F.;Di Nola,A.;Haak,J.R.J.Chem.Phys.,1984,81:3684

36 Humphrey,W.;Dalke,A.;Schulten,K.J.Mol.Graph.,1996,14: 33

37 Timasheff,S.N.Biochemistry,1992,31:9857

38 Shimizu,S.;Smith,D.J.J.Chem.Phys.,2004,121:1148

Effects of Molecular Volume and Fractional Polar Surface Area of Osmolytes on the Thermal Stability of Chymotrypsin Inhibitor 2

LIU Fu-Feng JI Luo DONG Xiao-Yan*
(Department of Biochemical Engineering,School of Chemical Engineering and Technology,Tianjin University,Tianjin 300072, P.R.China; Key Laboratory of Systems Bioengineering,Ministry of Education,Tianjin University,Tianjin 300072,P.R.China)

We correlated the protective ability of osmolytes on proteins with their fractional polar surface area(fpSA) and molecular volume(V).Thus,both parameters need to be considered when the protective ability of osmolytes is analyzed.We carried out molecular dynamics simulations of the chymotrypsin inhibitor 2(CI2)in different osmolytes to probe the molecular basis of the stabilizing effect.Based on the simulation data,a one-dimensional structure parameter was first calculated.We then used a statistical bivariate fit model to obtain a theoretical model,which represents the stability capacity of the osmolytes.Finally,the model was used to analyze the correlation between the two parameters(fpSAand V)and the protective ability of the osmolytes.We found that the one-dimensional structure parameter characterized the protective ability of the osmolytes well.Using this model,the protective stability of the osmolytes can be analyzed accurately.The inclusion of V and the two-order term of fpSAgreatly increases the accuracy of the model.The protective capacity of the osmolytes increases with V.In addition,we introduced the two-order term of fpSAinto the fit formula.We found that the fpSAof the osmolytes is negatively correlated with its protective abilitywhen it is less than 0.7.However,when the fpSAof the osmolytes is larger than 0.7,it is positively correlated with its protective ability.

Molecular dynamics simulation; Protein stability; Osmolyte; Fractional polar surface area; Molecular volume

O641

Received:June 28,2010;Revised:July 19,2010;Published on Web:August 27,2010.

*Corresponding author.Email:d_xy@tju.edu.cn;Tel:+86-22-27406590.

The project was supported by the National Natural Science Foundation of China(20636040,20876111,20906068),National Key Basic Research

Program of China(973)(2009CB724705),Natural Science Foundation of Tianjin from Tianjin Municipal Science and Technology Commission,

China(08JCZDJC17100),and Independent Innovation Foundation of Tianjin University,China.

国家自然科学基金(20636040,20876111,20906068),国家重点基础研究发展规划项目(973)(2009CB724705),天津市科委自然科学重点基金(08JCZDJC17100)和天津大学自主创新基金资助

ⒸEditorial office of Acta Physico-Chimica Sinica