Negative permeability in planar metal-dielectric composites

HUANG Zhi-ming,ZHANGDao-hua,HOU Yun,CHU Jun-hao

(1.School of Electrical and Electronic Engineering,N anyang Technological University,Singapore,639798;2.National Laboratory for Infrared Physics,Shanghai Institute of Technical Physics,Chinese Academ y of Sciences,Shanghai200083,China)

1 Introduction

Metamaterials open the door to a variety of new physical phenomena and potential applications[1-4].For example,negative refractive index,in which both the permittivity and per meability are negative,would reverse nearly all known optical phenomena.A negative permittivity is not unusual and occurs in any metal from zero frequency to the plasma frequency.However,a negative per meability at optical frequencies does not occur in naturalmaterials.

Following the proposal of Pendryet al.,magnetic metamaterials have been formed from a periodic array of nonmagnetic,conducting,Split-ring Resonators(SRRs),achieved in essence just by m imicking a s mallLCcircuit structure of eigenfrequencyωLC=(LC)-1/2[2]. Each SRR structure consists of a magnetic coil with inductanceLand a capacitorwith capacitanceC.Since the first demonstration at microwave frequencies[9],the achieved magnetic resonance frequencies have been increased by more than four orders of magnitude over the last few years[5-8]. However,the extension to higher optical frequencies and larger areas faces a great challenge.This is because such metamaterials need the SRRs to have sizes down to about 100 nm and lesswith critical features at the level of～10 nm,and a density of～1010cm-2.This is technologically difficult to achieve. Further more,the inherent losses associated with scaling down make the materials impractical formost applications.

In this article,we report a new metamaterial formed by two thin parallelplates separated by a die-lectric medium,where the top plate is semitransparent to light.The magnetic resonant response at optical frequencies from thismetamaterial is experimentally observed by spectroscopic ellipsometry,and verified by Faraday′sLaw and optical transfermatrix methods.The new structure is of significant importance for applications,especially at optical and terahertz frequencies,because perfect interfaces and/or surfaces can be successfully realized in the layered structures usingmodern growth techniques[9,10].

2 Experiments

We designed and fabricated three samples which consist of three layers-LaNiO3,Pb(ZrTi)O3,and Pt on a Sisubstrate. The opticalsemitransparent LaNiO3layer is on top followed by the Pb(ZrTi)O3and Pt,as shown in Fig.1.The thicknesses of the LaNiO3and Pt are the same for all three samples,namely 45 and 50 nm,respectively,while the thicknesses of the Pb(ZrTi)O3for SamplesⅠ,Ⅱ andⅢare 645,575,and 500 nm,respectively.They were grown by radio frequencymagnetron sputtering.Spectroscopic Ellipsometric(SE)measurementswere carried out using the variable-angle infrared spectroscopic ellipsometer(PhE-104)[11]in the wavelength range of 2.5-12.5μm.The accuracy of the measured tanψ and cosΔ is better than 1%.

Fig.1 Illustration of the three layer unifor m metamaterials.The thicknesses of the top and bottom layers are fixed at 45 and 50 nm,respectively while the thickness of the Pb(ZrTi)O3is 645,575 and 500 nm,respectively,for the three samples.

3 Results and Discussion

Fig.2 shows the value of tanψat different frequencies of Sample I at three different incident angles of 20°,60°and 70°,respectively.An obvious resonant peak is observed around 6.9μm,which indicates that the amplitude of thep-polarized light is much stronger than that of thes-polarized light.The peak shifts slightly and its intensity varies with the angle of the incidence.Beyond this resonant peak,tanψ ＜1 for the three angles of incidence.These are obviously the features of a magnetic response rather than an electric response.

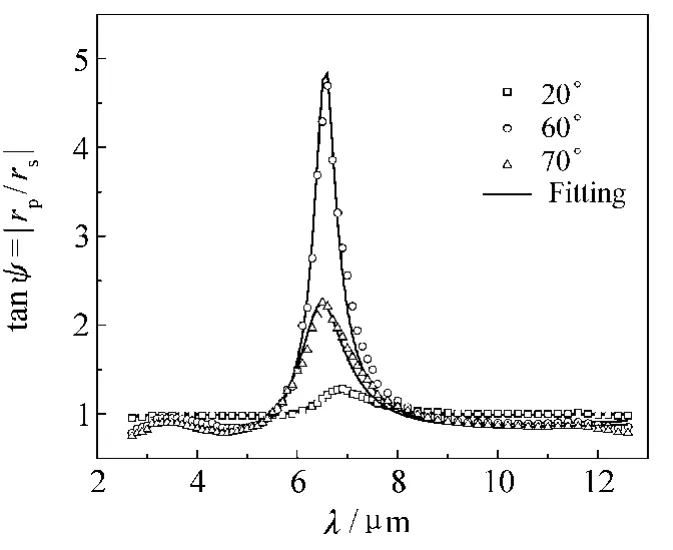
Fig.2 Amplitude ratio tanψof LaNiO3/Pb(ZrTi)O3/Ptmetamaterial(SampleⅠ)measured at three different incident angles 20°(square),60°(circle),and 70°(triangle).

If the magnetic response centred at 6.9μm in the spectrum for SampleⅠresults from the metamaterial,then the resonant frequency should scale with dimensions because of Maxwell equations. In order to verify this observation,two more metamaterials(SamplesⅡandⅢ)with different d imensions are also characterized and the results measured at normal incidence for the three samples are shown in Fig.3.As can be seen from Fig.3,two metamaterials exhibit a s imilar magnetic mode to SampleⅠ,and their resonant frequencies occur at 6.5 and 5.8μm,respectively. These observations clearly indicate that the magnetic response indeed results from the metamaterial structures. In addition,one can also see that the ratios of the resonant frequency over the total thickness of the composite are about 9.30,9.70 and 9.74 for SampleⅠ,Ⅱ andⅢ,respectively.This indicates that the composites are of sub-wavelength order and each of them behaves as an effective medium.

Fig.3 Reflectance ratio of thep-polarization tos-polarization response as a function of wavelength of SampleⅠ(solid),Ⅱ(dash),andⅢ(dott)at an incident angle of 20°.The resonance wavelength shifts to higher energy as the thickness of the medium layer decreases.

From the SE data,the transmission and reflectance infor mation can be extracted and then the metamaterial effective per meabilityμeffcan be estimated using transfer matrix method[12-14]. Fig.4 shows the estimated real(μr)and imaginary(μi)parts of the effective magnetic permeabilities for the three samples.Three features can be seen in this figure: 1)the magnetic resonantresponses are obtained for all three samples with the centre wavelengths the same as those of the corresponding ellipsometric data;2)obvious negative permeabilities are achieved with minima in the negative per meability of about-1.68 at 51.7 THz,-1.47 at 56.6 THz and-125 at 63.8 THz,respectively;3)the negative permeabilities occur at frequencieswhich are at the resonant ones for all three samples,because the induced dipole moments lag and are completely out of phase with the excitation fields.This is an important precondition for the realization of negative index of refraction in a homogeneous layered metamaterial.

Fig.4 Real(μr)and imaginary(μi)parts of the effective magnetic permeability estimated with the transfermatrixmethod for SamplesⅠ,Ⅱ,andⅢ.

To further verify the magnetic response of the metamaterials,we perfor med a numerical simulation using Faraday′s Law. For simplification,we assumed identical impedance for the top and bottom layers.All the remaining parameter values come from the experimental data.The results are shown in Fig.5 for SampleⅠ.Both the shape and peak posi-

Fig.5 Comparison of the real(top)and imaginary(bottom)part of the effective magnetic per meability function for SampleⅠcalculated by the transfer matrixmethod(solid)and Faraday′sLaw method(dash),respectively.

tion coincide well with those estimated from the transfermatrixmethod.The narrowed width and increased height are from Faraday′sLaw mainly due to the substitution of the symmetric top metal plate for the semitransparent conducting film.

4 Conclusions

In conclusion,magnetic resonance and negative permeability in the infrared region have been realized in the homogeneous layered metamaterial consisting of a pair of parallel plates separated by a layer of themedium.The resonant frequency and the value of the negative permeability can be varied by changing the thickness of the composite.Such metamaterials can be easily fabricated with mature thin film technology and are of great significanceto device applications.

[1] VESELAGO V G.The electrodynamics of substance with simultaneously negative value ofεand&μ[J].Sov.Phys.Usp.,1968,10:509-514.

[2] PENDRY J B,HOLDEN A J,ROBB INSD J,et al..Magnetis m from conductors and enhanced nonlinear phenomena[J].IEEE Trans.M icrowave Theory Tech.,1999,47:2075-2084.

[3] PENDRY J B.Negative refraction makes a perfect lens[J].Phys.Rev.Lett.,2000,85:3966-3969.

[4] S M ITH D R.How to build a superlens[J].Science,2005,308:502-503.

[5] YEN T J,PAD ILLA W J,FANGN,et al..Terahertz magnetic response from artificialmaterials[J].Science,2004,303:1494-1496.

[6] L INDEN S,ENKR I CH C,WEGENER M,et al..Magnetic response of metamaterials at 100 terahertz[J].Science,2004,306:1351-1353.

[7] ZHANG S,FAN W,M INHASB K,et al..Midinfrared resonantmagnetic nanostructures exhibiting a negative permeability[J].Phys.Rev.Lett.,2005,94:037402.

[8] ENKR I CH C,WEGENERM,L INDEN S,et al..Magneticmetamaterials at telecommunication and visible frequencies[J].Phys.Rev.Lett.,2005,95:203901.

[9] FONGD D,STEPHENSON GB,STREIFFER S K,et al..Ferroelectricity in ultrathin perovskite films[J].Science,2004,304:1650-1653.

[10] DEHL INGER G,D IEHL L,GENNSER U,et al..Intersubband electroluminescence from silicon-based quantum cascade structures[J].Science,2000,290:2277-2280.

[11] HUANG ZM,CHU J H.Optimizing precision of fixed-polarizer,rotating-polarizer,sample,and fixed-analyzer spectroscopic ellipsometry[J].Appl.Opt.,2000,39:6390-6395.

[12] S M ITH D R,SCHULTZ S,MARKOŠP,et al..Determination of effective per mittivity and per meability of metamaterials from reflection and trans mission coefficients[J].Phys.Rev.B,2002,65(3):195104.

[13] HUANG ZM,XUE J Q,HOU Y,et al..Opticalmagnetic response from parallelplatemetamaterials[J].Phys.Rev.B,2006,74(19):193105.

[14] CHEN X,GRZEGORCZYK TM,WU B,et al..Robustmethod to retrieve the constitutive effective parametersofmetamaterials[J].Phys.Rev.E,2004,70(1):016608.