基于最优小波包基的信号增强算法研究及应用

张花花

（兰州交通大学 电子与信息工程学院 兰州 730070）

0 引言

小波包基的选择对于信号的小波包变换相当重要,它决定着小波包分解的效果。由于小波包基种类繁多,其特性各不相同,对于同一个信号,选择不同的小波包基进行分解,其结果会有所不同。如何选择小波包基对信号进行分解才能得到最佳的分解效果是在小波包分解时首先会遇到的问题，所以我们希望根据不同分析信号的特征来选择一个最好的小波包基，用来表达信号的特点。于是，本文选择目前比较常用的香农熵来作为寻找最优小波包基的代价函数，根据Shannon熵准则的最优小波包基信号去噪算法，并将其应用于带噪语音信号的消噪。该算法在最优小波包基的基础上，对进行小波包分解后的小波包系数进行阈值处理，用量化后的系数重构得到去噪后的信号。通过仿真，我们可以验证该方法具有良好的去噪性能，能够识别信号所包含的频率成分，很好地保留有用信号，从而达到滤波去噪的目的。而且比较仿真结果可见，该方法消噪效果明显优于基于小波变换的去噪算法，具有广泛的应用前景。

1 最优小波包基的选取

1.1 小波变换与小波包变换基本理论

1.1.1 小波函数和小波包函数的定义

为尺度因子，b为平移因子。

1.1.2 小波包的正交性质

正交性质是小波包基最主要的性质，本文中主要从平移正交性质和的正交关系两方面来解释小波包基的正交性质。

1.1.3 小波包的分解与重构

我们知道信号 ()ft的正交小波分解的公式为：

从式（14）和式（15）中可以看出，用Mallat算法完全可以操作小波包分解。对于每一层的小波包分解实际上是把所有上一层的子带都进行了划分，而小波分解只是把低频子带进行了划分。

1.2 最优小波包基的选择

小波库中有很多小波包基，而不同的小波包基一般具有不同的时频局部化能力，反映不同信号的特性，因此，我们希望根据不同分析信号的特征来选择一个最优的小波包基，用来表达信号的特征。

最佳小波包的选择取决于信号本身的性质，信号分解的目的和最佳原则的选择这几个方面。而要刻画系数的性质，首先要定义一个序列的代价函数，然后在小波库的所有小波包基中寻找使代价函数最小的基。代价函数可以定义为任何关于序列的实函数W，但使用最多的是能测得集中度的可加性代价函数W。其中，集中度是指当系数差不多大时W应大，而当系数差别很大时W应小；可加性指如果满足，则称W为一可加性的信息代价函数。

根据上述定义可以定义很多代价函数，目前比较常用的是shannon熵，即定义序列的熵为：

上面我们对最优基做了解释，下面来讨论一下如何选择最优基的方法。

如图1所示，上方的空间为母空间，下方的空间为子空间。在每一个空间都标上了由式（16）求出的代价函数。图中，阴影部分为最后所选择的小波包。如果子空间的代价总和大于母空间的代价，这说明这一分解是值得的，因此，该子空间应予以保留。反之，若子空间的代价总和大于母空间的代价，则这一分解是不合适的，应放弃，即保留母空间。

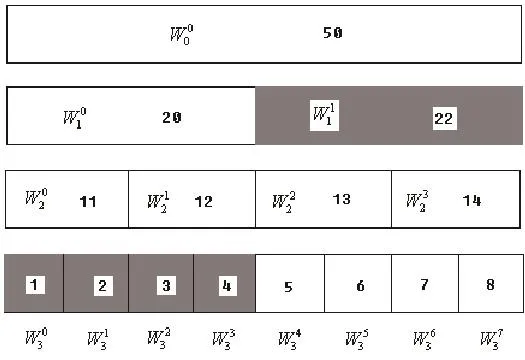
图 1 最优小波包选择

2 基于最优小波包的信号阈值去噪算法

2.1 选择合适的阈值

要达到好的降噪效果，除了选择最优的小波包基函数以外，选择一个合适的阈值也是很关键的，若阈值太小，就无法将噪声完全剔除；相反地，若阈值太大，有用信号将被滤掉，引起偏差。由于小波包分解系数在不同频带反映信号的不同特征，很难找到一个特别有效的统一的阈值算法对各个频带进行处理，因此本文对于小波包分解在不同频带上的系数采用不同的阈值选择算法。

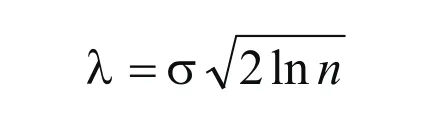
而对于信号突变的部位就采用rigrsure阈值: 该阈值即是利用Stein 的无偏估计求出的SURE阈值，其具体算法如下：

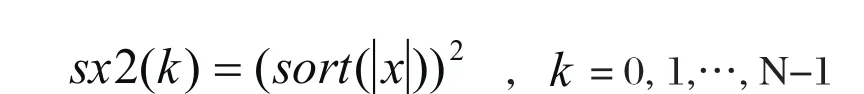
式中，sort是MATLAB中的排序命令。

(2)若取域值为 )(2ksx的第k个元素的平方根，即：

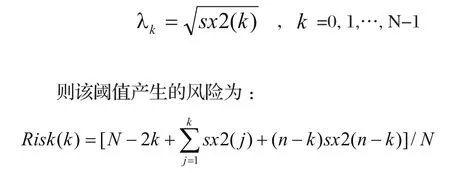
(3)根据所得到的风险曲线 )(kRisk，记其最小风险点所对应的值为mink，那么rigrsure阈值定义为 ：

2.2 基于最优小波包的信号去噪算法具体步骤

（1）根据给定的Shannon熵标准和选择方法，选择适合带降噪信号的最优小波包基；

（2）对信号进行小波包分解时，先确定所需分解的层次N，然后对含噪信号进行N层小波包分解；

（3）对分解后的各个频段根据不同的阈值选择方法选择阈值，对最优小波包基每个节点上的分解系数进行阈值量化，阈值量化采用软阈值方法；

（4）利用经过阈值量化后的小波包基系数进行信号的重构，所得到的信号就是经过最优小波包基去噪后的信号。

3 实验结果分析

以leleccum信号为例，首先根据小波包分解重构原理，通过实例来演示一下利用MATLAB来对小波包进行重构，程序运行仿真图如2所示。

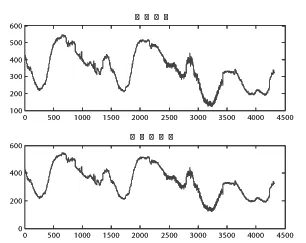
图2 小波包分解重构

采用基于最优小波包基的阈值降噪算法对加了随机噪声的leleccum信号进行降噪处理，同时为了对比小波包降噪与小波降噪，对含随机噪声的leleccum信号也进行了小波降噪，其仿真图如3所示。

图3 小波包降噪与小波降噪仿真图

仔细观察上图可以看出，对比c仿真图和d仿真图，在0到500区间段与2500到3000区间段内，在采用相同的小波母函数、分解层数和阈值选取方法的情况下有明显的差异，基于最优小波包基信号去噪算法效果明显优于基于小波变换的去噪算法，具有更精细的信噪分离能力。

4 结论

本文深入研究了基于最优小波包基的信号降噪噪算法，通过利用MATLAB仿真来验证对加噪的leleccum信号进行基于最优小波包和小波的信号消噪。该算法在最优小波包基的基础上，利用sym6对含噪信号进行了5层分解后再对其进行阈值量化，用量化后的系数重构得到去噪后的信号。仿真结果表明，该方法具有良好的去噪性能，能够识别和确定信号所包含的频率成分，根据Shannon熵准则选择一个最优的小波包基来滤除信号的周期分量和噪声，保留了所需的信号，达到了滤波去噪的目的。并且由仿真结果比较可见，该方法消噪效果明显优于基于小波变换的去噪算法，将具有更为广泛的应用前景。

[1] DONG Y S,YIXM． Wavelet denosing based on four improved function for threshold estimation[J]． Journal of Math, 2006, 26(5): 473-477．

[2] Lei Zhang, Paul Bao ．Denoising by Spatial Correlation Thresholding[J]． IEEE Transations on Circuits and System for Video Technology 2003:13(6):535-538．

[3] 葛哲学，沙威，小波分析理论与MATLAB R2007实现[M]．北京：电子工业出版社，2007．

[4] 孙延奎，小波分析及其应用[M]．北京：机械工业出版社，2005．

[5] Ingrid Daubechies，小波十讲[M]．李建平，杨万年译．北京：国防工业出版社，2004．

[6] 董长虹，高志，余啸海，Matlab小波分析工具箱原理与应用[M]．北京：国防工业出版社，2004．

[7] 王维, 张英堂, 任国全,小波阈值降噪算法中最优分解层数的自适应确定及仿真[J]．仪器仪表学报，2009．

[8] 臧先峰,张正道, 基于小波熵的最优阈值去噪方法 [J]．江南大学学报，2009．

[9] 史贤俊, 林飒, 李瑞亮, 基于最优小波包基的信号去噪算法及其应用[J]．海军航空工程学院学报， 2006．