基于结构可靠度的在役桥梁剩余价值分析研究

陈 莘

(安徽省公路桥梁工程公司,安徽合肥 230031)

基于结构可靠度的在役桥梁剩余价值分析研究

陈 莘

(安徽省公路桥梁工程公司,安徽合肥 230031)

对在役桥梁进行剩余价值分析,对于路政部门加强桥梁维护维修、加固甚至新建等决策管理都有实际意义。基于可靠度理论提出了一种折旧方法并用其进行剩余价值计算,为公共项目建设宏观经济的成本分析提供一种量化的工具。

桥梁工程;维护维修与加固;管理

0 引言

在进行桥梁改造升级与新建桥梁之间的方案比选和经济决策时,需要考虑现有的在役桥梁的剩余价值问题,此时,用会计学方法来做宏观经济分析显然不合适[1]。在役桥梁实际运营过程中,由于各种因素的影响,桥梁的使用寿命存在不确定性,本文试图提出基于桥梁可靠度的方法来探讨在役桥梁的剩余价值。

安全性、适用性和耐久性总称为结构的可靠度。目前,国际上对结构可靠度的一致定义为:结构在规定的时间内,在规定的条件下,完成预定功能的概率[2]。结构可靠度的提出就是为了使结构在安全适用和经济合理之间选择一种合理的平衡,本身就是一种基于技术可行性和经济合理性的产物,是技术和经济结合的一个指标。大连理工大学的赵国藩等人在旧有结构性能评估[3]和结构全过程可靠度[4]研究中取得了大量成果,从而使我们在判定在役桥梁的结构状态时有了相应依据。根据当时状态而判断其剩余价值,在理论上和操作上应该具有相当的可行性。

1 在役桥梁资产折旧计算参数的确定

1.1 折旧的基数

计算固定资产折旧的基数一般为取得固定资产的原始成本,即固定资产的账面原值。本文所讨论的在役桥梁账面原值指的是从立项、设计、施工阶段构成固定资产的资金投入。

1.2 固定资产的净残值

固定资产的净残值是指预计的固定资产报废时可以收回的残余价值扣除预计清理费用后的数额。和其他一般的固定资产不同,桥梁工程到了使用末期可能存在负的净残值,即为数不菲的拆桥费用。

1.3 固定资产的使用年限

固定资产的使用年限是指固定资产预计的经济使用年限。在确定固定资产使用年限时,不仅要考虑固定资产的有形损耗,还要考虑固定资产的无形损耗。我国目前处在经济大发展时期,交通基础措施的建设处于滞后阶段,一般可以认为在役桥梁的经济寿命为其自然寿命。

2 基于结构可靠度的在役桥梁剩余价值分析方法

2.1 桥梁的可靠度理论模型

一般认为结构的恒载效应服从正态分布,其统计参数可以通过实测得到。己有结构的可变荷载效应是一个与剩余使用寿命期有关的量,可以根据结构在已服役期内的荷载实测资料进行统计分析。如果没有足够的实测资料,可以按设计时荷载的统计特性进行推算。结构上的可变荷载效应服从极值I型分布,时段t内可变荷载效应的平均值μSQt,标准差σSQt可以表示为:式中:TS为规范给定的结构设计使用期;μSQT和σSQT分别为设计使用期内荷载效应极大值的平均值和标准差。

己有结构是一个客观存在的实体,其抗力理论上可视为一确定量,但是由于各种因素的影响以及检测手段的限制,测量时存在一定的误差,因此仍具有一定的随机性,抗力随时间变化的模型可以用一个简单的随机过程模型表示为:

式中:R(t)为结构在t时刻的抗力;F(t)为结构抗力衰减—时间函数(与结构的组成材料、环境以及维护条件有关)。

第ti时刻的功能函数为:

式中:R(ti)为结构ti时刻结构抗力;SQ(ti)为ti时刻可变荷载效应;SG为恒载效应。在时段[0,t]内结构的失效概率可以表示为:

相应的可靠指标为:

βi为[0,t]时段内的可靠指标;Φ-1(·)为正态分布函数的逆函数。

2.2 基于可靠度的在役桥梁剩余价值

一般的折旧方法,以平均年限法为例,固定资产在某一时刻的剩余价值计算公式如下:

年折旧率=[(1一预计净残值率)/折旧年限]×100%

年折旧额=固定资产账面原值×年折旧率固定资产剩余价值=固定资产账面原值—∑年折旧额

根据这种思路,考虑以结构的失效概率作为其折旧率,其可靠度为目前的剩余价值比率,那么,对处在ti时刻的在役桥梁,其剩余价值计算流程为:

(1)对在役桥梁的性能进行评估,得到当前状态的可靠度指标。

(2)用可靠度指标与经济参数相乘,得到在役桥梁的剩余价值。

式中:Vsi为当前桥梁的剩余价值;βti为当前状态的可靠度指标;V0为桥梁折旧的计算基数,即桥梁的初始价值;Cb为桥梁拆除的花费(净值)。

3 在役桥梁剩余价值计算方法的修正

式(8)有一个明显的问题,就是没有考虑资金的时间价值。要考虑资金运动中的增值,就必须对该公式进行修正。

3.1 理论上的在役桥梁剩余价值的计算公式

在考虑资金时间价值的情况下,理论上的在役桥梁剩余价值的计算公式为:

式中:dPf(t)为失效概率的增量微元;Pt为t时刻的资金折现系数;Pb为拆除时的资金折现系数。

对于式(9),dPt(t)与Pt的确定是比较难的。但可通过离散的方法将之转化解决。

3.2 离散化的解决办法

文献[4]中将设计基准期分成m个相等的时段,将荷载随机过程离散成m个随机变量SQ(ti),将抗力随机过程离散成m个随机变量R(ti),R(ti)的大小取第i个时段抗力的中值,推导出了考虑抗力变化的结构可靠度的实用计算方法,同时指出,若可变荷载的极大值分布服从极值I型分布时,结构在[0,t]时段内的失效概率为:

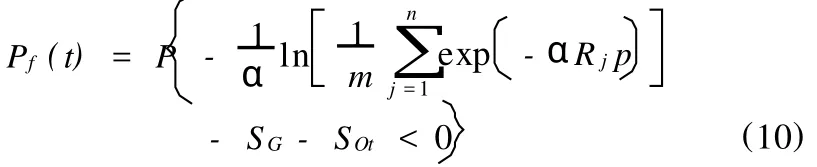
式中:α为极值I分布的参数;m为将[0,t]分隔成的时段数;Rj为第j个时段结构抗力效应的中值;SQt为[0,t]时段内可变荷载效应的极大值。

可将R视为结构的等效抗力,反应的是结构抗力的退化过程。

结构在某一时段[ti,ti+δt]内的失效概率增加量为:

对于某一个确定的时间点,资金的折现系数也容易根据相关表格得到。那么此时的计算公式应该为: 3.3 离散化处理后桥梁剩余价值计算流程

计算结构某一时段的在役桥梁剩余价值的计算步骤如下:

(1)描述结构所处的环境及材料特性,建立结构抗力衰减模型。

(2)实测当前状态下结构抗力和荷载的统计参数。

(3)把设计基准期离散化,根据式(6)计算各个时段的失效概率Pfi(t)。

(4)根据公式(12)计算各个时段的失效概率增加量Pfi。

(5)根据折现系数表和相应的参数(折现率、时段长)查出折现各Pfi(t)时对应的Pi。

(6)根据式(13)计算现阶段桥梁剩余价值Vsi。

4 算例分析

某大桥位于国道101线,桥梁上部构造为装配式钢筋砼无中横隔梁T形梁桥,混凝土标号为C25,内梁采用火山灰水泥,外梁采用普通水泥。下部为双柱墩,基础有2种型式:钻孔桩基础与浅基础。利用实际检测数据建立钢筋锈蚀和混凝土强度时变模型,对钢筋混凝土梁桥抗弯承载力进行计算,得出如图1所示的抗力时变规律。

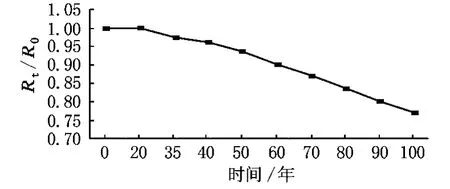
图1 抗力时变规律曲线

图中:R0为桥梁结构构件服役时间t=0时的抗力均值;Rt为桥梁结构构件服役时间为t时的抗力均值。

由图1可见:桥梁结构抗力在服役期内不断衰减,衰减速度并不均匀,初期较慢,后期较快。在服役前20年内该桥的结构抗力衰减速率为0,在后期衰减速率逐步增加。

该桥投资为28 000万元,设计寿命为100年,拆除后价值为1 500万元,折现率取10%。以建成时间为基期,取40年为计算周期,采用会计学的折旧模式,考虑折旧期间为30年,那么在桥龄为40年时,这部分资产已经提取完折旧,账面残值为0。采用基于结构可靠度的桥梁剩余价值折旧的方法,根据式(13),此时的桥梁价值为:

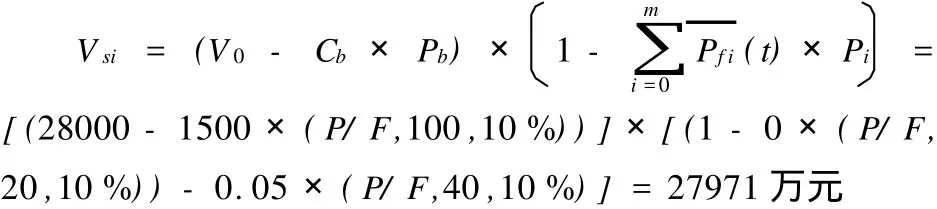
5 结语

在公共项目的评价中,经常采用的是费用收益-成本分析方法。该方法用收益-成本比率作为评价标准。一般说来,人们更关注这些公共设施给公众带来的收益,并建立了各种模型进行分析、预测和评价,对于成本的探讨相对较少。其实公共项目的投资也要讲究其投资效用比,特别是互斥方案的比选,找到比较科学的方法计算其成本更为重要。对于在路网中发挥咽喉作用的桥梁工程,利用相应的方法计算出残余价值对运营法人转交路政部门后的桥梁管理和评价有非常重要的意义,同时,它也是进行旧桥加固和新建桥梁方案比选决策的重要依据。

[1] 邓平.对基础设施固定资产折旧方法的探讨[J].海南大学学报:社会科学版,1999(2):59261.

[2] 张建仁,刘扬,许福友,等.结构可靠度理论及其在桥梁工程中的应用[M].北京:人民交通出版社.2003.

[3] 赵国藩,李云贵.旧有结构性能评估[J].大连理工大学学报,199l(6):687-692.

[4] 赵国藩.贡金鑫.赵尚传.等.工程结构生命全过程可靠度研究[M].北京:中国铁道出版社,2001.

责任编辑:文 月

U44211

A

167128275(2010)052012422.5

2010202224

陈莘(19702),男,安徽合肥人,安徽省公路桥梁工程公司高级工程师。研究方向:路桥工程技术。