土体的并联理想弹塑性弹簧损伤模型

肖红宇,黄 英

(1.湖南省水利水电勘测设计研究总院,湖南长沙 410007;2.昆明理工大学电力工程学院,云南昆明 650051)

土体的并联理想弹塑性弹簧损伤模型

肖红宇1,黄 英2

(1.湖南省水利水电勘测设计研究总院,湖南长沙 410007;2.昆明理工大学电力工程学院,云南昆明 650051)

通过土颗粒之间的连接其在土体受力过程中的变形特性,根据弹塑性理论建立土体的并联弹簧模型。结合土体在受力过程中处于塑性流动的连接数目和土体中连接总数目的比值来建立土体的损伤变量,进而推导出土体受力时的应力应变关系。实例表明,所推导的土体本构关系是合理的。

本构关系;损伤变量;加载;卸载

0 引言

材料的本构关系是反映材料力学性质的数学表达式,岩土材料是一个复杂的系统,因此其力学性状相当复杂,不仅是因为土体的组成相当复杂,而且影响因素很多,如温度、湿度、时间等[1]都对其有很大的影响。从1773年库仑(coulomb)提出土质破坏条件(后来推广为莫尔—库仑准则)以来,各国学者纷纷提出许多岩土的材料的破坏准则[2],每种破坏准则都有一定的适用范围,但没有一种可以通用的破坏准则。在现代的岩土的本构关系中,提出屈服面、塑性势、内变量等概念,都是以晶体滑移为依据的,并不一定符合土体的微观变形机理,现在的岩土力学的研究应该从微观和宏观相结合的道路上进行,在搞清岩土材料的微观变形机理的基础上进行[3]。

损伤力学力学是从1958年前苏联学者Kachanov在金属儒变的研究中提出的,主要说明材料在外部作用下,材料将形成大量的微观裂纹,这些微观缺陷通过形核、扩展、汇合造成材料劣化直到破坏[4]。经过几十年的发展,损伤力学已经发展到适用阶段。中国学者沈珠江在1988年把损伤力学引入土力学[5],随后何开胜[6],赵锡宏[7]等在这方面作了研究。本文从土颗粒微观结构入手,通过谈塑性模型建立了土体的并联弹簧模型,从而建立土体受力时的损伤变量来探讨土体的本构关系,在土体力学性质研究中具有一定的理论价值。

1 模型的建立

1.1 模型假设

土体是由土颗粒通过颗粒之间的连接组成的多孔材料,土体在受力过程中,土颗粒之间的连接要发生变形,一方面土颗粒之间的连接发生弹性变形,当应力撤消以后,土颗粒又回到其原来的位置,另一方面,土颗粒之间的连接发生不可以恢复的塑性变形,土颗粒在土体中的相对位置发生改变,这样土体产生了塑性变形。由于土体中颗粒的变形一般较小,相对土体的变形而言,其变形可以忽略不计,因此土颗粒之间的连接的力学性质直接决定了土体的力学性质。为研究的方便,对土体颗粒之间的连接做如下假设。

人们经常有多种元件来描述材料的特性,常用的有弹簧、滑片、粘壶。沈珠江老先生在研究土体损伤力学的时候提出了胶结杆元件用来描述土体的脆性损伤特性[8],本文将通过理想弹塑性弹簧元件来建立土体的弹塑性模型,为研究方便,对此模型做如下假设:

(1)土体可以看作由N0个弹性系数相同的弹簧并联组成的系统,如图1,N0是一个很大的数目,每一个弹簧的弹性系数为e,且有土体在初始状态时弹性模量为E0=N0e;

(2)每一个弹簧是理想弹塑性体,当某一弹簧应变超过其极限应变值时,弹簧发生塑性流动,且其拉伸极限应变和压缩极限应变绝对值相等,如图2;

(3)每个弹簧的极限应变值不相等,某一应变ε下发生塑性流动弹簧的数目服从平均分布,其分布密度函数为f(ε)=1/εmax,其中εmax为所有弹簧中最大的极限应变值,也就是土体的极限应变值。

图1 土体并联弹簧模型Fig.1 The parallel springsmodel of soilmass

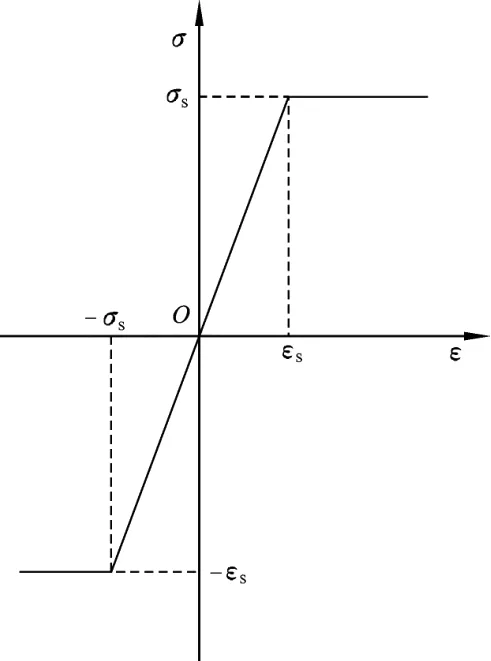
图2 理想弹塑性模型Fig.2 The ideal elastic-plastic model

1.2 土体的本构关系

1.2.1 损伤理论

损伤力学认为,材料的破坏过程是材料中微裂慢慢演化过程,同时也是一个从完全未破坏到完全破坏的过程,描述这一变化过程的关系的参量用损伤变量D来表示,当材料处于完全未破坏状态时,D=0,当材料处于完全破坏状态时,D=1。由损伤变量定义可以知道,材料在某一状态下力学特征可以表示为[9]:

式中:S0表示在完全未损伤状态下材料的某一力学特征参数值;Sd表示完全损伤状态下某一力学特征参数值。损伤变量的确定有多种方法,由以上的弹塑性假设可知,土体在某一应变状态下时,部分弹簧发生了塑性流动,当外荷载增加时,这部分弹簧不再承受所增加的应力。这样,我们可以定义损伤变量为处于塑性流动状态弹簧的数目和土体中总弹簧的数目的比值,即有:

N(ε)为土体处于塑性流动的连接的数量,这样只要可以确定某一应力状态下处于塑性流动状态的弹簧数目就可以确定土体的损伤变量值。

1.2.2 损伤状态下土体的本构关系

沈珠江老先生最先把损伤力学引入土力学,认为土体的破坏也是一个从完全未破坏的到完全破坏的过程。故和金属材料一样,土体的力学特征参量值也是随损伤变量演化而变化的,同样具有如式①的关系。在研究土体弹性模量时,由模型假设2可以知道,土体处于完全破坏状态下时不再承受增加的应力,即完全损伤状态下土体的弹性模量Ed为0,故在某一损伤状态下土体的弹性模量具有如下关系:

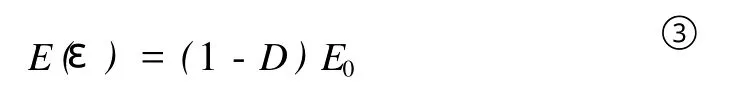
式中:E(ε)为某一应力状态下土体的弹性模量;E0为完全未破坏的状态下土体的弹性模量。

这样土体的应力应变增量关系可以表示为:

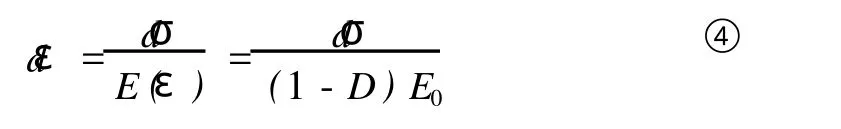
由于土体受力过程是一个损伤演变的过程,我们认为土体在固结完成未加载的时候的弹性模量为土体完全未破坏状态下的弹性模量,即认为土体加载时的初始弹性模量为土体完全未损伤状态下的弹性模量。

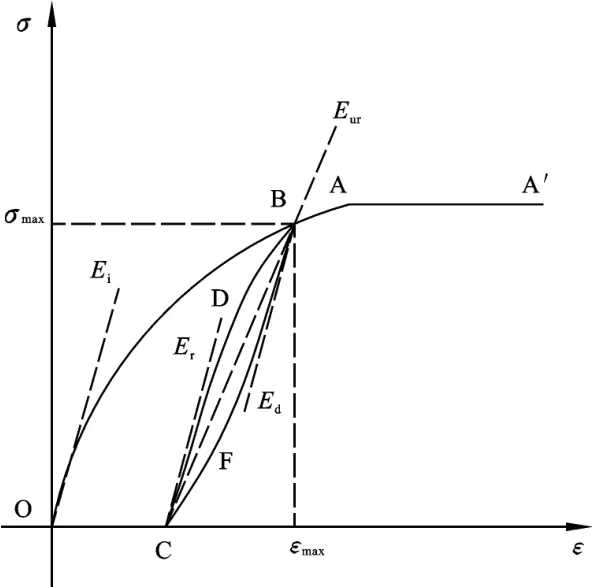
图3 土体加卸载示意图Fig.3 The schematic diagram of soilmass on load and unload

1.2.3 土体加载时的本构关系

土体在加载过程中,如图3中OA段,当加载到某一应变状态ε(ε<εmax)下,极限应变小于ε的弹簧都处于塑性流动的状态,由模型假设条件3,可以知道,此时处于塑性流动的弹簧数量为εf(ε)N0,这样由式②可以建立土体加载的损伤变量为:

其中:D1为土体加载过程中的损伤变量;εmax为土体的极限应变值。由此可以看出,土体在加载的过程中某一状态下,其损伤变量实际可以用该状态下的应变值和土体的极限应变值的比值来决定,这样只要已知土体的某一状态应变值和土体的极限应变值就可以确定土体的损伤变量。

将式⑤代入式④可以得到极限应变范围内土体加载时的应力应变增量关系式为:

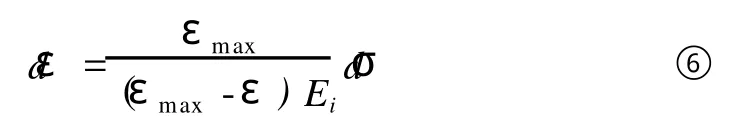
对上式积分整理可得:

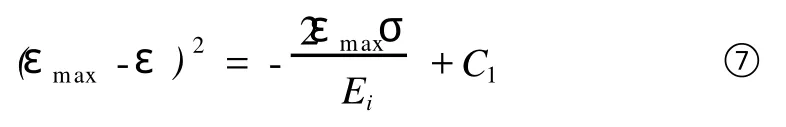
其中C1为积分常数,初始加载条件:σ=0,ε=0,把其代入上式可以得到积分常数C1=εmax2。

由于ε<εmax,则对式⑦两边开方,整理可得极限应变范围内土体加载时的应力应变关系表达式为:

当土体应变达到土体的极限应变时,则所有弹簧都发生塑性流动,即此时土体的应变趋向于无穷,而土体的应力值保持不变,设此时土体所受的应力值为σmax,由式⑧可以解得综合式⑧,可以得到加载时土体的本构关系:

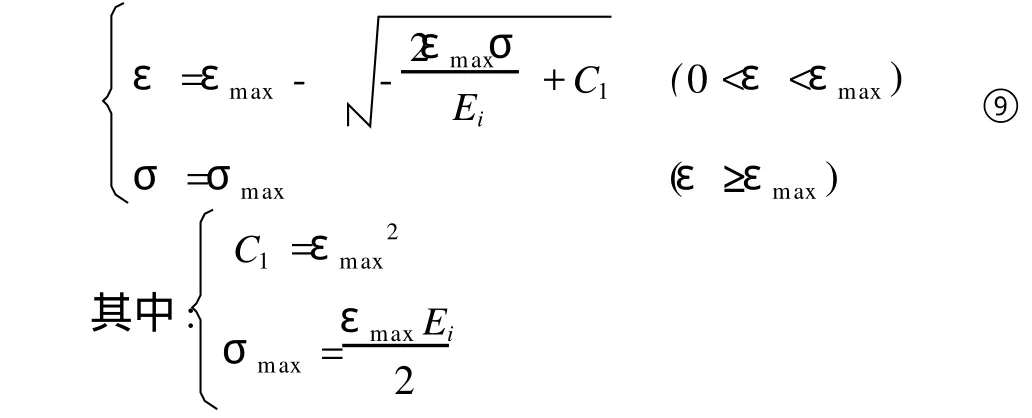
有式⑨可以知,只要确定土体的最大应变值和土体的初始弹性模量,就可以确定土体的加载关系。

1.2.4 土体卸载时的本构关系

设土体在某一应变状态ε1下卸载(如图3中曲线BFC,B点为卸载点),当处于某一应力状态ε时,其卸载应变为Δ ε=ε-ε1,此时部分弹簧由于卸载应变超过了其负应变方向的应变极限而发生反方向塑性流动。由假设3可知,此时处于塑性流动的弹簧数目由于在卸载过程中,0<ε<ε1,所以有|Δ ε|=ε1-ε,这样由式②可以确定土体卸载时的损伤变量为:

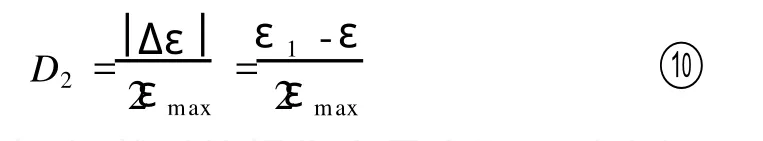
由此可以看出,卸载时的损伤变量实际可以由卸载应变值的1/2和最大应变值之间的比值来确定,这样只要确定了卸载时的初始应变值和土体的极限应变值,则可以确定卸载时某一应变状态下的损伤变量值。

由模型假设2可知土体在卸载时初始弹性模量和土体加载时初试弹性模量相等,故卸载时的初始弹性模量也为Ei,把式⑨代入式④就可以得到土体加载时的应力应变增量关系为:

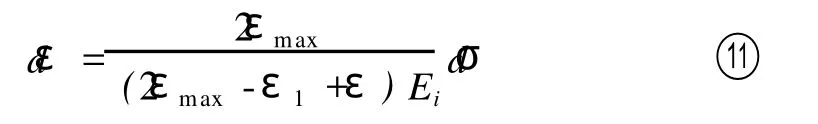
对上式积分可以得到:

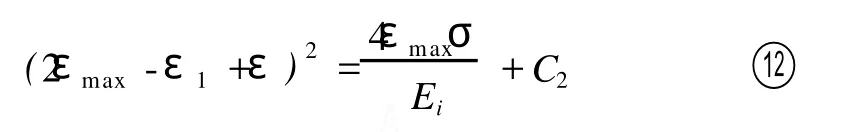
C2为积分常数,设卸载点ε1所对应的应力值为σ1,则卸载的初始条件为σ=σ1,ε=ε1,将其代入式 ⑫可以得到积分常数C2:

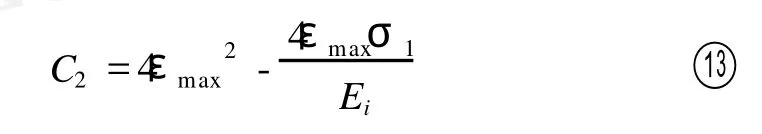
同时由式⑦可以得到在卸载时ε1对应的应力值为:

把σ1和C1代入式 ⑬就可以得到:

对式 ⑫变形,把C2代入可以得到土体卸载时的应力应变关系:

由上式可知当应力值为0时,此关系曲线在σ-ε坐标系中与ε轴的交点值为,即土体的塑性变形值:

土体在卸载完成时,土体的应变并不等于0,即土体发生了不可恢复的变形ε0。由土体的弹塑性理论可知,土体的并不是理想的弹性体,由以上的计算结论可知,在卸载时,可以认为ε0为土体加载过程中产生的塑性变形。

1.2.5 再加载本构关系

土体卸载后对其重新加载时,如图3中CDB段,在没有超过卸载时最大应变时,即ε<ε1时,在卸载时没有发生塑性流动的弹簧在重新加载时同样处在弹性范围之内,不会发生塑性流动;而卸载时在负应变方向发生塑性流动的弹簧在再加载的过程中同样发生正应变方向塑性流动,同样由假设3可知,土体中在应变ε状态下,发生塑性流动的弹簧数目为这样由式②可以得到土体在再加载时的损伤变量:

其中D3为再加载时土体的损伤变量。此时的损伤变量实际上是土体在再加载时应变值的1/2和土体的极限应变值之间的比值,这样只要确定了再加载时初始状态时的应变值和土体的极限应变值,就可以确定某一应变状态下土体的损伤变量。

同理,由假设3可知,在再加载时土体的初始弹性模量也和土体加载时的弹性模量相等,同样也为E0,这样通过式④可以得到土体再加载时的应力应变增量关系:

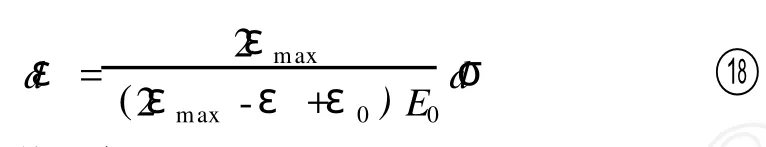
对上式积分可得:

C3为积分常数,由式 ⑲和再加载时的初始边界条件σ=0,ε=ε0,可以得到:C3=4εmax2。

对式 ⑲变形可以得到再加载时应力应变的关系为:

当应变值超过卸载时的最大应变时,应力应变将具有和加载同样的关系,结合式 ⑮、⑨,这样可以得到土体的再加载时的应力应变关系为:

2 实例验证

本文引用文献[1]的实验数据进行验证可以得到,土体的初始弹性模量可以通过某一实测值代如式⑦得到,由实验资料数据代入式⑦,可以得到本土体的初始弹性模量为23.7 MPa;土体的最大应变取土体实测曲线接近塑性流动时的实验值,由实验资料可以取土破坏是最大应变为2.471%,本文采用的卸载应变为1.5%,这样可以得到理论曲线和实验曲线关系如图4。

图4 应力应变关系图Fig.4 The graph of stress-strain relation

由图可以看出,预测曲线和实验曲线相差很小,基本上可以反映土体的本构关系。同时土体卸载和回弹曲线组成回滞环,这和岩土的实验加卸载特性是一致的,同时土体在回弹和重新加载时弹性模量和初始弹性模量接近。

3 结论

(1)土体在加卸载表现弹塑性性质可以看作有由许多理想弹塑性弹簧共同作用的结果,通过理想弹塑性弹簧建立土体弹塑性损伤模型基本上可以反映土体加卸载时的本构关系;

(2)由本文土体模型反映土体的回弹和再加载时组成一个闭和环,可以反映土体在加卸载时产生回滞环的特性;

(3)在加载过程中,土体的弹性模量随着土体的应变的增加而减小,当达到一定的应变时,土体的弹性模量将趋向于0;

(4)土体中连接并不一定服从平均分布,以后的研究可以从找出土体最适应的分布形式,从而建立更加合适土体变形特性的本构关系。

[1] 李广信.高等土力学[M].北京:清华大学出版社,2004.

[2] 郑颖人,沈珠江,龚晓南.岩土塑性力学原理[M].北京:中国建筑工业出版社,2002.

[3] 沈珠江.砂土本构理论的检讨和重建[M]∥第六界全国岩土力学数值分析与解析方法讨论会论文集.广州:广东科学技术出版社,1998.

[4] 余寿文,冯西桥.损伤力学[M].北京:清华大学出版社,1996.

[5] 沈珠江,章为民.损伤力学在土力学中的应用[M]∥第三届全国岩土力学数值分析与解析方法讨论会论文集.武汉:武汉测绘科技大学出版社,1988.

[6] 何开胜.结构性粘土的微观变形机理和弹粘塑损伤模型研究[D].南京:南京水利科学研究院,2001.

[7] 赵锡宏,孙红,罗冠威.损伤土力学[M].上海:同济大学出版社,2000.

[8] 沈珠江.土体变形特性的损伤力学模拟[M]∥第五届岩土力学数值分析与解析方法讨论会论文集.武汉:武汉测绘科技大学出版社,1994.

[9] 沈珠江.结构性粘土的弹塑性损伤模型[J].岩土工程学报,1993,15(3):21-28.

(责任编辑:胡立智)

Parallel Ideal Elastic-plastic Spring Damage Model of SoilMass

XIAO Hongyu1,HUANG Ying2
(1.Hunan Province Hydraulic and PowerDesign Institute,Changsha,Hunan410007;2.Kunm ing University of Science and Technology,School of Electric Power Engineering,Kunm ing,Yunnan650051)

Based on the defor mation property in the process of soil mass in stress because soils was closed with each other,and the elastic-plastic theory,this paper established the parallel spring model of soil mass.And also built up the damage variable of soil based on the ratio be tween the connection number in flexible flow and the total connection number when soilmasswas in stress,then deduced the stress-strain relation of the soilmass in stress.The instance indicated that the stress-strain relation of soilmass deduced in the paperwas appropriate.

constitutive relation;damage variable;load;unload

TU43

A

1671-1211(2010)05-0566-05

2010-07-15;改回日期:2010-09-06

国家自然科学基金资助项目,项目编号:50868009。

肖红宇(1979-),男,工程师,勘察技术与工程专业,从事岩土工程勘察、岩土工程设计等方面的工作。E-mail:xhongyy@126.com