拓扑优化均匀化方法的改进迭代算法
孙 蓓,苏 超
(河海大学水利水电工程学院,江苏南京 210098)
拓扑优化方法是目前结构优化领域研究的热点[1-5].均匀化方法[6]是连续体拓扑优化方法中最常见的一种方法,该方法的一般迭代算法对所有连续体结构都是可用的.若材料特性和荷载情况较为简单,结构规模较小,该方法迭代步较少,计算时间也较短,是一个极为有效的方法,但当结构规模较大,尤其是一些复杂的空间结构(如拱坝),其材料特性和荷载都会出现较为复杂的情况,计算量变大,单步的迭代时间会明显增加,迭代步数也会增多,总计算负荷会很大.为了减少计算时间,提高计算效率和精度,本文对结构拓扑优化均匀化方法的一般迭代算法进行了改进,并引入了用于控制计算过程的2个密度阈值.
1 改进迭代算法的原理
结构拓扑优化均匀化方法[7]在采用有限元方法对设计区域进行离散化[8-9]的基础上,将整个设计空间假设成类似“气孔分布”的微结构单元(单胞),单胞在优化开始前分布均匀,大小相同.在拓扑优化过程中,单胞密度分布发生变化,即高应力区域单胞密度变大,低应力区域单胞密度变小.优化过程中形成了一种承重结构,这种结构在高应力区域气孔“密集”,在低应力区域气孔密度较低[10].当迭代计算全部完成后,再定义一个合理的密度最小值,然后剔除设计空间中单胞密度低于这个最小值的区域,将产生一个材料效应最高的重量优化承重结构[11].
以弹性板壳结构为例,根据有限单元基本理论,可得弹性板壳单元的刚度矩阵

其中
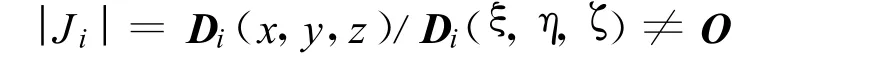
式中:ki——单元刚度矩阵;Bi——单元转换矩阵;Di——单元常量矩阵;ξ,η,ζ——形函数变量;Di(x,y,z)——整体坐标系下单元常量矩阵;Di(ξ,η,ζ)——单元局部坐标系下单元常量矩阵.
采用一般迭代算法时材料密度的求解公式为

其中

式中:ηi——第i个微结构单元密度;W——初始结构材料质量;W*——删除单元的总质量;m——空洞单元数量;ui——单元节点位移矩阵;vi——单元体积;S——迭代步数;vj——空洞单元体积;ε——极小量;C——常量.
对任何迭代计算过程来说,当某一计算数值足够小时,计算机将视其为0,因此引入一个极小量ε,将空洞用密度为ε的单元来替代.材料体积约束(或质量约束)计算时不包括这部分单元的体积(或质量).采用一般迭代算法对结构进行拓扑优化时,那些迭代伊始密度就较小的单元,整个迭代过程单元密度始终呈减小趋势,将在最终采用的结构中删除.这些单元的密度由于没有小到计算机视为0的程度,因此每一步迭代计算都会消耗大量的计算资源.而那些迭代伊始密度就较大的单元,整个迭代过程单元密度亦始终保持较大或不断增大趋势,将在最终采用的结构中保留.
假设一个较小的密度阈值,若优化产生小于这一阈值的密度单元时,即将这些单元密度以极小值ε替代,视其为空洞,这样就可以提高迭代计算的收敛速度.实际上,这些单元并不是空洞单元,是有一定密度的,若将其人为设定为空洞单元,则材料质量约束计算时这部分质量将不存在,这将使得替代后的总质量大大小于替代前的总质量.虽然从约束上讲,这是可以接受的,但与实际情况不符,且计算时极有可能出现“早熟”等畸形收敛,计算结果将难以接受.因此,再给出一个较大的密度阈值,将小于这一阈值的单元密度以这一阈值替代.这种替代有2个优点:一是解决了删除较小密度单元带来的替代后总质量过小的问题;二是替代后单元密度值更为集中,剩余单元间密度差异减小,避免了收敛速度过快造成的畸形收敛,这就可在加速迭代的基础上最大程度地保证结构拓扑优化迭代计算的稳定性.为了区别2个密度阈值,本文将较小的密度阈值称为MFS,较大的密度阈值称为MFL.
以图1说明改进迭代算法的原理.图1(a)显示了微结构单元的密度曲线L,横坐标n为微结构单元数量,纵坐标 ηi为第i个微结构单元密度,单元密度在0~1之间.图1(b)显示了替代前微结构单元的密度曲线L,阴影部分显示的面积为总的单元质量.图1(c)显示了用MFS和MFL2个密度阈值进行替代的微结构单元的密度曲线L,阴影部分显示的面积仍为总的单元质量,但此总的单元质量要小于或等于图1(b)所示的总的单元质量.

图1 改进迭代算法的原理Fig.1 Principles of modified iterative method
2 改进迭代算法的流程和算式
改进迭代算法的流程如图2所示.图中:Ws0为初始做结构材料质量;Wsl为使用密度阈值替代后微结构材料质量.
对式(2)进行修正,得到改进迭代算法的算式,即


图2 改进迭代算法的流程Fig.2 Flow chart of modified iterative method
3 算例及分析
3.1 算例1
图3(a)所示为2m×2m的矩形平面结构,材料弹性模量为20GPa,左侧边界固定,右侧下部作用一铅直向下的集中荷载P=1kN.图3(b)所示为有限元网格,结构共划分为40×40个矩形单元.
删除率选择为80%,极小值ε取0.001.首先采用结构拓扑优化均匀化方法的一般迭代算法进行计算,计算结果如图4所示,保留的微结构单元密度为0.1~1;然后采用改进迭代算法进行计算,计算时 MFS取0.1,MFL取0.4,计算结果如图5所示.

图3 算例1Fig.3 Plan and meshes of Example 1

图4 算例1一般迭代算法的计算结果Fig.4 Results of Example1 of general iterative method

图5 算例1改进迭代算法的计算结果Fig.5 Results of Example 1 of modified iterativemethod
采用一般迭代算法,共需迭代48步.为了能够清楚地看出计算过程,图中显示了密度大于0.1的单元.而实际上,在一般迭代算法的计算中,除了密度小于极小值的单元外,其余所有单元都是参与计算的.对于密度为0.1~1的微结构单元,随着迭代的不断进行,其有限单元的数量会不断减少,达到优化目标时迭代结束.
采用改进迭代算法,共需迭代19步.由于MFS取为0.1,因此选择显示的单元密度为0.1~1.
比较图4(a)和图5(a)可知,当S=6步时,改进迭代算法的结果比一般迭代算法的结果外形更为光滑.图5(b)显示,当S=11步时,改进迭代算法的结果已非常接近于最终优化结果.而对于一般迭代算法来说,迭代30步的结果也与最终的优化结果有较大差异.图4(c)与图5(c)相比,外形上两者结果基本一致,仅结构个别部位有微小差异.随着结构复杂性和荷载的增加以及MFS和MFL取值的不同,这些微小差异会有所增大.由于采用了不同的算法,这些微小差异是不可避免的,因此,当出现这些微小差异时,可认为优化计算结果一致.
从本例来看,改进迭代算法和一般迭代算法的优化计算结果一致,而其迭代步数仅为一般迭代算法的40%左右,计算时间较一般迭代算法减少50%以上,且计算时占用的计算资源大大减少,这使得复杂的大型结构在拓扑优化计算时可以采用更细小的网格.
3.2 算例2
采用不同的MFS和MFL进行计算,并根据计算结果给出MFS和MFL的取值范围,以避免因密度阈值的不确定而过多地耗费时间.
图6所示为1.6m×1m的矩形平面结构,材料弹性模量为20GPa,3个集中荷载(P1=P2=P3=1kN)作用于结构的下边界.结构共划分为64×40个矩形板单元,下方左右两端受固定约束.删除率取为80%,极小值ε取为0.001.图7给出了一般迭代算法的计算结果.不同MFS和M FL取值改进迭代算法的计算结果如图8所示.
从图8(a)~(d)可知,在 MFL相同的情况下,随着 MFS的增大,迭代步明显减少,且当MFS和MFL取值都较大时,迭代收敛情况明显优于MFS和MFL取值较小时的收敛情况.
从图8(b)~(e)可知,在 MFS相同的情况下,随着 MFL的增大,迭代步也相应减少,减少的幅度较M FL相同而M FS增大情况下的幅度小很多.图8(b)与(c)显示的结果可认为是一致的.图8(d)与(e)的 MFS和MFL取值均比图8(b)和(c)大,但从优化结果来看,并非仅有微小差别,由于算例结构和荷载的简单性,这里不能再认为两者的优化结果一致.图8(e)的结果从单元数量来说,明显比图8(d)的要少.这一差别主要体现在结构中部受荷载区域.该区域内的V形结构较为单薄,这一结果是不可用的.由于其脆弱部分很少,可以人为地进行弥补.
图8(f)给出了一个MFS和MFL都较大的极端情况,在此情况下,拓扑优化计算迭代仅需9步,但结果却很不理想.其主要问题是优化得到的结构V形区域部分十分脆弱,有较多单元都是通过角连接的,不能为设计人员所接受.

图6 算例2平面结构Fig.6 Plan of Example2

图7 算例2一般迭代算法的计算结果Fig.7 Results of Example 2 of general iterative Method

图8 算例2改进迭代算法的计算结果Fig.8 Results of Example 2 of modified iterativemethod
4 结 论
a.当M FS和M FL取值合理时,拓扑优化均匀化方法的改进迭代算法所需要的迭代步数远小于一般迭代算法,收敛速度也大为提高.
b.从理论上讲,一般迭代算法的计算过程是没有人为干预的,所得优化结果应该是最合理的;而改进迭代算法的计算过程受到人为的干预,干预程度与MFS和MFL的取值大小有关,这种干预势必会影响优化结果的合理性.但是从算例的计算结果来看,当MFS取0.1,MFL取0.3时,改进迭代算法得到的优化结果与一般迭代算法得到的优化结果相似程度最高.因此,当M FS和M FL取值合理时,改进迭代算法计算过程干预对优化结果的影响可以忽略.
c.当 MFS和 MFL取值合理时,增大 MFS和 MFL均会提高收敛速度,而增大 MFS对提高收敛速度的作用要比增大MFL对提高收敛速度的作用大.当MFL相同时,MFS的微小变化也会对迭代步数产生较大影响;而当M FS相同时,增大M FL尽管也可以加速收敛,但是对迭代步数不会产生决定性影响.
d.M FS取值范围定为0.1~0.2,M FL的取值范围定为0.3~0.45比较合理.对于大型计算来说,迭代过程中MFS和MFL的取值可以根据计算实际情况在一定范围内进行调整,这可以加速收敛.
e.本文对拓扑优化均匀化方法的一般迭代算法进行了改进,为了加强对迭代过程的控制,引入了2个密度阈值,并给出了密度阈值的建议取值范围.算例表明,这一改进迭代算法可行,当采用合理的密度阈值时,拓扑优化计算收敛速度会明显提高.
[1]TALICHI C,PAULINO G H,LE CH.Honeycomb wachspress finite elements for structural topology optimization[J].Structural and Multidisciplinary Optimization,2009,37(6):569-583.
[2]GUO X,YAMAZAKIK,CHENGG.A new approach for the solution of singular optimain truss topology optimizationwith stress and local buckling constraints[J].Structural and Multidisciplinary Optimization,2001,22(5):364-373.
[3]MAIERG,BUACA C,PATTAVANA A.Topology-information periodic updates in multi-domain ASON networks with topology aggregation[J].Fiber and Integrated Optics,2008,27(4):265-277.
[4]FITZWATERL,KHALIL R,HUNTER E,et al.Topology optimization risk reduction[C]//Annual Forum Proceedings-AHSInternational,AHS International 64th Annual Forum.Montreal,Canada:American Helicopter Society,2008:543-556.
[5]张忠中,苏超.结构拓扑优化方法在拱式渡槽拱轴线设计中的应用[J].河海大学学报:自然科学版,2007,35(4):444-447.(ZHANGZhong-zhong,SUChao.Continuum topology optimizationmethod for arch axisdesign of arciform aqueducts[J].Journal of Hohai University:Natural Sciences,2007,35(4):444-447.(in Chinese)).
[6]BENDEOEM P,KIKUCHI N.Generatingoptimal topologies in structural design usinga homogenization method[J].Computer Methods in Applied Mechanics and Engineering,1988,71(2):197-224.
[7]BENDSOE M P,MOTA S.Topology design of structures[M].NATO ASI:Kluwer Academic Publishers,1993.
[8]HASSANI B,HINTON E.A review of homogenization and topology optimization I:homogenization theory for media with periodic[J].Computers&Structures,1998,69:707-717.
[9]BENDSOEM P,SIGMUNDO.Material interpolations in topology optimization[J].Archiveof Applied Mechanics,1999,69:635-654.
[10]YOUN SK,PARK S H.A study on the shape extraction process in the structural topology optimization using homogenized material[J].Computers&Structures,1997,62(3):527-538.
[11]BREMICKERM,KIKUCHI N,CHIREHDAST M,et al.Integrated topology and shape optimization in structural design[J].Journal of Structural Mechanics,1991,19(4):551-587.

