莱布尼兹型级数的推广

张洪光

（赤峰学院 数学系，内蒙古 赤峰 024000）

莱布尼兹型级数的推广

张洪光

（赤峰学院 数学系，内蒙古 赤峰 024000）

定义了k项交错级数和广义莱布尼兹型级数，推广了莱布尼兹定理，证明了级数的收敛性，给出了一类特定形式的一般项级数收敛性的判定定理.

k项交错级数；莱布尼兹型级数；收敛

1 引言

级数理论是数学分析的主要内容之一，数项级数敛散性的判别是最基本的教学内容，莱布尼兹给出了交错级数敛性的判别方法，但对于任意项级数的判别无能为力.本文推广了莱布尼兹定理，得到了特定形式的一般项级数收敛性的判定定理.

（1）{un}单调减少，即un+1≤un(n=1,2,3,…)

则称该级数为莱布尼兹型级数.

2 主要结果

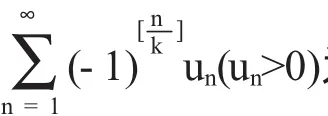
（1）∃N，∀n＞N，un+1≤un

则该级数收敛.

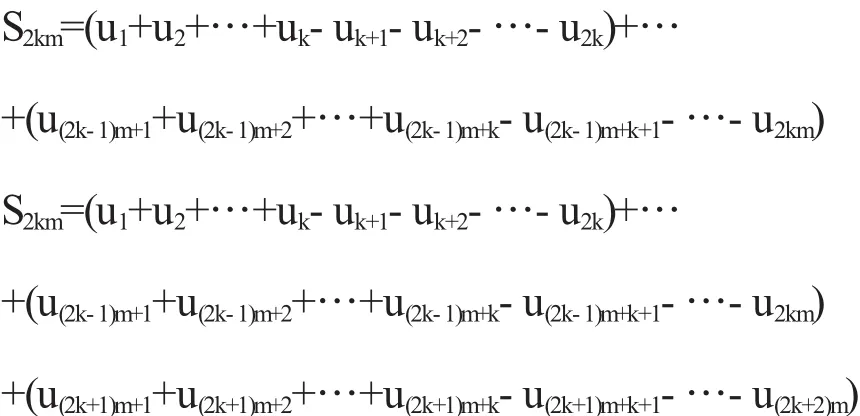
由条件（1）知{S2km}单调增加，另一方面{S2km}有界.由单调有界数列必有极限定理知数列{S2km}极限存在

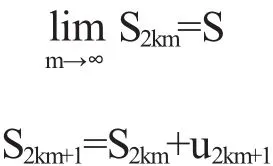
再由定理的条件（2），得到

同理

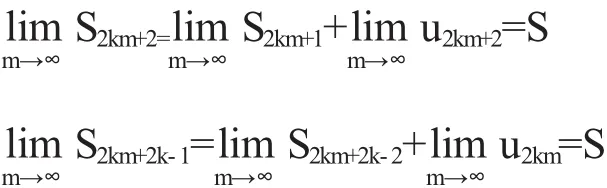
由此知{Sn}收敛.

定义4若任意项级数

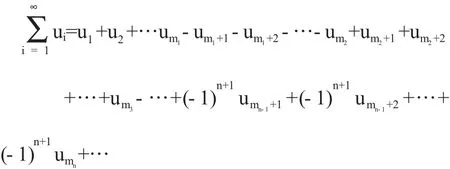
满足以下两个条件：

（1）∃N，∀n＞N，An+1≤An(n=1,2,3,…)，

则称该级数为广义莱布尼兹型级数.其中

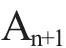
对∀ε＞0，∃N，∀n＞N，∀p∈N有

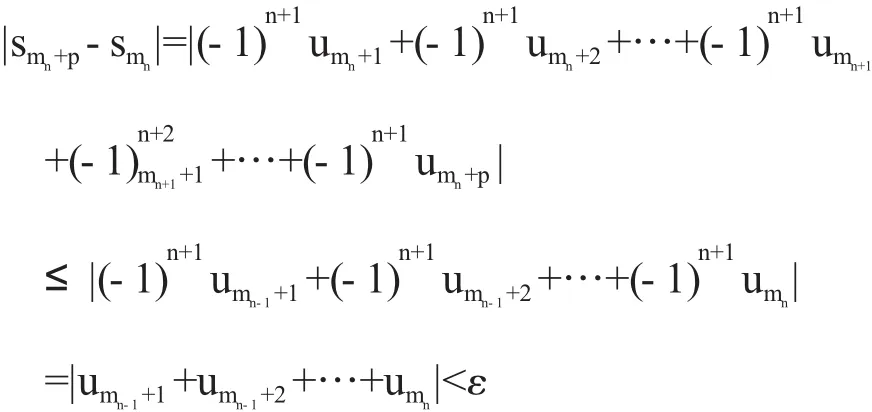
〔1〕刘玉涟，傅沛仁.数学分析讲义（下）[M].北京：高等教育出版社,1981.

〔2〕毛纲源.高等数学解题方法技巧归纳(下册)[M].武汉：华中科技大学出版社.

〔3〕华东师大数学系.数学分析[M].高等教育出版社.

O173.1

A

1673-260X（2010）02-0009-02