成品油二次配送优化研究*

苏 娟，王 岳，许 坤

成品油二次配送优化研究*

苏 娟1，王 岳1，许 坤2

（1.辽宁石油化工大学石油天然气工程学院，辽宁抚顺113001；2.辽河油田茨榆坨工程技术处作业一公司，辽宁盘锦124010）

我国关于成品油物流、配送领域的优化还处于起步阶段，配送方案还存在很多问题，为了降低二次配送过程中油品的损耗，节省二次配送费用，合理的安排车型和路线具有实际意义。以分仓式大容量罐车分点装卸为例，建立合理安排车型和最短路线（TSP问题）两阶段数学模型，并采用lingo软件和遗传算法进行求解，得出合理的车型和路线安排。

成品油；二次配送；优化

我国的成品油物流费用与国外相比一直居高不下，在成品油配送和运输路径优化方面存在巨大潜力[1]。成品油配送方式主要有铁路、管道、公路、水路4种。由于成品油运输的高危险性对其运输工具提出了非常严格的技术要求，需要专门的管道、油轮、铁路或公路罐车进行输送，成品油具有流动性和易挥发的特点，非常适用于管道运输。但是由于我国管道业起步较晚，尤其是成品油管网覆盖率较低，为了降低二次配送过程中油品的损耗，分仓式大容量罐车在成品油二次配送中逐渐被接纳。目前配送公司存在车辆结构差，运力不足，重复、低效、空驶率等问题，使运输无法实现优化。为了提高车辆运输效率，依据加油站一定周期需求规律，利用运载量大的车辆在往返线路上为加油站提供相同或不同的油品，既可以降低油品的损耗，又可以节省配送费用。

目前，在配送优化模型方面，主要有TSP问题和路由问题两种较为成熟[2]。关于旅行推销员问题（TSP）的扩展MTSP更适合配送优化问题，但只限于同种车型的配送问题[3]，为解决不同车型配送问题，本文提出不同车型的TSP问题，建立优化模型并求解，使其更能满足实际要求。

1 数学模型

1.1 合理安排车型，最小费用流模型

配送中心合理的安排车型为周围加油站送油，能够节约资源。以总的配送费用最小为目标，满足加油站需求的前提下，合理选择车型。

目标函数及约束条件如下：

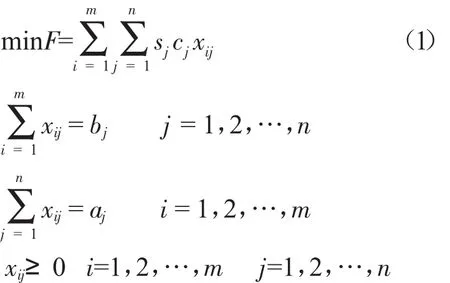
式中：F—配送费用，元；

ai—i车型的最大载重量，t；

m—车型的种类；

n—加油站的个数；

sj—配送中心到加油站j的距离，km；

cj—配送中心到加油站j的单位运价，元/（t·km）；

xij—第i型车到第j个加油站的配送量，t；

bj—加油站的需求量，t。

1.2 最短路（TSP）问题模型

配送线路的合理组织是配送的一个重要环节，有益于物流运动的合理化，有益于指导资源的合理配置，并能直接降低物流的成本[4]。最短路问题即第一阶段选定车型后，每种车型为固定的多个加油站送油，车辆如何行驶，才能使总的距离最短。

目标函数和约束条件如下：

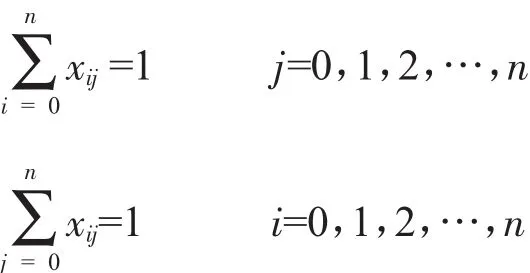
式中：L—车辆行驶总的距离，km；

n—加油站的个数；

dij—配送中心到加油站及加油站之间的距离，km。

2 实例分析

某配送中心，周围8个加油站，Z1Z2Z3Z4Z5Z6Z7Z8，配送中心有3种车型y1y2y3，最大载运量分别为：40，45，36 t。配送中心到加油站的单位运价（t·km）为0.3元，配送中心到加油站及加油站之间的距离见表1。0代表配送中心。选择适合的车型为加油站送货，并确定每种车型的最佳行驶路线。

表1 配送中心到加油站及各加油站之间的距离表Table 1 Table of distances between service stations km

由最小费用流模型，利用lingo软件进行求解得到的最小费用为：832.95元，得到的调运方案如表2。

由第一阶段优化结果，得到车型y1，y2负责配送的加油站之间及加油站与配送中心之间的距离如下：见表 3，表 4。

表2 运量分配平衡表Table 2 The balance sheet on carryings t

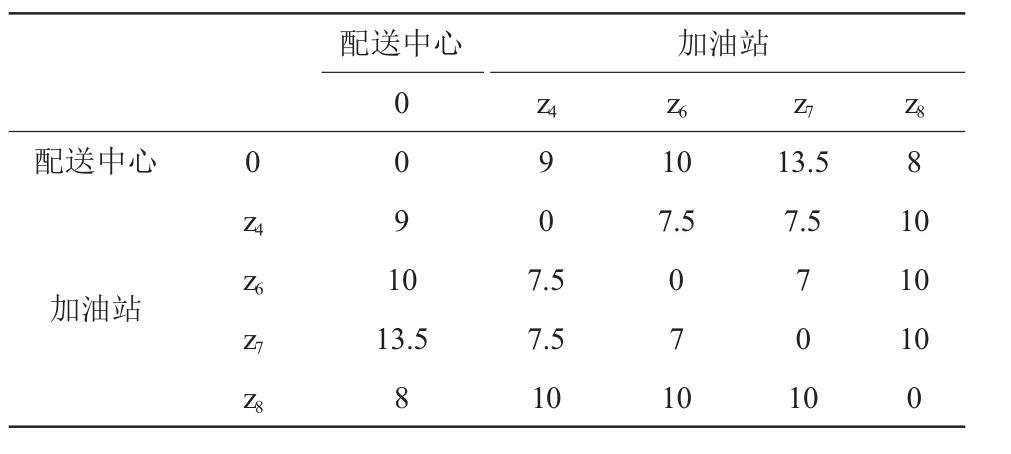
表3 y1负责配送的加油站、配送中心之间距离Table 3 Table of distances between service stations from y1 km

由TSP问题优化模型，利用遗传算法求解，取种群规模n=10；叠代次数c=50；淘汰指数m=2；alpha=0.8。最后得到车辆最佳的路线安排：

优化的结果：

y2车型行驶的路线0—4—6—7—8—0，最短距离为41.5 km；

y3车型行驶的路线0—2—5—3—1—0，最短距离为29 km。

表4 y2负责配送的加油站、配送中心之间距离Table 4 Table of distances between service stations from y2 km

3 结论

本文以降低配送过程中油品损耗和最小化配送费用为基础，对配送过程中车型的选择和路线的安排进行了研究，建立合理安排车型和最短路线（TSP问题）两阶段数学模型，并采用lingo软件和遗传算法进行求解，得到了能够降低成品油配送费用的有效方案。该优化模型为企业进行成品油二次配送提供了理论依据。

[1]王 华.成品油物流优化DPO模型的应用研究[J].当代石油石化，2004，12（12）：24-27.

[2]胡运权，郭耀煌.运筹学教程[M].北京：清华大学出版社，2000.

[3]宋杰鲲，张在旭，张宇.成品油配送路线优化问题[M].油气储运，2008，27（11）：28-30.

[4]庄大海，梁 威，安 娜.优化成品油配送体系[J].中国石油企业，2005（7）：60-61.

[5]蔡光跃，董恩清.遗传算法和蚁群算法在求解TSP问题上的对比分析[J].计算机工程与应用，2007，43（10）：96-98.

Study on Optimization of Refined Oil Second Distribution

SU Juan1，WANG Yue1，XV Kun2
（1．LiaoNing ShiHua University，Liaoning Fushun 113001，China；2.LiaoHe Oil Field，Liaoning Panjin 124010，China）

China in the field of optimizing refined oil logistics and distribution is still at the initial stage，distribution plan still exists many problems.To reduce the loss of oil and save distribution costs，reasonable arrangements about routes and models during the second distribution process are very necessary.In this paper，taking sub-bunker large-capacity tanker as an example，two stages of the mathematical model for reasonable choices of vehicle types and the shortest route （tsp problem）was established，then this problem was solved by lingo software and genetic algorithm，and reasonable vehicle type and the shortest route were obtained.

Refined oil；The second distribution；Optimization

TE 834

A

1671-0460（2010）05-0538-03

2010-05-12

苏 娟（1982-），女，辽宁凌海人，现辽宁石油化工大学石油天然气工程学院硕士在读，研究方向为成品油物流优化。E-mail：aiaisxk_008@163.com。