海杂波背景下基于混沌理论的目标检测

韩长喜，李宗武，武 楠，徐艳国

(南京电子技术研究所，江苏 南京 210013)

海面目标检测技术在军用和民用中均占有重要的地位，提供准确的目标判决是对海雷达工作的重要任务之一。雷达自动检测系统依据判决准则在给定的检测阈值下做出判决，而强海杂波往往成为微弱目标信号的主要干扰。如何处理海杂波将直接影响到雷达在海洋环境下的检测能力。

海杂波是指雷达照射下海面的后向散射回波，雷达检测海杂波背景下目标的常用方法是将海杂波模拟成具有某种概率分布的随机过程(如Rayleigh分布、Log-normal分布、Weibull分布、K分布等)，而判决通常采用贝叶斯(Bayes)假设检验。传统的检测技术由于统计决策理论中检测概率和虚警概率之间固有的矛盾，因而在强海杂波和低虚警概率条件下发现弱小目标(如小船、小冰块)的能力有限。因此，如果能够在一定程度上抑制海杂波的干扰，将有可能在很大程度上改善雷达的目标检测性能。

在海杂波背景下雷达目标检测领域的最新研究中，研究人员得出海杂波不完全是一种随机的信号，而是具有混沌的许多典型特征[1-5]。其中以HAYKIN S领导的研究小组为代表，他们利用大量的海上实测数据研究了海杂波的混沌特性，并利用混沌技术对传统的雷达信号处理进行了新的探索，积累了许多富有积极意义的研究成果，为海杂波背景下的目标检测提供了一种新的研究途径[1，6-8]。本文以混沌理论为基础，以神经网络为工具，从相空间重构理论出发，利用RBF神经网络来重构海杂波的内在动力学，引入基于预测误差的检测方法对正弦信号进行检测分析。这种新的检测技术具有优于传统检测技术的应用潜力，因为它充分利用了海杂波具有混沌行为这一先验信息，而混沌系统是一种确定性系统，是可预测的，至少在短时间内具有可预测性。

1 海杂波的混沌建模

通常采集到的海杂波信号是一个时间间隔为Δt的序列c(n)(n=1，…，N)，该时间序列是产生海杂波的多变量非线性混沌系统的观测量。Takens从理论上证明了用混沌系统的一个观测量可以重构出原动力系统模型，而且重构出的模型与用来重构的信号成分无关[2]。

根据Takens嵌入定理，存在1个非线性映射φ，使式(1)成立：

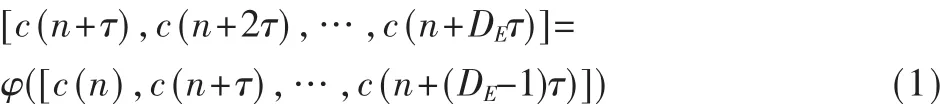
式(1)表明，等号左边的各个分量由等号右边的分量共同决定，并且只有 c(n+DEτ)是新的信息，因此存在非线性函数，满足式(2)：

式(2)中，F(·)为产生海杂波的混沌系统，DE为嵌入维数，τ为延迟时间。嵌入维数和延迟时间是重构混沌动力系统的两个重要参数，本文采用伪最近邻(GFNN)方法计算嵌入维数[11]，交互信息法(MI)计算延迟时间。

由式(2)可以看出，利用观测时间序列重建混沌动力系统的问题转化为一步预测问题，式(2)就是海杂波预测模型。

由此可见，用原系统的观测量来重构相空间，主要在于函数F的建模。神经网络具有很好的学习和逼近非线性函数的能力，由于c(n+DEτ)与等式右边的所有分量都存在一定的关系，所以用它们作为模式对训练神经网络，凭借神经网络的强大学习能力，可以得到非线性映射F赞：RDEτ→R1，使F赞逼近 F。

神经网络有2种工作模式：训练模式和工作模式。将海杂波的一段用作训练数据，使神经网络收敛，即网络中线性部分和非线性部分的诸权值均收敛到稳定值，这是神经网络的训练模式。工作模式，即用作预测器时，神经网络的权值保持不变，观测数据依序输入到神经网络中，网络的输出就是混沌序列的预测值。

神经网络的基本类型有前馈型、自组织型和随机网络等。而常用的前馈型网络有径向基(RBF)神经网络和多层感知器(MLP)，BP网络是典型的多层感知器，与BP网络相比，要实现同一个功能，RBF神经网络的神经元个数可能要比BP网络的神经元个数多。但是，RBF神经网络所需要的训练时间却比前向BP网络少，加之RBF神经网络具有最佳逼近性能，不存在局部极小点等优点[12]。本文的实验中采用RBF神经网络对海杂波进行训练和预测。

RBF神经网络是由输入层、隐含层和输出层构成的3层前向网络，如图1所示。输入层由信号源结点组成；第2层为隐含层，隐单元数由所描述的问题的需要而定，隐含层采用径向基函数作为传递函数；第3层为输出层，它对输入模式的作用产生响应。从输入层空间到隐含层空间的变换是非线性的，而从隐含层空间到输出层空间的变换是线性的。

图1 RBF神经网络结构

RBF神经网络的传递函数radbas是以输入向量和权值向量之间的距离‖dist‖作为自变量的，其原型函数为：

随着权值向量和输入向量之间距离的减少，输出是递增的，当输入自变量为0时，函数取得最大值为1。

为了使RBF神经网络的训练样本能够提供更多的信息，本文确定输入层神经元数为DEτ，隐含层神经元数由训练误差和训练样本数共同决定，输出层只有1个神经元。

RBF神经网络的训练过程分为2步：第1步为无教师式学习，用来确定输入层与隐含层间权值w1；第2步为有教师学习，用来确定隐含层与输出层间权值w2。在训练以前，需要提供输入矢量X、对应的目标矢量T以及径向基函数的扩展常数C。训练的目的是求取两层的最终权值 w1、w2和阈值 b1、b2。

2 混沌海杂波背景下的目标检测

在海杂波具有混沌特性的理论基础上，通过重构海杂波的相空间，并利用神经网络的学习和预测能力来预测下一个时刻的回波信号，将预测到的信号与实际接收到的雷达回波信号相比较，根据预测误差检测目标信号。这样就把从强海杂波中检测微弱目标信号的问题转化为从预测误差中检测目标信号的问题。检测的步骤如下[6-10]：

(1)用RBF神经网络对杂噪比高的海杂波数据建模，将神经网络作为一个预测器，即用混沌背景产生模式对输入矢量X、对应的目标矢量T训练RBF神经网络，通过调节扩展系数C和训练误差，使其预测误差最小，此时的神经网络就称为训练好的神经网络。

(2)利用训练好的神经网络预测一个无目标回波数据 x0(n)(n=1，…，M)，得到预测值x赞0(n)(n=1，…，M)，计算预测误差：ε0(n)=|x赞0(n)-x0(n)|(n=1，…，M)，根据 ε0(n)的直方图计算出海杂波混沌预测误差的概率密度函数pc(x)，然后在给定的虚警概率Pfa下，由式(4)可以得出阈值η。

(3)对于某一接收信号 x(n)(n=1，…，M)，利用训练好的神经网络预测下一个回波数据x赞(n)(n=1，…，M)，并与实际接收到的回波数据作比较，计算预测误差：ε(n)=|x(n)-x赞(n)|。

(4)将 ε(n)与 η 比较，若 ε(n)>η，则认为有目标，否则无目标。

检测框图如图2所示。

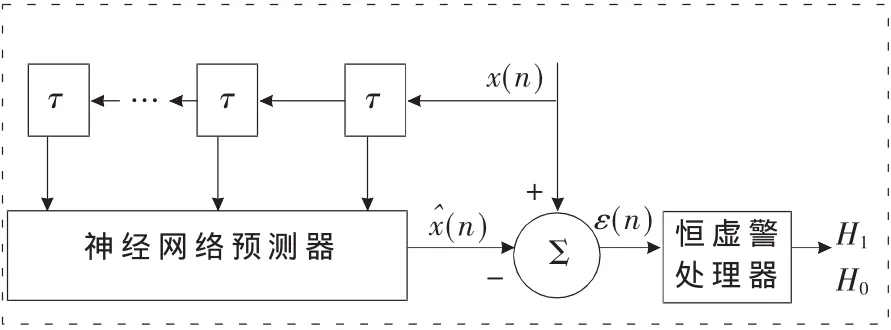
图2 基于神经网络的检测方法

3 仿真实验结果与讨论

本实验所采用的数据是由雷达采集的实测海杂波数据，雷达为X波段的宽带相参雷达，工作在低仰角凝视状态。选择距离门280、长度为1 536点的数据，记为c(n)(n=1，…，1 536)作为实验数据，经幅度和相位校正后，如图3所示。用其前 1 024点记为c1(n)(n=1，…，1 024)作为训练样本，后 512点记为 c2(n)(n=1，…，512)作为测试样本。

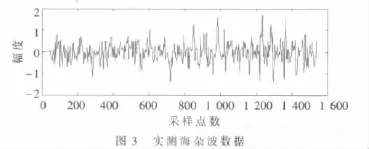
用交互信息法和伪最近邻法分别计算该数据的时间延迟 τ和嵌入维 DE，得 τ=5，DE=9，因此输入层神经元数为45，输出层神经元数为1。

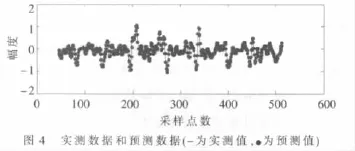
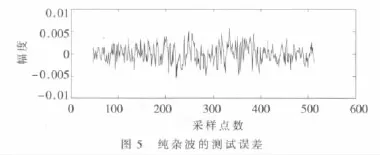
将训练样本送入RBF神经网络对网络进行训练，通过调节训练误差和扩展系数，使测试误差(单步预测误差)最小，图4为实测数据和预测数据的对比，图5为训练好的网络的测试误差。从图5可以发现，测试误差大部分在 5×10-3之内，均方差 MSE=3.597 8×10-6，这说明该网络已经获得了海杂波的内在动力特性，且具有很好的泛化能力，此时的网络就称为训练好的神经网络。则可以根据给定的虚警概率Pfa计算门限η。

在测试样本 c2(n)(n=1，…，512)的第 100点加入 1个幅度为 4.559 8×10-3的脉冲，计算得到此时的信杂比为-40 dB。经神经网络处理后，得到预测误差如图6所示，在第102点有1个尖峰，此处的信杂比为3.389 8 dB(用该点)，即经神经网络处理后，信杂比改善了43.3898dB。

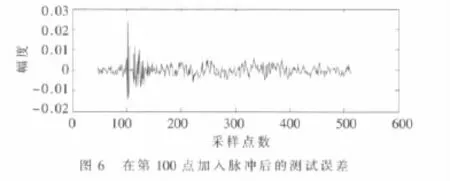
图7为测试误差经单元平均横虚警处理的结果，由图可见，在第102点检测到目标。

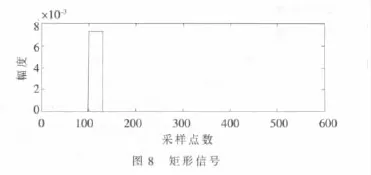
在测试样本 c2(n)(n=1，…，512)的第 100点到第129点加入1个幅度为7.226 8×10-3的矩形信号，矩形信号如图 8所示，矩形信号加 c2(n)(n=1，…，512)，如图 9所示。计算得到此时的信杂比为-36 dB。

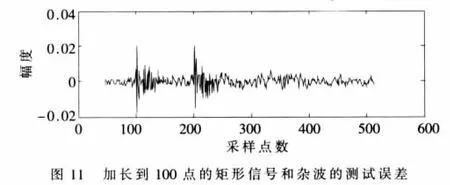
经RBF神经网络处理后得到测试误差如图10所示，在矩形信号的起点和终点附近(即第102点和131点)测试误差较大，在其他点测试误差相对较小。随着矩形信号长度的增加，这种现象表现得越明显，图11为其他条件不变时，矩形信号加长到100点时的测试误差。从第140到第195点的测试误差几乎与没有信号加入时相同。

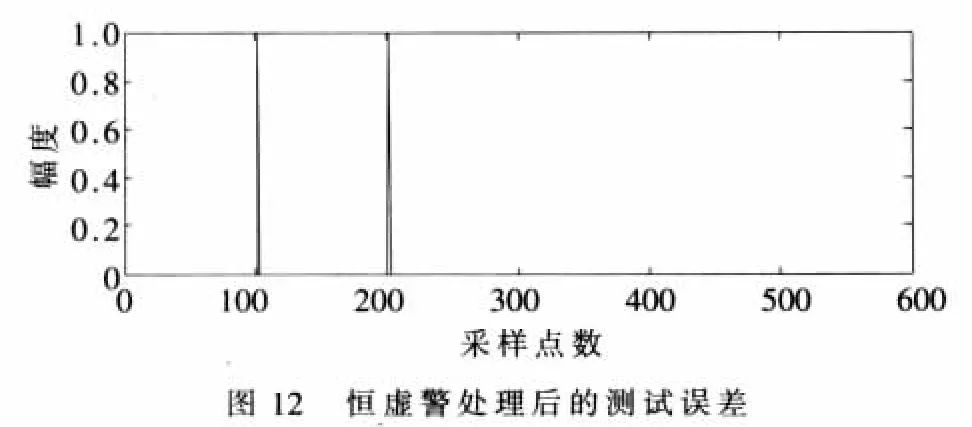
将杂波加长度为100的矩形信号的测试误差进行恒虚警处理，结果如图12所示，可以发现，只能在矩形信号的起点和终点附近的第102点和202点检测到目标。

本文是建立在海杂波具有混沌特征的理论基础上，通过相空间重构技术，利用RBF神经网络预测器的学习和对非线性函数的逼近能力，获取海杂波的内在动力学。根据确定性混沌系统的短期可预测特点获得单步预测误差，通过对脉冲信号和不同长度的矩形信号的处理分析，得到基于混沌的处理方法对微弱脉冲信号的信杂比改善可达43.389 8 dB，能够检测到微弱脉冲信号。而矩形信号只在信号的起点和终点附近得到类似的信杂比改善和检测能力，其中的各点信杂比改善较小，在这些点检测不到目标，且随着矩形信号长度的增加，这种现象越明显。由此可以得出，基于混沌的检测方法对脉冲信号比对矩形信号的检测能力强。

[1]HAYKIN S，XIAO B L.Detection of signals in chaos[J].Proceeding of the IEEE， 1995，83(1)：95-122.

[2]HAYKIN S，PUTHUSSERYPADY S.Chaotic dynamics of sea clutter：an experimental study[J].Radar 97， 1997， 14-16：75-79.

[3]HAYKIN S， BAKKER R， CURRIE B W.Uncovering nonlinear dynamics-the case study of sea clutter[J].Porceeding of the IEEE， 2002， 90(5)：860-881.

[4]赫金.海杂波的混沌特性分析[M].祝明波，译.北京：国防工业出版社，2007.

[5]林三虎，朱红，赵亦工.海杂波的混沌特性分析[J].系统工程与电子技术，2004，26(2)：178-180.

[6]LEUNG L T.Chaotic radar signal processing over the sea[J].IEEE Journal of Oceanic Engineer， 1993，18(3)：287-295.

[7]XIAO B L，HAYKIN S.Chaotic detection of small target in sea clutter[M].IEEE， 1993：I-237-I240.

[8]BHATTACHARYA T K，HAYKIN S.Neural network-based radar detection for an ocean environment[J].IEEE Transaction on Aerospace and Electronic System.1997，33(2)：408-420.

[9]陈瑛，罗鹏飞.海杂波背景下基于RBF神经网络的目标检 测[J].雷 达 科 学 与 技 术 ， 2005，3(5)：271-275.

[10]张亚飞，朱敏慧.基于混沌理论和形态学变换的海面分布目标检测[J].数据采集与处理，2008，23(2)：123-128.

[11]MATTHEW B K， REFFIE B， HENRY D I.Determining embedding dimension for phase-space reconstruction using a geometrical construction[J].Physical review A.1992，6(45)：3403-3411.

[12]张德丰.MATLAB神经网络应用设计[M].北京：机械工业出版社，2009.