基于边集数组的最小独立闭合环搜索算法实现

叶 宝,陈 义

(1.同济大学土木工程学院,上海 200092;2.苏州工业园区测绘有限责任公司,江苏苏州 215021)

基于边集数组的最小独立闭合环搜索算法实现

叶 宝1,2,陈 义1

(1.同济大学土木工程学院,上海 200092;2.苏州工业园区测绘有限责任公司,江苏苏州 215021)

控制网的闭合差检验是平差计算前的一个重要步骤,目的是发现原始观测数据中的粗差并予以剔除,并评估外业观测的质量。根据测量控制网的数据结构特点,提出基于边集数组存储结构的控制网最小独立闭合环搜索算法的实现原理及具体过程。最后通过不同算例对算法的正确性进行验证。

数据结构;边集数组;最小独立闭合环;算法

一、引 言

在测量平差计算前,为保证平差结果的正确性,防止观测值可能含有粗差及系统误差影响平差结果,无论是传统的测量控制网,如导线网、水准网,还是 GPS控制网,都需对控制网中的各种多边形闭合差进行检核,以探测、剔除粗差,并评定观测值的质量。因此,如何自动搜索出控制网的最小独立闭合环成为一个核心问题。最小独立闭合环搜索算法目前主要有三种：基于邻接矩阵变换算法、基于生成树和余树变换算法、基于深度优先搜索算法[1]。一般都要用到数据结构知识,采用邻接矩阵或邻接表等存储结构来实现。本文根据控制网的特点,采用了更为直观的边集数组的存储结构,对生成树和余树变换算法进行了编程实现,并通过不同的例子,验证了算法的正确性。

二、控制网的数据结构

1.数据结构的概念

数据结构是相互之间存在一种或多种特定关系的数据元素的集合。数据结构包含数据和数据关系两方面的基本特征。

如图 1所示,根据数据元素之间关系的不同特性,通常有四类基本数据结构：集合结构、线性结构、树形结构、网状结构。数据结构包括数据的逻辑结构 (logic structure)和物理结构 (physical structure)。其中数据的物理结构包括数据元素的表示和存储以及数据元素之间关系的表示和存储。通常数据结构采用数组法、邻接表法、十字链表、邻接多重表等基本的存储结构表示。

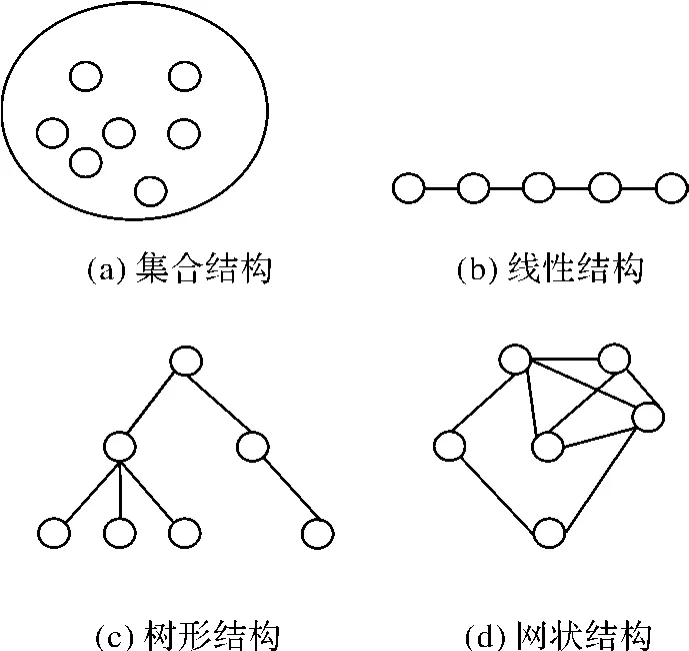
图1 基本类型的数据结构

2.控制网的数据结构分析

根据图 1和对测量控制网的特点分析,显然控制点之间是任意的、多对多的复杂关系。因此控制网与数据结构中的网状结构的概念一致。通过比较,可以建立控制网和图之间如表 1所示的概念映射关系。

表 1 测量控制网与图的概念间的映射关系

对于测量控制网而言,可以采用图的邻接矩阵等存储结构表示。考虑到测量控制网的特点,总是由一系列控制点和边组成的网状结构,因此可以从图的定义出发,采用点集数组和边集数组的存储结构(包括数据元素和数据元素关系的存储)。二者均采用结构体数组,点集数组存储控制点的所有信息,边集数组存储边的所有信息,则所有控制点间的观测值和相关关系都通过边集数组来反映,如表 2所示。

表 2 测量控制网结构体数组存储结构

三、算法原理分析

1.最小独立闭合环搜索的概念

最小独立闭合环是指控制网中含有观测边数最少且相互独立的多边形闭合环。是对控制网进行各种闭合差检验、定位粗差的基础几何模型。如前所述,测量控制网可映射为图 (网)的数据结构。则问题的核心即归结为对网的结构进行的最小独立闭合环的分析确定。其内涵有二：①所搜索确定的闭合环最小,也即环的边数最小,与网的“最短路径”的概念一致;②各闭合环相互独立,亦即每一个环中都至少有一条不属于其他环的边[2]。需要指出的是,对于一个网而言,其最小独立闭合环的组合、构成情况并不唯一,只要找出其中的一组即可满足定位粗差及评定观测值质量的需要。

2.生成树、余树变换算法的原理

网的最小独立闭合环搜索算法中以生成树、余树变换算法最为基础,且搜索结果稳定[3]。该算法采用逆向思维,其原理是：首先对控制网进行简化处理,将其“修剪”为一个称为生成树的树形结构。所谓生成树就是一个连通图的最小连通子图,其特点是含有图中的全部 n个顶点,但只有足以构成一棵树的 n-1条边,如果在生成树上添加一条边,则必定构成一个环,因其使得它所依附的两个顶点之间有了第二条路径。因为测量控制网中不存在孤立的控制点,各点之间总是通过一定的观测量、观测边发生着联系,因此,对控制网而言,其总是一个连通网,对应的总是可以化简为一棵生成树。如图2所示。

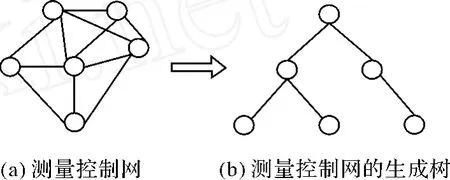
图2 控制网数据结构转化示意图

因此,对于一个网,总可以通过一定的算法,将其分割为两个部分,一是生成树;二是生成树的补集,称为余树,其中的每一条边称为余枝。将每一条余枝回代添加到生成树上时,即构成一组闭合环,取其中路径最短者为该余枝对应的闭合环,则全部余枝分别回代即构成一组独立闭合环,因为根据“独立”的定义,每个余枝对应的闭合环均至少有一条边(余枝本身)不属于其他环。为保证各闭合环是最小环,需要定义余枝添加到生成树上的次序规则。

1)尝试将全部余枝添加到生成树上,取其中闭合环路径长度最短者,优先添加到生成树上,作为当前最小闭合环;

2)在生成树的添加余枝后的当前子图上,尝试将其余的余枝添加到当前子图上,取其中闭合环路径长度最短者,优先添加到生成树上,作为当前最小闭合环;

3)重复以上过程,直到所有 r个余枝均添加到生成树上,即得到一组 r个最小独立闭合环。

四、算法实现过程

基于生成树和余树变换算法的实现过程,控制网采用点集数组 P[n]和边集数组 L[m]的结构存储(均为结构体数组)。

1)采用BFS(宽度优先遍历)算法,得到控制网的一棵宽度生成树,生成树也采用点集数组、边集数组存放,则生成树的点集与控制网的点集相同,边集为控制网边集的子集,将控制网的边集设为全集,则生成树边集的补集即为生成树的余树的边集数组。编程中只要将 BFS遍历经过的边的 V isited值标定为 true,即表示生成树,否则为 false表示余树,此即实现了对控制网边集数组的分割处理。

2)将余树中的余枝 (边集数组 L[m]中 V isited值为 false的边)逐一回代、添加到生成树上(边集数组L[m]中 V isited值为 true的边),每添加一个余枝,得到一组闭合环,通过网的最短路径算法求得该余枝两端点间的最短路径,比较所有余枝的最短路径,选择最短路径最小的余枝,优先添加到生成树上 (将其边的Visited值标定为 true)。

3)重复2),直至所有的余枝都添加到生成树上为止(边集数组L[m]中所有边的Visited值均为 true)。

由上述过程可见,关键是基于边集数组的最短路径算法的实现。本文采用经典的 Dijkstra算法,其实现过程是：定义两个一维工作数组,一个是最短路径长度数组 PathLength[n],此数组与点集数组P[n]相互对应,用以存放起始点 (余枝的一个端点)到生成树中各顶点的路径长度;另一个是最短路径点名数组 PathName[n],用以存放起始点到其余各顶点的最短路径的点序列。

1)初始化 PathLength[n]和 PathName[n]数组：起始点 S到其自身的边长为 0,与其不相邻接的点的边长置为∞,与其相邻接的点,通过一个成员函数 GetEdge(string PointA,string PointB),求出起始点到该点的边的长度,并在点集数组 P[n]中将起始点 S的 Visited值标定为 true,表示起始点即默认为已知的最短路径终点。

2)扫描 PathLength[n]数组：查找该数组中当前的最小值,凡是在点集数组 P[n]中 V isited值为true的点,其对应的在 PathLength[n]数组中的值均不予考虑,而在剩余的数组元素中查找最小值,并将其对应的在点集数组 P[n]中的点的 Visited值标定为 true,表示该点为自起始点出发的、当前最短路径的终点,在 PathName[n]数组中记录下该点 T,并记录当前最短路径值MinPath。

3)更新 PathLength[n]和 PathName[n]数组：以 2)中得到的当前最短路径终点 T作为新的参考点,循环遍历点集数组 P[n],查找计算 T点到达其他Visited值为 false的点的边长 (P[n]中 Visited值为 true的点可视为已知最短路径终点点集,不予考虑),如果遍历的点与 T点相邻接,并且MinPath与该点到 T点的边长之和小于其在 PathLength[n]中的该点到起始点 S的路径长度,则用MinPath与该点到 T点的边长之和更新 PathLength[n]中该点到起始点 S的当前最短路径长度值。

4)重复步骤 2)～步骤 3),直至点集数组P[n]中点的 V isited值全部为 true,即起始点到所有顶点的最短路径均已查找得到,全部顶点均加入到已知最短路径终点点集中为止。

最后需要说明的是关于成员函数 GetEdge (string Poin tA,string PointB),该成员函数的作用是分析网中各顶点是否相邻及邻接的边长值,用以代替邻接矩阵。用此函数省却了复杂的构造邻接矩阵的过程,并且避免了当网的顶点较多时,随着邻接矩阵的快速膨胀,需要大量占用内存空间的问题。其实现过程为,通过遍历边集数组L[m],分析确定出各顶点相邻与否及邻接的边长值。对于无向图,只要边的起点和终点之间有一向相通即可视为相邻,对有向图,需要起点和终点之间双向连通,才可视为相邻。

五、应用及验证

本文应用上述原理,采用 C#语言进行了编程实现。并采用几个算例对算法的正确性进行验证。

图3为某市三等水准网,对该水准网进行闭合环搜索计算,共计算得到水准闭合环 23个,与原水准网中闭合环的实际情况完全一致;统计计算出的闭合环长度、闭合差均与水准网实际情况全部完全一致。采用其他几个算例,同样取得了准确的搜索计算结果。

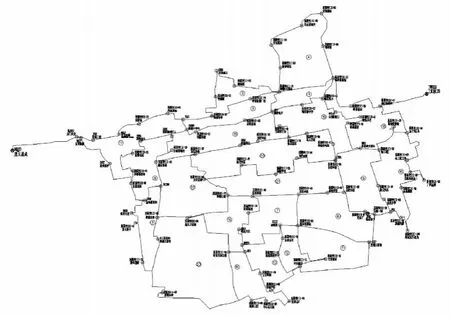
图3 算例

六、结束语

本文根据测量控制网的特点,采用点集数组和边集数组的存储结构,实现了对网的最小独立闭合环的自动搜索。避免了使用大矩阵,占用大量存储空间的问题产生,并且使得数据的存储结构更直观、易于理解,便于数据的输入存储管理。可应用于实际生产及软件设计中。

[1] 赵一晗,伍吉仓.控制网闭合环搜索算法的探讨[J].铁道勘察,2006,32(3)：12-14.

[2] 王金岭,李陆勋.控制网最小闭合环信息自动生成算法[J].测绘通报,1995(1)：11-15.

[3] 邹进贵,冯晨.控制网最小独立闭合环搜索算法研究[J].地理空间信息,2008,6(6)：97-99.

[4] 冯琰,张正禄.最小独立闭合环与附合导线的自动生成算法 [J].武汉测绘科技大学学报,1998,23(3)：255-259.

[5] 武汉测绘科技大学.测量平差基础[M].3版.北京：测绘出版社,1996.

[6] WATSON K,NAGEL C,等.C#入门经典[M].3版.北京：清华大学出版社,2007.

[7] 严蔚敏.吴伟民,等.数据结构[M].C语言版.北京：清华大学出版社,2007.

Algorithm of Searching forM in imum Independent Closed-loop Based on Array of Edge Set

YE Bao,CHEN Yi

0494-0911(2010)12-0037-03

P207

B

2009-12-10

叶 宝(1977—),男,宁夏盐池人,硕士生,研究方向为大地测量及测量数据处理。