精度可控的CRT工业机器人几何建模

李 吉 平， 朱 华 伟， 杜 江

( 1.大连工业大学 信息科学与工程学院， 辽宁 大连 116034;2.大连工业大学 机械工程与自动化学院， 辽宁 大连 116034 )

0 引 言

天津中环三津公司的CRT自动线共包含10台工业机器人，分别负责对CRT生产过程中不同工艺过程的处理。该生产线需要完成10多种不同规格CRT产品的生产。以图形方式，在计算机上进行CRT工业机器人控制代码的正确性检验，对提高生产效率、保证生产质量具有重要意义。CRT工业机器人的几何建模是控制代码图形验证的技术基础之一，是本文的研究内容。

机器人虚拟模型的建立是机器人遥操作[1]、离线编程[2]和运动仿真[3-4]的基础，针对上述应用的机器人几何建模已取得了许多研究成果[1-4]。但这些方法的共同问题是：无法控制模型的表达精度。就CRT自动线而言，当验证自动线各设备的协同效果时，参与仿真的设备较多，为提高验证效率，不需要精确地几何描述；当验证个别工艺过程时，需要根据验证目的，确定相应的模型表达精度，以获得精度和效率的平衡。因此，模型精度的按需控制是本文方法的特点所在。

为便于精度控制，在分析CRT工业机器人组成结构[5-6]的基础上，提出了基于离散表达[7]的CRT工业机器人几何建模方法。

1 几何分解

CRT工业机器人是由相互独立的不同部件组成的装配体，包括运动部件和静止部件。不同部件都具有明确的物理意义。为方便实现CRT工业机器人的几何建模，需要将CRT工业机器人逐级分解为若干容易造型的基本体。具体分解准则包括：

(1)设备分解准则。CRT工业机器人的各运动部件在物理上存在依存关系，但相互间的空间位置可能发生变化，是不同的对象。该准则将CRT工业机器人分解为不同运动部件，体现了相应的运动装配关系。

(2)部件分解准则。由“(1)”得到的运动部件通常是由多种机械零件通过某种方式(如：螺钉)固联在一起。各零件虽然在物理上相互固联，仍需在建模时当作不同对象来处理，以体现固定的装配关系。

(3)复杂零件分解准则。由“(2)”得到的零件有时仍比较复杂，利用CAD进行造型时会消耗大量时间，需将其进一步分割为简单的基本体。基本体组成零件的关系也可视为固定的装配关系，只是各基本体不具有真正的物理意义。

按照上述准则，可以将CRT工业机器人最终分解成若干基本体，如：长方体、圆柱体、圆锥体和球体等，然后再用CAD软件对这些基本体进行造型，这种方法不但快捷，还有利于后续的离散处理工作。

2 离散处理

基本体的离散处理是实现CRT工业机器人几何精度可控的关键。曲线、曲面的离散会产生离散误差，而离散误差的大小是衡量离散结果是否合适的标准。

2.1 完整曲面片的离散

用离散点间的线性插补来近似表达曲面是离散误差εs产生的原因，可通过控制离散点的采样密度将εs调整到误差允许的范围内。

完整的曲面片在参数空间是规则的四边形，但参数空间的矩形映射到笛卡儿空间后，通常会发生形状改变。为方便离散点的位置计算和误差控制，根据文献[7]论述，采用二叉子分割法，将参数空间的子分割与笛卡儿空间的误差控制相结合，实现完整曲面片的离散化处理。完整曲面片首先在参数空间经二叉树方法划分为若干矩形区域，然后通过检查矩形区域在笛卡儿空间的边长和对角线与曲面间的误差εs是否在允许误差内，来控制参数空间的子分割是否需要继续：εs在误差范围内，停止分割；否则，继续。

2.2 剪切曲面片的边界处理

对剪切曲面而言，在完成“2.1”所述离散处理后，还需要对剪切边界曲线作进一步处理。完整曲面经子分割形成的参数矩形按与边界曲线的关系被标志为不同的状态：

(1)IN: 参数矩形在剪切边界曲线内；

(2)OUT: 参数矩形在剪切边界曲线外；

(3)ON: 参数矩形与剪切边界曲线相交。

对标志为ON的参数矩形，求其与边界曲线的交点，并线形连接，属于曲面的部分标志为IN，否则标志为OUT。

剪切曲面是通过将所有标志为OUT的部分删除后得到的。

2.3 离散点集的三角形化

经“2.1”和“2.2”可得到任意曲面片的离散点集。为方便数据的可视化，还需要对离散点集进行三角形化处理。

对参数矩形，可通过其最短对角线将其划分为2个三角形。但是，如果参数矩形的边界有悬挂点(悬挂点由二叉子分割形成，如图1中的黑色圆点所示)，需要在参数矩形的中心加入1个新的离散点(图1中的黑色方点)，然后将该中心点和参数矩形的4个顶点以及所有悬挂点线形连接。

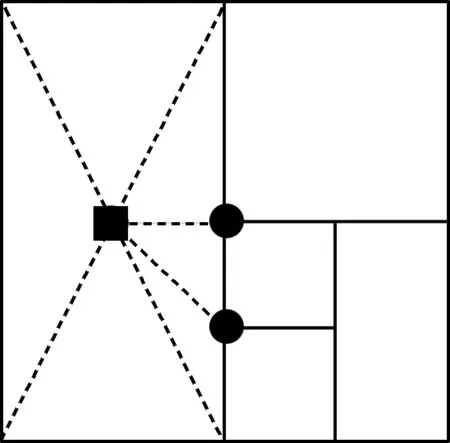
图1 悬挂点的处理Fig.1 Dealing with the dangling nodes

2.4 离散数据的组织

在三角形化过程中，将离散点有机地组织在1个数据结构中，有利于后续工作对离散信息的查询和利用。比如：对CRT工业机器人发生碰撞的区域用指定颜色实时显示，就需要对相应的离散点和三角面片进行可视化处理，效果会比文献[5]中的单纯文本信息提示更直观。

离散数据存储用数据结构由若干离散点的队列组成。这些点列只存储与某离散点相关的其他离散点的信息，并按逆时针方向排列，如图2所示。图2(a)为经三角形化后的某曲面模型，图2(b)为相应离散点的组织结构。该结构包含了三角形网格的所有必要信息，可以方便地找到与某给定点、边或三角形相邻的所有其他点、边或三角形。

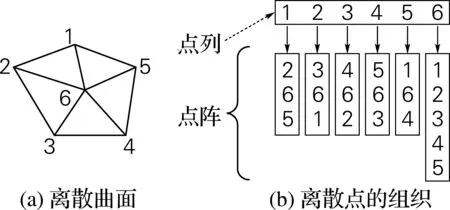
图2 离散数据的组织Fig.2 Organization of discrete data

3 原型软件系统开发与测试

根据上述方法，利用DirectX图形库和C++编程语言实现了CRT工业机器人几何建模的原型软件系统。

图3为CRT工业机器人吸盘部件在不同离散误差条件控制下的三角化结果。从图3可见，离散误差对离散点个数的影响很大，会直接影响到模型的表达精度和图形验证的运行速度。

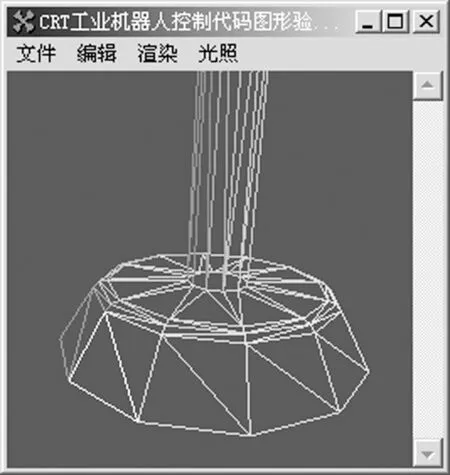
(a) εs=0.5 mm

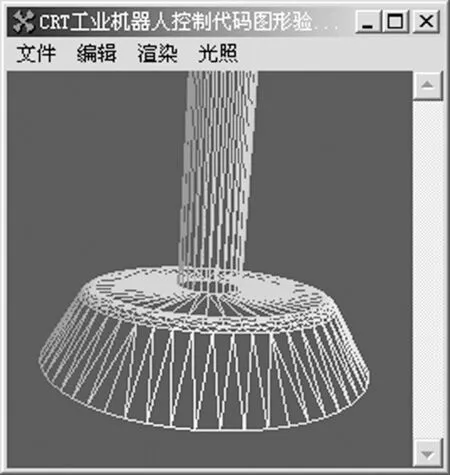
(b) εs=0.1 mm图3 离散举例Fig.3 Discretization example

将离散后的基本体按几何分解过程作反向操作，即可得到图4所示的CRT工业机器人几何模型。

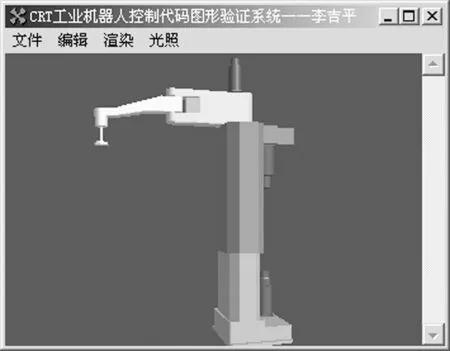
图4 CRT工业机器人几何模型Fig.4 Geometric model of CRT industrial robot

4 结 论

本文研究了CRT工业机器人的几何建模问题，提出了CRT工业机器人的三级分解准则，并重点论述了模型的离散处理方法，其中涉及完整曲面片的离散、剪切曲面的边界处理、离散点集的三角形化和离散数据存储的数据结构等内容。作为CRT工业机器人运动控制图形仿真软件的基础，该方法便于工程技术人员灵活控制机器人的几何表达精度，满足了CRT生产中不同工艺过程对仿真精度和效率的不同要求。

基于本文方法的原型软件系统，已用于天津中环三津公司CRT工业机器人控制系统的开发过程中[6]，对缩短开发周期，减少开发过程对实际生产的影响起到了至关重要的作用。

[1] 倪涛,赵丁选,倪水,等. 基于虚拟现实的遥操作工程机器人图形仿真[J]. 农业机械学报, 2005, 36(5):80-82.

[2] 汤新华,DREWS P. 机器人三维可视化离线编程和仿真系统[J]. 焊接学报, 2005, 26(2):64-68.

[3] 马志强,陈一民,汪地. 面向对象的机器人仿真与监控系统[J]. 计算机工程与设计, 2005, 26(1):75-78.

[4] LAUE T, SPIESS K, ROFER T. SimRobot-A general physical robot simulator and its application in RoboCup[J]. Lecture Notes in Computer Science, 2006, 4020:173-183.

[5] 李吉平,耿梦,施殿波,等. CRT工业机器人控制代码的碰撞检测[J]. 大连工业大学学报, 2009, 28(1):69-72.

(LI Ji-ping, GENG Meng, SHI Dian-bo, et al. Collision detection of control code for CRT industrial robot[J]. Journal of Dalian Polytechnic University, 2009, 28(1):69-72.)

[6] 李吉平,施殿波,耿梦,等. CRT工业机器人控制系统的开发[J]. 大连工业大学学报, 2008, 27(4):336-340.

(LI Ji-ping, SHI Dian-bo, GENG Meng, et al. The development of CRT industrial robot’s control system[J]. Journal of Dalian Polytechnic University, 2008, 27(4):336-340.)

[7] 李吉平,刘华明,任秉银. 基于曲面离散技术的加工精度检验方法的研究现状[J]. 机械研究与应用, 2000, 13(2):7-9.