一种自动拟合变差函数的改进遗传算法

刘小军，汪 欣，焦丽莉

(1.嘉兴学院 数学与信息工程学院，浙江 嘉兴 314001；2.黄山学院 现代教育技术中心，安徽 黄山 245041)

作为地质统计学所特有的基本工具，变差函数的计算和拟合是储层随机模拟中的一个必须有且重要的步骤，但是一直没有很好的解决方法。通常人们采用人工拟合方法，但这种方法不仅效率较低而且缺乏统一客观的标准。王仁铎等提出用加权回归多项式方法来拟合变差函数球状理论模型的参数，把变差函数的自动拟合问题向前推进了一步，但是没有解决参数的正负号问题；矫希国等提出用线性规划法拟合变差函数球状理论模型的参数，由线性方程组非负解的理论解决模型参数的正负号问题，但该方法对各实验变差函数值等同对待，没有强调前面的几个数据点，给拟合结果带来较大的误差；冯国庆等把遗传算法应用到实验变差函数的拟合中，但该算法一方面对各实验变差函数值等同对待，另一方面采用二进制编码方式，降低了拟合的精度；李少华等提出对线性规划法做进一步改进，用滞后距的倒数作为线性规划法中的权系数，再用单纯形法来进行求解，这样做避免了对各实验变差函数值等同对待和理论模型参数的正负号等问题，但用单纯形法求解常常需要引入人工变量，增加了计算工作量和自动拟合的复杂度[1]。基于这种情况，通过研究尝试用改进的遗传算法来自动拟合变差函数，此方法不仅以滞后距倒数为权系数的线性规划法建立目标函数，还对各求解步骤进行改进，取得了较好的效果。

1 变差函数

变差函数[2-3]是对空间变化的属性参数随距离变化率的一种度量，反映了空间变异程度随距离变化的特征。它有多个理论模型，常用的理论模型有：球形模型(Spherical)、指数模型(Exponential)、高斯模型(Gaussian)等，其中球形模型(Spherical)的一般形式为：

式中，C0为块常数，C(0)=C0+C为基台值，C称为拱高，a为变程。本算法实现的变差函数的自动拟合就是在选择了变差函数理论模型的基础上，根据已有的实验变差函数值拟合出所选模型中这些参数(C0，C0，a)的值。

2 遗传算法

2.1 基本的遗传算法

遗传算法[4](简称为GA)是模拟生物在自然界的遗传和进化过程而形成的一种算法。它采用简单的编码技术来表示各种复杂的参数，并通过对一组编码进行简单的遗传操作和优胜劣汰的自然选择来指导搜索方向。主要由以下几部分组成：

1)编码，在遗传算法中把一个问题的可行解，即从其解空间转换到遗传算法所能处理的搜索空间的转换方法就称为编码。

2)选择算子，用来从种群中选择亲代个体的选择概率，以便产生新的子代个体。

3)交叉算子，交叉是核心的遗传操作，也是产生新个体的主要方法。它是通过两个父代染色体交换某些基因来完成的，一般取0.4～0.99。

4)变异算子，是指将个体染色体编码串中的某些基因座上的基因值，用该基因座其他等位基因来替换，从而形成一个新个体的概率，一般取0.0001～0.1。

2.2 改进的遗传算法

2.2.1 目标函数构建

文献[1]通过以滞后距的倒数作为权系数的线性规划法来建立目标函数，在降低计算复杂度的同时又强调了前面的几个数据点。但在实际应用中，滞后距的值往往较大，用其倒数作为权系数会降低甚至忽略当前数据点的作用，文献[1]中虽提到用一个常量来放大权系数，但在拟合时仍需手工设置，为了提高拟合的自动化在此对取值用如下式子来计算：

m=max(hi)×10

(2)

则结合文献[1]中的结果，本算法构建的目标函数如下：

约束条件为：0≤C0≤M，0≤C≤N，0≤a≤T。

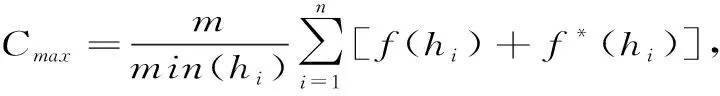
2.2.2 编码方法

运用遗传算法的关键在于如何选择合适的编码方式来表示问题的解。本算法采用浮点数编码，即对决策变量的真实值进行编码，与传统的二进制编码方法相比，此方法更适合于表示范围较大、精度要求较高的遗传算法中，提高了拟合的精度和效率。

2.2.3 选择算子

进行选择操作是为了避免基因缺失，本算法中按适应度大小，通过将本代最优个体替换本代最差个体的方式保留本代最优个体直接进入下一代，而在下一代中继续参与交叉和变异操作，其余个体按轮盘赌进行随机选择。这样既使用了最优保存策略保护了最优个体，但又避免了某个局部最优个体不易被淘汰掉反而快速扩散对全局搜索能力的影响，保证了算法的收敛性。

2.2.4 交叉算子

算术交叉的操作对象一般为由浮点数编码所表示的个体，所以本算法采用算术交叉策略，实现简单又提高了效率。

2.2.5 变异算子

图1 实验变差函数值

变异能改善遗传算法的局部搜索性能，变异率设置不当，有可能破坏优良个体或使算法最终收敛到局部最优。本文算法对自适应变异率进行改进，通过某种条件判断种群的状态，不同的状态采用不同的变异率，避免了变异概率选取的盲目性[4]。具体变异公式如下：

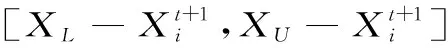
3 实例计算

在此以文献[5]中的数据和模型为例，并与其结果进行对比，具体数据如图1所示：

首先，确定决策变量和约束条件。此实例中决策变量为球形模型中的三个参数：C0，C和a，为了方便对比，取与文献[5]相同的区间，即：C0∈ [0, 5]，C∈ [0, 10]，a∈ [0, 10000]。

第二步，确定权系数及建立目标函数。根据式(2)、(3)计算有：m= 80000,Cmax= 24908，且在满足上一步骤得到的约束条件下，可得如下目标函数：

f(x)=24908-80x4-53.34x5-40x6-32x7-26.67x8-22.86x9-20x10-17.78x11

-16x12-15.54x13-13.33x14-12.31x15-11.43x16-11.43x16-10.67x17-10x18

第三步，确定算法运行参数。本算法中需要的算法运行参数有群体大小M、交叉概率Pc、变异概率Pm以及终止代数T。在此使用默认参数值，依次为60,60, 0.8和 0.005。

对上述问题用本文算法进行求解，可得球状理论模型(图2(a))如下：

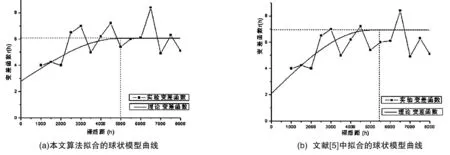
图2 球形模型拟合曲线对比

图3为本文算法四次执行本实例计算过程中，遗传代数和适应度值之间的关系：

图3 球形模型计算过程

4 结论

利用改进遗传算法进行变差函数的自动拟合，不仅与实际地质情况相结合，在充分重视变差函数前面几个点的同时又没有降低或忽略剩余点；而且针对实际问题用浮点数编码等策略对传统遗传算法进行改进，通过与文献[5]中的结果比较，说明本算法在很大程序上提高了拟合效率和收敛的速度，取到了较好的效果。

[参考文献]

[1] 李少华,张昌民,马玉震.线性规划法自动拟合变差函数的改进[J].江汉石油学院学报,2001，23(z1):36-37.

[2] 王家华,高海余,周叶.克里金地质绘图技术—计算机的模型和算法[M].北京:石油工业出版社，1999.

[3] 曾闽山.基于微机的储层地质三维可视化建模软件设计和实现技术[D].北京:中国矿业大学研究生学位论文,2007.

[4] 郑生荣,赖家美,刘国亮,等.一种改进的实数编码混合遗传算法[J].计算机应用,2006,26(8):1959-1962.

[5] 冯国庆,周涌沂,李允,等.利用遗传算法拟合实验变差函数[J].西南石油学院学报,2005,27(2):23-25.