介质陶瓷谐振器的参数测量

曹良足 郭童军

（景德镇陶瓷学院机电学院，江西景德镇333403）

介质陶瓷谐振器的参数测量

曹良足 郭童军

（景德镇陶瓷学院机电学院，江西景德镇333403）

介绍一种测量TEM型介质陶瓷谐振器的频率和Q值的方法。在谐振器的开路端加载高Q值的电容，分别与网络分析仪的输入端和输出端进行弱耦合，用标量网络分析仪测出其传输曲线，从传输曲线上直接读出回路谐振频率和有载Q值。从理论上分析了测量值与理论值的差距，得到了谐振器的频率和无载值的计算公式。用介电常数为74的BaO-TiO2-Sm2O3微波介质材料制作了介质陶瓷谐振器，将测量数据与反射法进行比较，结果表明该方法测量精度较高。

介质陶瓷谐振器，谐振频率，无载Q值

1 引言

介质同轴谐振器（简称TEM型谐振器）是由低损耗、高介电常数的微波介质陶瓷制成的，因而具有较高的Q值和较小的体积，广泛用于微波滤波器、双工器和振荡器[1]。准确测量谐振器的参数，如谐振频率和Q值，对谐振器的生产和应用大有帮助。国内外关于TEM型谐振器参数测量的文献报道较少，反射法是测量谐振频率和无载Q值的最常见的方法之一[2]，借助Smith Chart(史密斯圆图)确定临界耦合点（即谐振点），但是需要使用矢量网络分析仪。Raymond S.kwork等[3]介绍了一种用标量网络分析仪测量谐振器无载Q值的方法，但需要求出变换函数（mappingfunction），该函数的求解相当繁琐。作者曾采用串联谐振法测量TEM谐振器的参数[4]，该方法简便易行，但谐振频率的测量值与实际值相差一个常数，适用于谐振器的分选。本文采用一种新的测量方法：在谐振器的开路端加载电容分别与网络分析仪的输入和输出端进行弱耦合，并测量其传输曲线，从传输曲线上读出回路的谐振频率和有载Q值，然后经过计算得到谐振器的频率和无载Q值。

2 测量原理

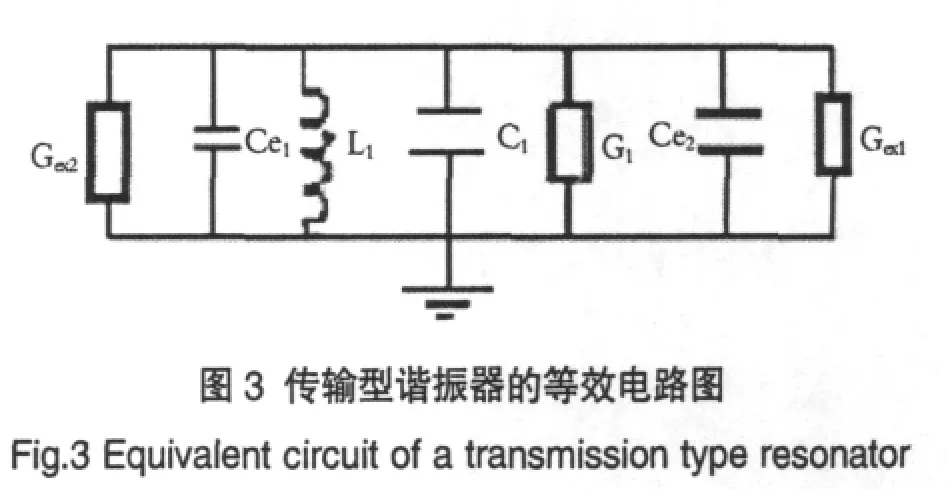
1/4波长介质同轴谐振器等效为并联LC谐振回路[5]，按图1所示线路进行测量。

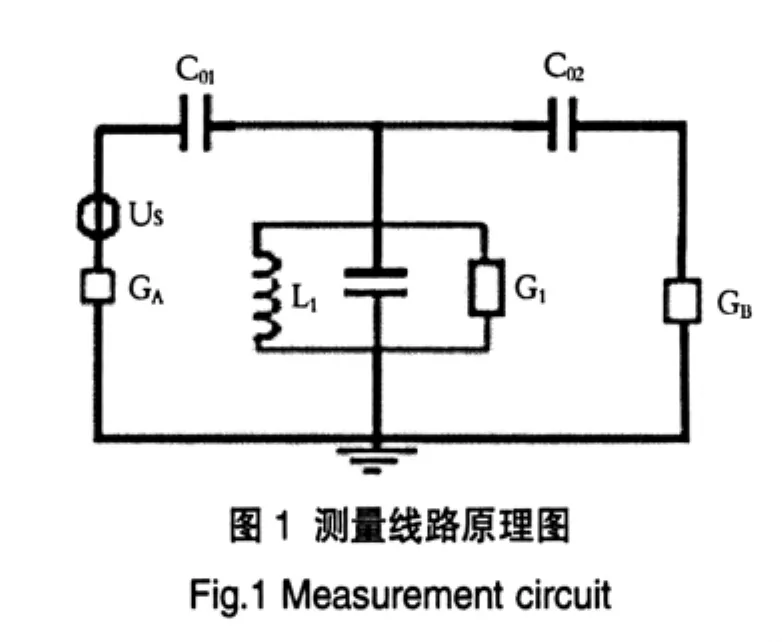
图1中C01和C02为输入输出耦合电容,GA和GB分别为信号源和负载的导纳，一般为0.02S，Us为信号源。由C1、L1和G1构成的并联回路就是谐振器的等效电路。另外图中的耦合电容为高Q值，所以假设它们为理想电容器。

现将图1进行导纳变换[6]，得到图2。

图2中J01和J02为导纳倒置变换器，Ce1和Ce2分别为导纳变换所产生的补偿电容，Ce1和Ce2由下列公式求得[7]：

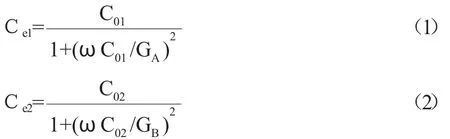
将上述电路的谐振回路进一步化简得到传输型谐振器的等效电路图[7]，如图3所示。

图3中Gex1和Gex2分别为输入和输出导纳通过导纳变换后的导纳。Gex1和Gex2分别由下式求出：

上述式中β1和β2分别为输入耦合系数和输出耦合系数。

对图3，输入导纳由下式求出：

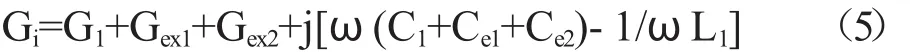
当谐振器发生谐振时，Gi等于实数，便得到谐振频率：

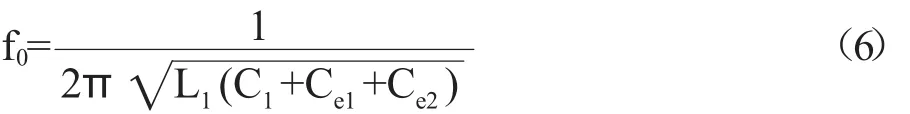
传输型谐振器的QL值由（3）、（4）、（5）和（6）式求出：

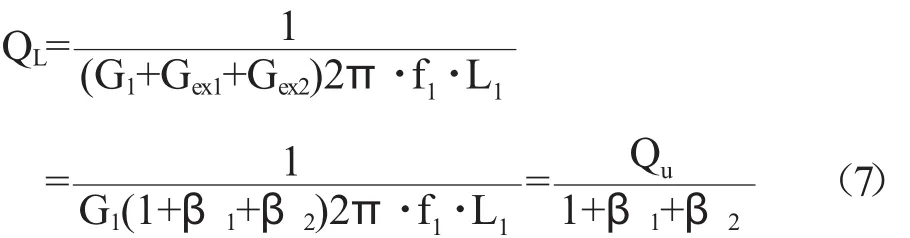
（7）式中Qu为谐振器的无载Q值，QL的大小可以从图4所示传输曲线上读出：要想求Qu的值，必须知道β1和β2的值，β1和β2也与传输曲线上的插入损耗IL有关，它们的关系式如下[7]：

当β1=β2时，将（9）式代入（7）式得到Qu的表达式：

当Ce1和Ce2很小时，并假设Ce1=Ce2＝Ce，将（1）、（2）和（6）式用幂级数展开[8]，并忽略高次项得：

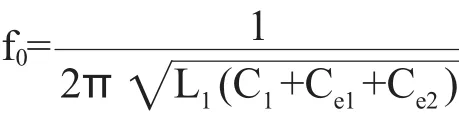
当C01很小，（11）式的第三项可以忽略不计，则(11)式可简化为

3 试验过程及结果讨论

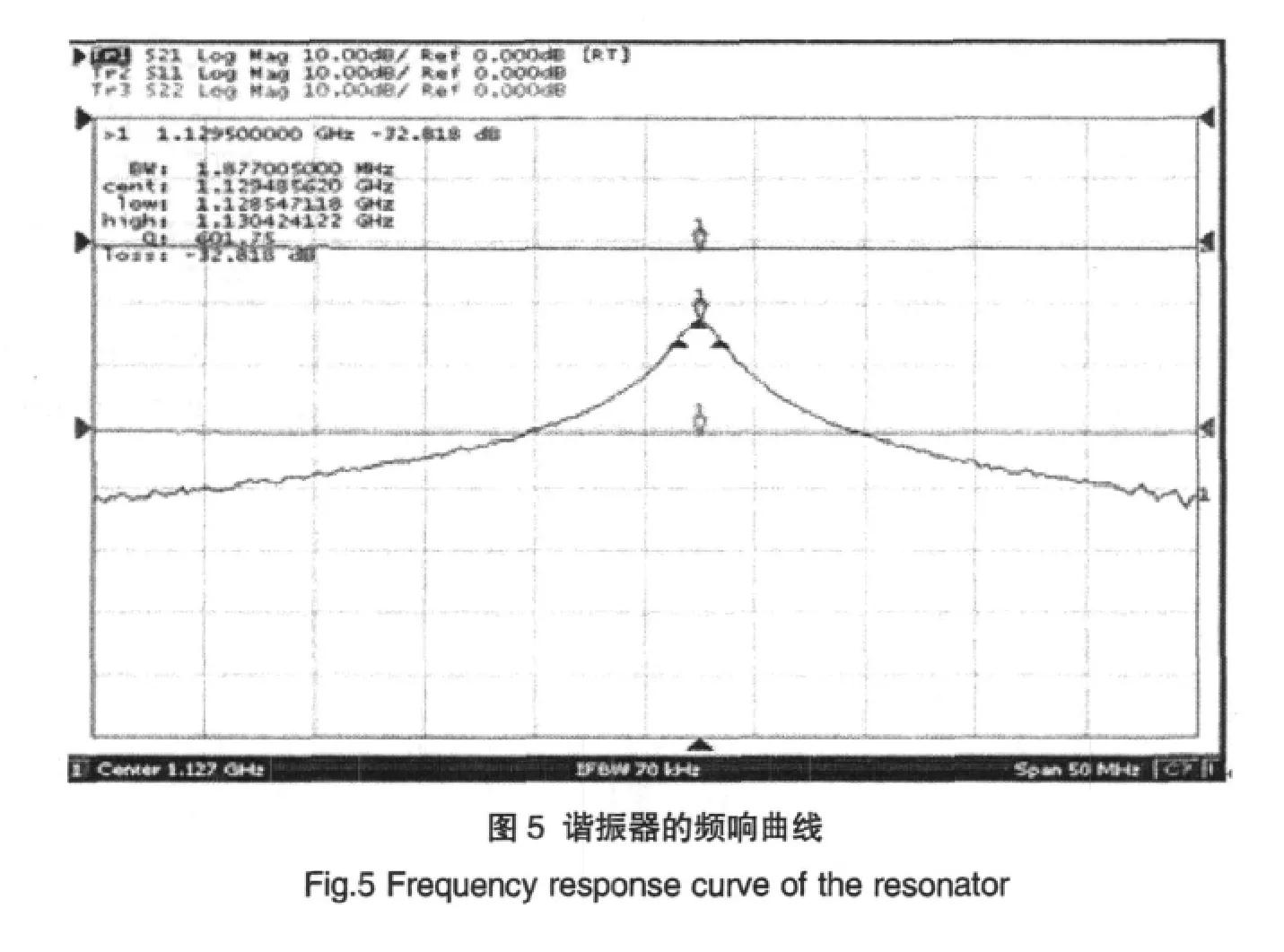
选取介电常数为74的BaO-TiO2-Sm2O3系统的微波介质材料制作介质同轴谐振器。按照电子陶瓷的生产工艺配制瓷料，然后加入7wt.%左右的PVA粘合剂进行造粒，采用干压成型，压力为20MPa压制出内外径分别为3mm和10mm，高度9.5 mm的圆柱形生坯，在1350℃温度下烧结2h，产品的内外径分别是2.5mm和8mm，高度8.3 mm的瓷柱，然后在除一个端面外的所有内外表面涂覆银浆，在880℃下烧渗银。将谐振器的开路端加载高Q值的电容,分别与网络分析仪的输入输出端口耦合，用E5071B网络分析仪测量回路的传输特性，从曲线直接读出传输型谐振器的谐振频率和有载Q值。测试曲线如图5所示。

为了分析电容的容量和Q值对试验结果的影响，选择2种不同类型的电容，每种电容选取不同的容量，分别加载在同一规格的同轴谐振器的开路端，从网络分析仪上读出谐振频率和Q值。数据列于表1中。表中固定电容一栏“×2”表示输入输出电容相等，只有一个电容值表示输入电容为固定电容，输出电容为间隙电容(间隙为2mm)；表中的分布电容是指在厚为1mm,宽2.5mm的三氧化二铝(A12O3)基片上的三个导电带之间形成的间隙电容,其电容的大小与间隙成反比。

从表1可以粗略看出，加载的电容越小，QL值越大，插入损耗越小，谐振频率偏高。从计算出的Qu值可知，用固定电容耦合的谐振器的QU很小，而用分布电容耦合的谐振器Qu的很大，两者相差一倍，这是因为公式（10）是在假设电容具有较高的Q值的情况推导出来的，而0805型电容器的Q值比较小。也就是说当耦合电容的损耗较大时，不能用公式（10）来计算谐振器的无载Q值。用分布电容耦合时，随着电容量的进一步减小（即间隙逐渐增大），谐振频率的测量值差距越来越小，计算的Qu值也越来越接近，这种情况用上述公式（10）和（12）很容易解释。这是因为公式（12）的C01很小时，C01／C1也很小，插入损耗IL也很小，（10）式分母的指数值也很小。因此，当耦合电容的Q值较高时，它与网络分析仪两端口耦合越弱时，用传输法测量的谐振频率和Q值越接近谐振器本身的值（指反射法测量的值），甚至用测量值代替“真值”（实际上也是测量值）所产生的误差不超过1%。

从表1中加载不对称电容所得的数据对由介质同轴谐振器构成滤波器的调试有很大的指导意义，即增大输入电容（或输出电容）可以改变滤波器的通带带宽。

表1测试数据Tab.1 Measurement data

4 结论

（1）在1/4波长介质同轴谐振器的开路端加载高Q值的对称电容与网络分析器的两端进行弱耦合，用网络分析仪测量其传输曲线，从曲线上直接读出回路谐振频率、有载Q值及插入耗损，然后利用上述公式（10）和（12）能计算得到谐振器本身的谐振频率和无载Q值。

（2）当加载的电容的Q值越高、耦合电容量越小，插入损耗越小（小于-30dB），测量的有载Q值越接近谐振器的无载Q值；但当加载加容的Q值较低、电容量越大时，则测量的有载Q值越小，离谐振器的无载Q值越远。当耦合电容的损耗很小，耦合非常弱时，用测量值代替真值所产生的误差将很小。

（3）在谐振器的开路端加载电容时，谐振器的谐振频率降低，可用（6）式计算，对由电容耦合的介质滤波器的设计和制作有一定的指导作用。该方法适用于介质陶瓷谐振器的自动测量和分选，对大批量生产来说非常实用。

1曹良足,黎泽仁,范跃农等.介质同轴谐振器的结构与测量.中国陶瓷,2005,41（2）:31～33

2 ChuaL H and SyahkalD M.Accurateand direct characterization ofhigh-Q microwave resonatorsusing one-port measurement.IEEE Trans.Microwave Theory and Tech.,2003,51(3):978～985

3 Raymond S.Kwork and Ji-Fuh Liang.Characterization of high-Q resonators for microwave filter applications.IEEE Trans.Microwave Theory and Tech.,1999,47(1):111～114

4曹良足,孙敏松.串联谐振法测量1/4波长介质同轴谐振器的特性参数.电子测量技术,2007,30（10）:64～66

5顾继慧.微波技术.北京:科学出版社,2004,2

6甘本跋,吴万春.现代微波滤波器的结构与设计.北京:科学出版社,1973

7倪尔瑚.介质谐振器的微波测量.北京:科学出版社,2006

8中国矿业学院数学教研室.数学手册（第二版）.北京:科学出版社,1980,9

Abstract

A method for measuring the properties of TEM type dielectric resonators was described.Two high-Q capacitors were connected to the open end of a resonator,and the resonator was weakly coupled to a Network Analyzer through these capacitors.The transmission curve was measured by the Network Analyzer,the circuit frequency and the loaded Q value of the resonator could be read from the curve.The differences between the theoretical and measured values have been analyzed theoretically,the formula for calculating the resonant frequency and the unloaded Q value of the resonator were derived.The dielectric ceramic resonators were made of BaO-TiO2-Sm2O3microwave dielectric material with the dielectric constant being 74.Compared with the reflection measurement,the calculated value is more accurate.

Keywords dielectric ceramic resonator,resonant frequency,unloaded Q value

Received on May.13,2010

Cao Liangzu,E-mail:clz4233@yahoo.com.cn

MEASUREMENT OF THE PROPERTIES OF DIELECTRIC CERAMIC RESONATORS

Cao Liangzu Guo Tongjun
(School of Mechanical and Electronic Engineering,Jingdezhen Ceramic Institute,Jingdezhen Jiangxi 33403,China)

TQ174.75

A

1000-2278（2010）04-0581-05

2010-05-13

江西省教育厅科研项目（编号：GJJ10564）

曹良足，E-mail:clz4233@yahoo.com.cn