电气化铁道牵引网谐波电流放大仿真分析

王 奇

0 引言

目前，晶闸管相控整流技术及PWM控制技术在电力机车中的广泛应用，使电气化铁道中存在大量而丰富的谐波电流，因此，电力牵引负荷谐波已经成为电力系统的主要谐波源之一。当谐波源在谐波频率下激励一个感抗和容抗大小近似相等的电路时，将使得该电路发生谐波谐振。谐波谐振是电力系统中的一种较为常见的现象，发生谐振时会产生过电压和过电流，危及系统稳定运行。谐波谐振引起的过电压将造成高压电气设备绝缘损坏，导致氧化锌避雷器损坏，造成测量仪表误差，引起保护装置误动，增大电网谐波损耗等一系列危害[1～2]。

目前对于电力系统谐波谐振的研究已经取得了一些成果[3～5]，而对于牵引供电系统的谐波谐振研究甚少[6]，本文在电力系统谐波谐振的研究成果基础上，从理论推导和仿真实验2个方面对牵引供电系统谐波谐振进行了深入研究，对牵引网中的谐波电流放大进行了分析。

1 牵引供电系统谐波电流放大

当电力机车向牵引网注入谐波电流时，某些次数的谐波电流将会激励牵引网发生谐振，谐波电流放大即为谐振的一种表现形式，它将引起牵引网设备的绝缘损坏以及保护误动等问题。图1 a为牵引供电系统原理图，其等值电路如图1 b所示[7]，牵引网总长为L。

从图1 b可以得到下列等式：

式中，It为机车电流；I1、I2分别为流向牵引变电所(SS)方向和分区所(SP)方向的牵引网电流；Z1、Z2分别为在机车位置向牵引变电所方向和分区所方向看去的牵引网阻抗。

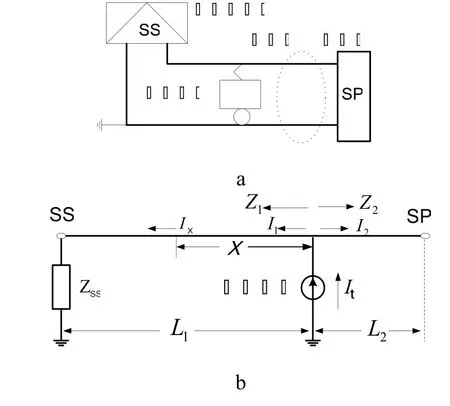
图1 牵引供电系统及其等值电路图

利用电力输电线路无源双端口网络的等值电路原理（见图2[8]），可以得到双端口网络方程式（4）和式（5）。

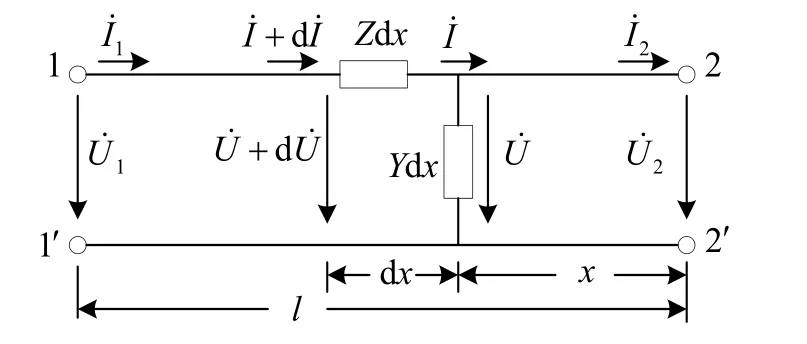
图2 双端口网络等值电路图

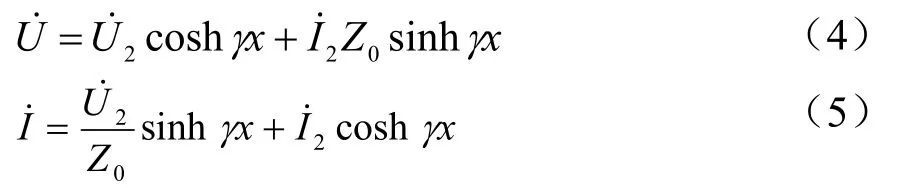
在机车处向牵引变电所方向看去以及向分区所方向看去，分别运用双端口网络方程即可求得Z1、Z2。

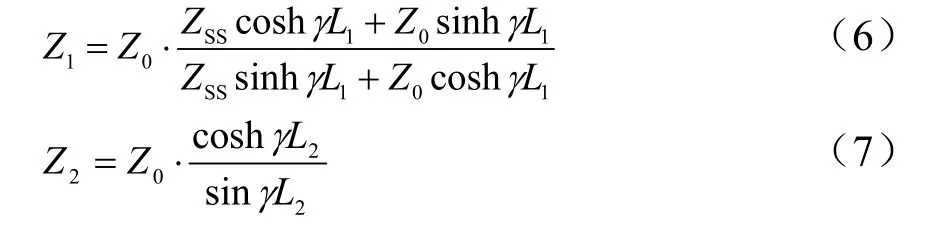
（计算中分区所处做断路处理即端口电流为零）

机车电流源相对整个牵引网的阻抗为上述阻抗并联，即

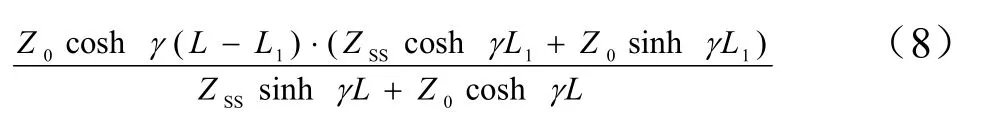
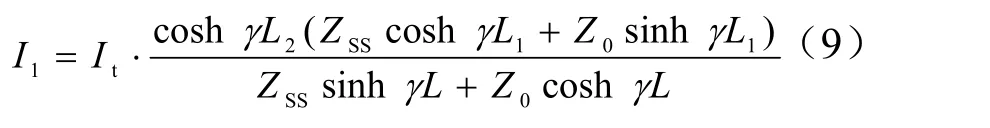
由式（2）可得

再次应用双端口网络方程可以得到距机车X处（SS方向）的牵引网电流

牵引网电流放大倍数KX=IX/I1，其表达式如下

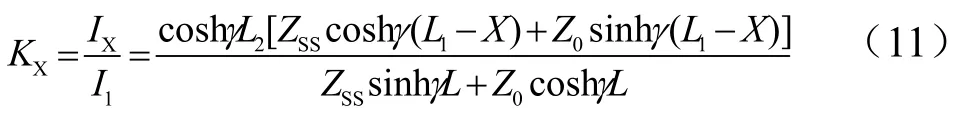
当机车位于牵引网末端时，即L2= 0、L1=L，牵引变电所处的谐波电流放大倍数

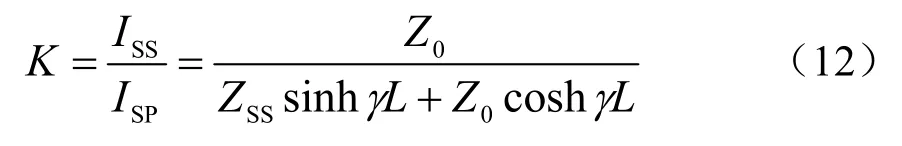
从以上表达式可以看出，影响牵引供电系统谐波谐振点的主要因素有牵引网的单位长阻抗和导纳、牵引网长度、机车位置、牵引变电所等值阻抗，当机车向牵引网注入的谐波频率等于或接近牵引网谐振点时就可能引起系统谐振。

2 谐波电流放大仿真分析

2.1 系统参数

系统参数为某AT供电方式的电气化铁道典型数据，数值分别如下，牵引变电所及系统等值阻抗ZSS= 1.180 + j9.750（Ω）；牵引网单位长阻抗ZC=0.119 + j0.752（Ω/km）；牵引网单位长导纳YC=j2.337 8×10-6（S/km）。

2.2 牵引供电系统谐波电流放大仿真分析

当牵引网长度分别为10，20，30，40和50 km时，机车位于牵引网末端，这时机车向牵引网注入的谐波电流在牵引网首端即牵引变电所处引起的谐波电流放大情况如图3所示。

从图中可以看出牵引网长度越长，机车谐波电流在牵引网首端引起的谐波电流放大的谐波次数越低。牵引网长度与谐波电流放大时的谐波次数关系如表1所示。

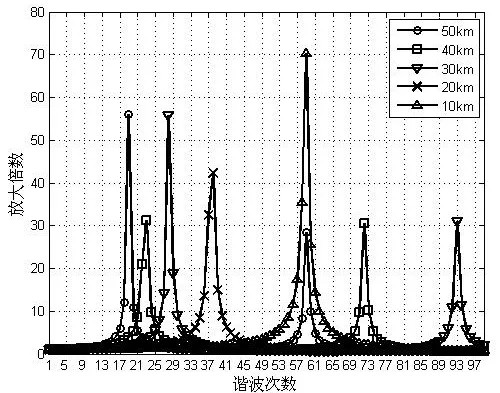
图3 不同长度牵引网的谐波电流放大图

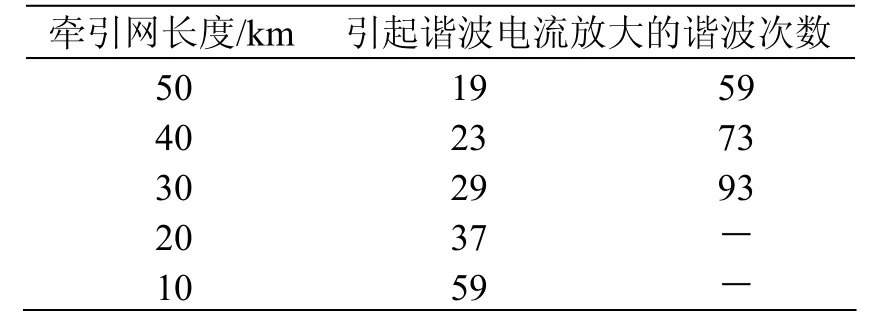
表1 不同长度牵引网谐波电流放大时谐波次数表

当牵引网长40 km，机车分别位于40，30，20和10 km处时，机车注入的谐波电流在牵引网首端引起的谐波放大情况如图4所示。

图4 40 km牵引网的谐波电流放大图

由图4可以得到，当机车位于牵引网的不同位置时，其在牵引网首端引起谐波电流放大的谐波次数基本固定，但其引起谐波电流放大的倍数会随着其位置的变化而改变，距离牵引变电所越近放大倍数越低。

下面分3种情况讨论牵引网长度、机车位置以及距离机车不同位置处的谐波电流放大情况。

牵引网长为50 km，机车位于牵引网末端，在距离机车10，20，30，40和50 km的牵引网处引起的谐波电流放大情况如图5所示。从图中可以看出，当机车位置确定后，其在牵引网的不同位置引起谐波电流放大时的谐波次数不发生变化，仅谐波电流放大倍数变化，并且此时发生谐波电流放大的谐波次数主要集中在19次和59次。

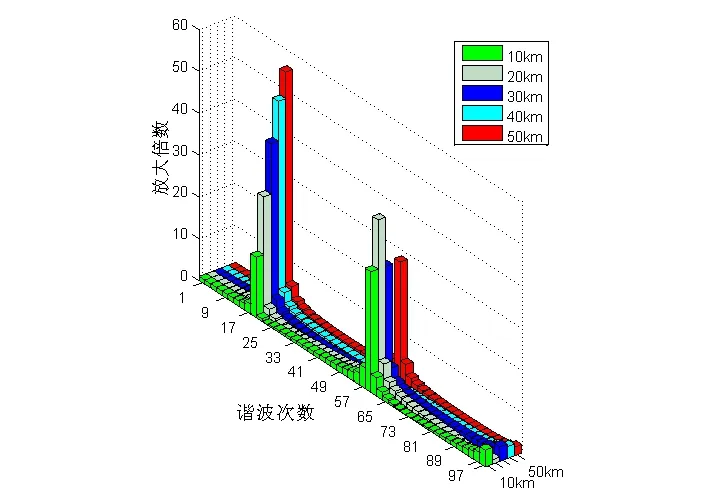
图5 机车位于牵引网末端时牵引网不同位置处的谐波电流放大图

不改变牵引网长度，而机车位于30 km处，在距离机车10，20和30 km的牵引网处引起的谐波电流放大情况如图6所示。其发生谐波电流放大时的谐波次数主要集中在19次。

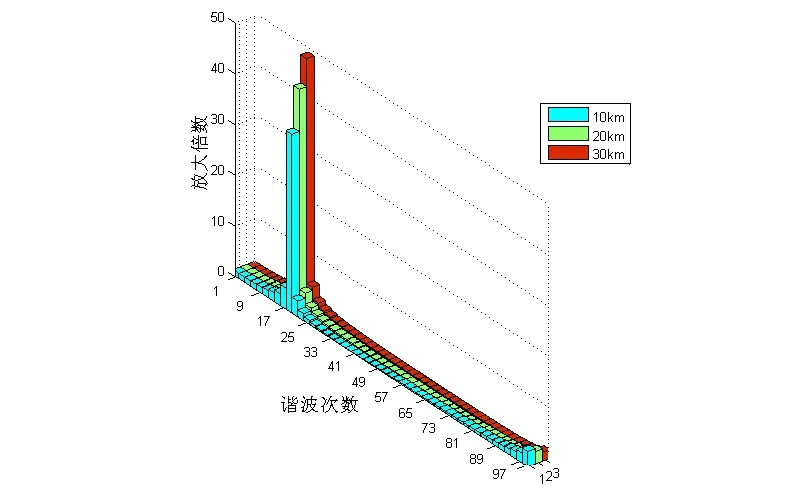
图6 机车位于30 km时牵引网不同位置处的谐波电流放大图

当牵引网长度为30 km，机车位于牵引网末端，在距离机车10，20和30 km的牵引网处引起的谐波电流放大情况见图7。可以看出此时发生谐波电流放大时的谐波次数主要集中在29次和93次。

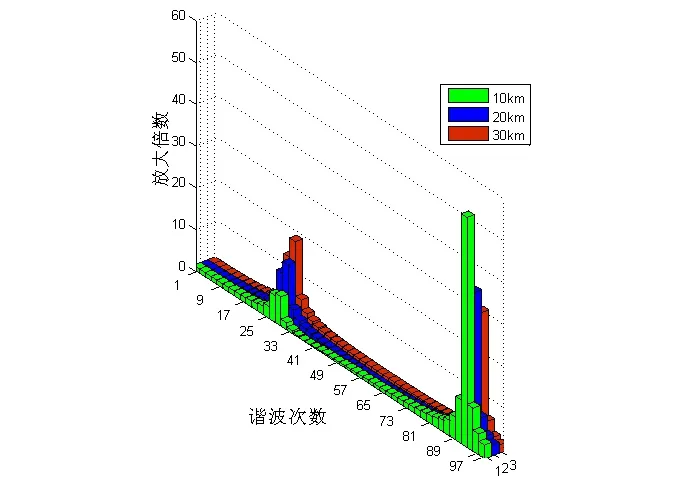
图7 机车位于牵引网末端时牵引网不同位置处的谐波电流放大图

2.3 基于PSCAD/EMTDC的仿真比较

为了与上述理论分析结果进行对比，本文利用PSCAD/EMTDC软件搭建了50 km长的单相牵引网模型，并采用传输线的П模型级联实现牵引网的等效，分别在牵引网末端以及30 km处向牵引网注入谐波电流，得到如图8和图9的仿真结果。

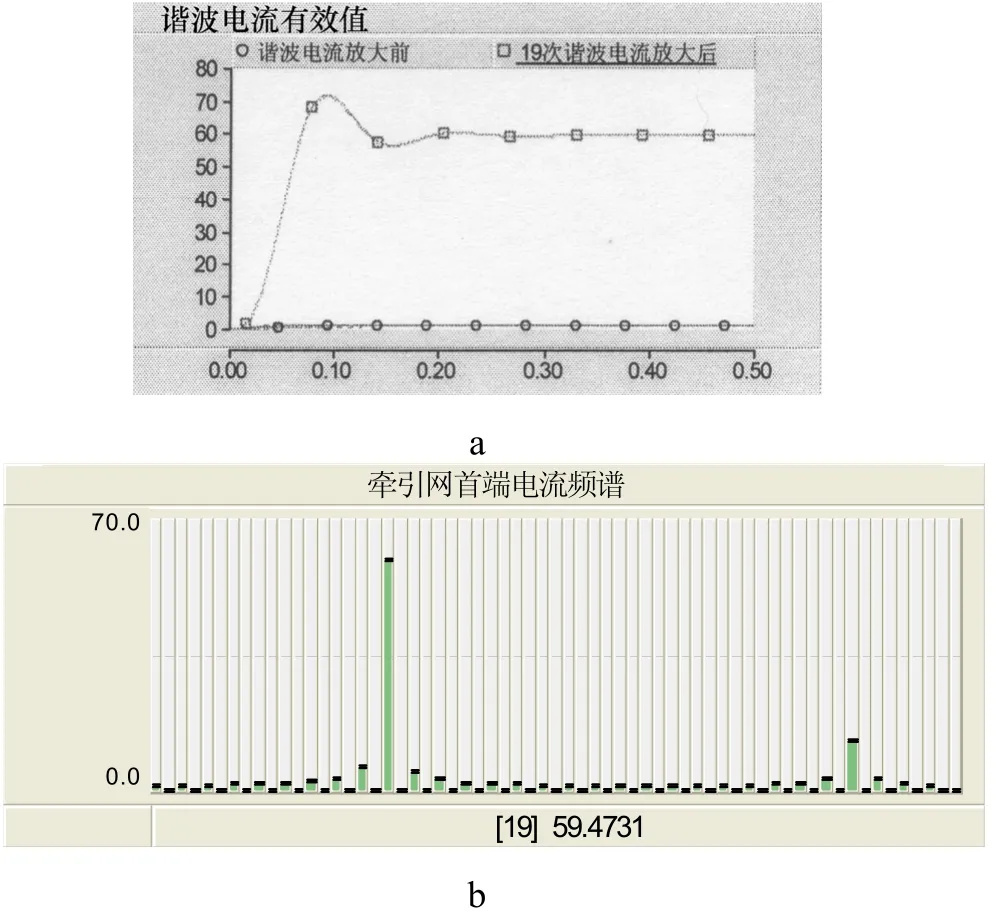
图8 机车在牵引网末端时的谐波电流仿真图

从图8 a中可以看到在牵引网首端，19次谐波电流发生了明显的放大现象，19次谐波电流有效值放大近60倍，图8中的仿真结果与图5分析基本吻合。

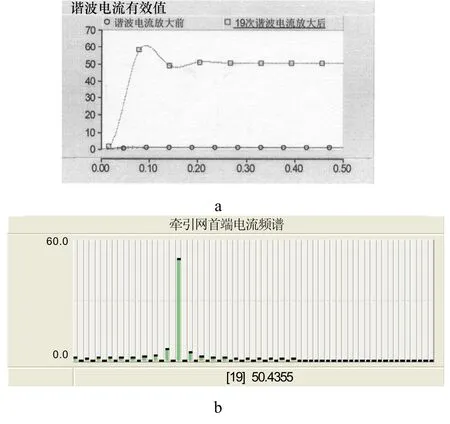
图9 机车在牵引网30 km处时的谐波电流仿真图

由图9 a中可以看出当机车位于牵引网30 km处时，在牵引网首端引起谐波电流放大的谐波次数仍然为19次，其有效值放大约50倍，图9的仿真结果与图6分析一致。

3 结束语

本文通过理论推导以及仿真实验对牵引供电系统中发生谐波电流放大的各种情况进行了深入分析，得出了牵引网长度、机车位置以及牵引网的不同位置处等因素与发生谐波电流放大的关系。牵引网长度越长引起谐波电流放大的谐波次数越低；机车位置固定后，其引起牵引网不同位置处发生谐波电流放大时的谐波次数固定；牵引网长度固定后，机车在牵引网的不同位置时引起牵引网首端谐波谐振时的谐波次数固定。本文所提出的仿真分析方法将对牵引供电系统的谐波电流放大以及谐波谐振现象研究提供理论依据和参考。

[1]史呈逵.电网电容器组谐波谐振和谐波放大的研究[J].电力自动化设备，2001，21(7)：63-38.

[2]董国震，和敬涵.电力系统局部电路谐波谐振产生原因分析及对策[J].继电器，2007，35（1）：77-80.

[3]徐文远，张大海.基于模态分析的谐波谐振评估方法[J].中国电机工程学报.2005，25（22）：89-93.

[4]周辉，吴耀武，娄素华，等.基于模态分析和虚拟支路法的串联谐波谐振分析[J].中国电机工程学报.2007，27（28）：84-89.

[5]M.Z.C.Wanik,Y.Yusuf,S.N.Al-Yousif, et al.Simulation of Harmonic Resonance Phenomena in Industrial Distribution System[C].TENCON 2004.2004 IEEE Region 10 Conference Nov.2004.

[6]Kadhim Rafat, Kelsey Dominic.25 kV Harmonic Resonance Modelling on the Channel Tunnel Rail Link.The Institution of Engineering and Technoloy Seminar on EMC in Railway, 2006.

[7]Hanmin Lee,Changmu Lee,Gilsoo Jang, et al.Harmonic Analysis of the Korean High-Speed Railway Using the Eight-Port Representation Model[J].IEEE Transactions on Power Delivery, 2006,21(2).

[8]韩祯祥.电力系统分析[M].杭州：浙江大学出版社，1997.