光测轨检系统的高精度摄像机标定*

傅勤毅,刘姣姣,邱志强,马 广

(1.中南大学交通运输工程学院,湖南长沙 410075;2.中国人民解放军 76321部队,广东广州 510500;3.中南大学土木建筑学院,湖南长沙 410075)

便携式轨检仪是检查轨道病害,指导线路维修,保障行车安全的动态检测设备,在线路检查、安全监控等方面发挥日益突出的作用。随着数字图像处理技术、数字摄像机、计算机等信息处理技术的飞速发展,采用基于光测法,以高速图像处理技术取代光电技术的的轨检技术[1]成为发展趋势。传统的轨道检测系统主要采用光电技术,利用传感器融合技术进行轨道检测,系统造价高。多传感器系统结构复杂难以适应高精度实时测量要求。本文采用光测图像技术取代传统方法进行轨道检测。只需 1对 CCD摄像机进行数据采集,从而大大节省了成本,且运算速度快,能满足轨道高精度实时测量的要求。

1 光测轨检系统构建方案

1.1 系统方案

在轨检仪上架设 1对 CCD摄像机,形成双目视觉测量系统[2]。测量时,2个摄像机同时对靶标进行拍摄得到成对图像,由图像处理的信息计算出轨道横向变形量。系统方案原理图见图 1。

图 1 光测轨检系统方案Fig.1System solution of track inspection

图 1中:立方体 V为轨检仪,C1C2为转向架上的检测梁,在 C1C2两端安装 2台 CCD数字摄像机,车内适当位置安装车载主控计算机及配套通讯系统,在靶杆上端和中部位置设置 2个标志点 Pa和Pb。轨检仪测量开始前,采用标准控制板标定 2台摄像机,获得精确的摄像机内外参数和像差模型,从而建立精确的摄像机几何成像模型。轨检车在运行过程中,2台摄像机连续跟踪靶杆标志点 Pa和Pb,记录靶杆图像,并实时传输到主控计算机。主控计算机对图像进行自动分析和数据处理,获得 C1C2与PaPb之间的距离D作为该点轨线变形量。如果靶杆 L在图像中的轮廓线清晰,亦可不设置附加标志点 Pa和 Pb,在图像处理中直接以 L为分析对象,计算出 C1C2和L之间的距离作为该点轨线变形量。

1.2 镜头畸变模型

理想的透镜成像是针孔模型,物点和像点满足相似三角形关系。实际上,相机由于加工、工艺、组装等方面的原因,会导致非线性畸变[3],主要有几个方面:径向畸变,偏心畸变,薄棱镜畸变。这些畸变量同作用引起图像变形。畸变图见图 2。

图2 畸变图Fig.2 Diagram of distortion

理想的透镜成像模型时,理论像点位置 A,经过径向畸变和切向畸变后位于 A'。选择畸变模型[4]:

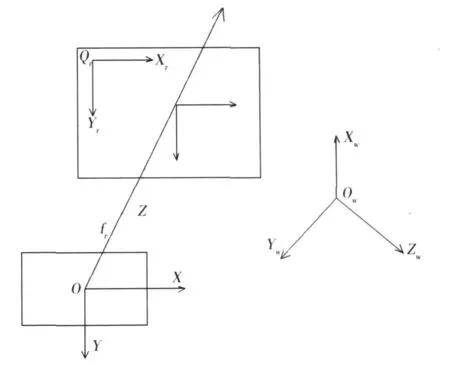
图3 像面与靶标面坐标变换Fig.3Coordinate transformation between imaging plane and drone plane

其中:k1和 k2为径向即畸变系数;p1和p2为切向畸变系数;s1和s2为薄棱镜畸变系数(忽略不计)。

2 基于辅助面的摄像机标定方法

2.1 建立靶标面与像平面的对应透视关系

首先在二维平面靶标上建立坐标系,设为辅助平面,建立包含摄像机畸变的数学模型,确定平面靶标与摄像机成像面的坐标对应关系。而后将空间点世界坐标系坐标与成像面的数学关系先转换到世界坐标系与靶标辅助平面坐标系的数学关系,再转换回与成像面的坐标系数学关系。

标定时只需知道空间特征点是怎样变换到图像这一变换关系即可,因此,采用双平面隐式模型将摄像机参数组合成中间参数,只需解线性方程就可以标定摄像机,简化了标定方法[4]。

理想成像模型中实际像面坐标系 Oxy,靶标平面坐标系 Orxryr,像面与辅助平面理想透视模型为:

选择畸变模型:

改写理想透视模型为畸变透视模型:

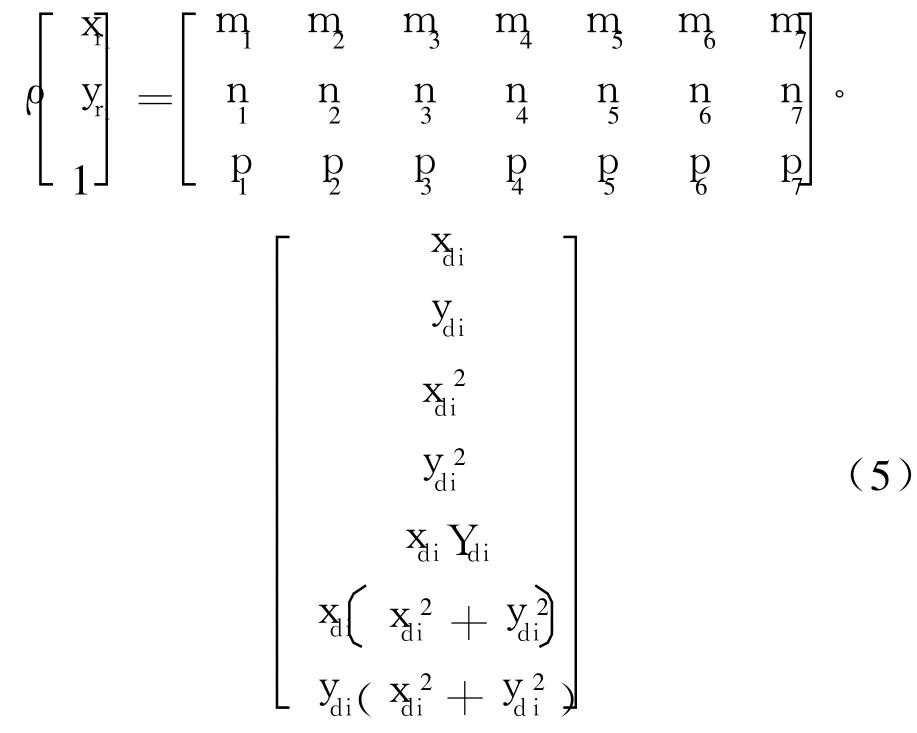
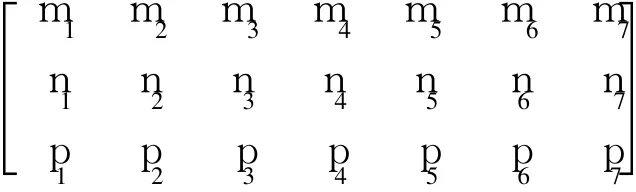
2.2 建立空间坐标系与辅助平面坐标系的透视关系

平面坐标系与世界坐标系为旋转、平移关系,辅助平面坐标系同像面坐标系在搭建视觉系统[5]时设定为平移关系。辅助平面与像面构成理想成像系统,fr为有效焦距,满足理想透视变换模型,有:

世界坐标系与像面坐标系满足数学模型:

代入式(6),得:

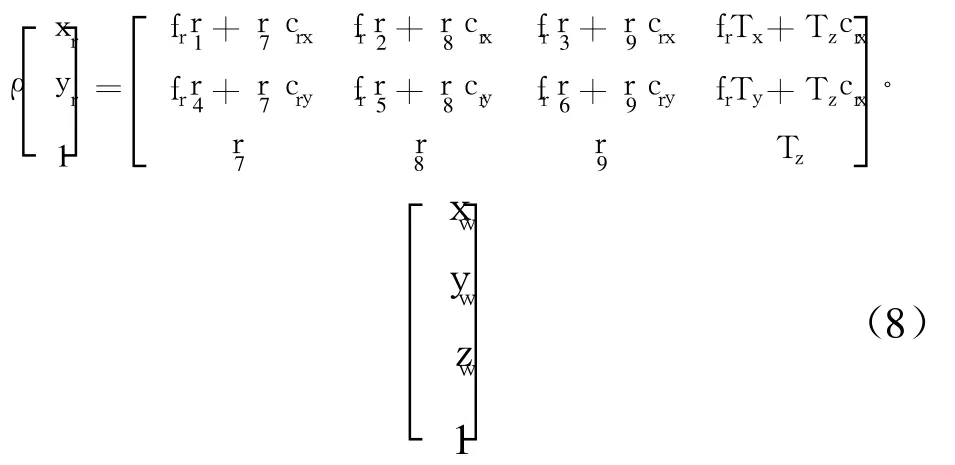
辅助平面坐系与像面坐标系满足平移关系,则有:

代入式(8)得到:

3 标定试验及数据处理

3.1 标定实验方案设计

3.1.1 选用高精度标定模板

选择一款 76系列高精度标定模板[6]。外型尺寸为 76×76;精度指标为 +/-0.015 mm;图案为实心圆阵列 11×11;图案规格:圆直径为 3 mm,点距为 5 mm。在模板图上建立坐标系(取标定板上 0号特征点为原点,水平方向为 xr轴,竖直方向为 yr轴,用万能工具显微镜可以精确测定板上其他特征点的坐标。标定时,双摄像机同时从不同角度拍摄得到一组图像即可。实现简单方便。图中小圆圆心用于标定,不规则分布的大圆用于其他标定圆的位置识别。

图4 标定模板Fig.4 Calibration plate

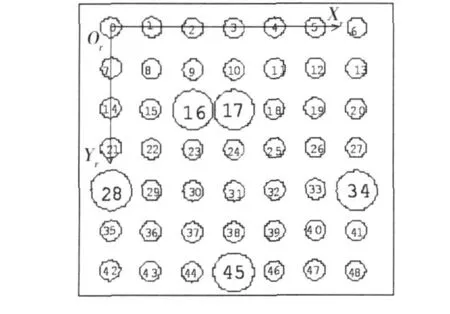
图5 特征圆编号Fig.5 Mark the roundness

3.1.2 选择摄像机和镜头

测量过程需动 /静态拍摄,根据测量的靶标大小、精度要求、现场环境(温度、湿度、干扰、光照条件等)选择一款高性能工业检测专用数字工业摄像机即 MV-USBⅡ系列彩色 /黑白数字工业摄像机,具有高分辨率、高精度、高清晰度、低噪声等特点。依据 CCD制式、接口、芯片尺寸选择型号为 VS-M1023的工业连续变倍显微镜头。其尺寸规格和焦距等各项性能满足精度要求。

3.2 标定数据处理及误差分析

双摄像机同时从不同角度拍摄一个靶标的几组图像得到的标定图像,得到标定特征圆圆心的像面坐标,对应辅助面坐标。

将数据代入式(5)得

对 F(x)求导,找平稳点,得x=(ATA)-1ATb为整体极小值。其中:要求 ATA非其次。

该标定试验中:

线性最小二乘优化公式求 x,

标定前已知参考面坐标系与世界坐标系位置关系如下:r1=0.478 6,r2=-0.862 5,r3=-0.069 4,r4=0.872 5,r5=0.488 8,r6=0.151 0,r7=-0.100 1,r8=0.132 9,r9=0.986 2,tx=1 772.213,ty=6.012,tz=1 040.936。 (17)

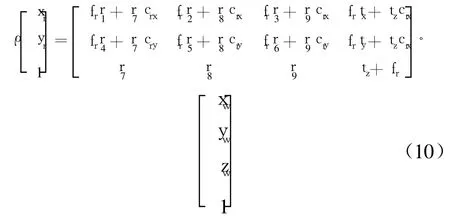
将 r1～r9,tx,ty和 tz代入式(10),用线性最小二乘法,解出 fr,crx和 cry。

3.3 标定实验结果及误差分析

采用空间点再投影法测定误差[7]。将空间三维点按照标定得到模型再投影到像面上,得到实际像面坐标之间的平均误差、方差、标准偏差衡量。为了保证该标定方法的准确度和稳定性,进行 5次独立标定。单个摄像机标定结果误差见表 1。

表1 标定实验结果

实验数据表明:多次独立标定最大误差均在一个像素以内,达到了亚像素标准,精度较高。使用标定模板提高图像的鲁棒性及圆特称提取精度,且解线性方程组,算法计算速度较快,实用性强,达到了预期目的。

4 结 论

传统的 RAC标定法进行摄像机标定只考虑径向畸变,且对摄像机的位置有约束。本文采用双平面进行标定,以靶标作为辅助面分两步标定。选用的摄像机畸变模型同时考虑径向畸变和切向畸变,提高了标定精度;采用最小二乘法计算高精度成像隐式模型简单快速。选用一种易于制作和携带的具有不同大小圆形特征点的平面标定模板,在无需控制任何运动参数的情况下,测量系统对该标定板在不同角度拍摄一组图像,通过设计稳定可靠标定算法,方便、快速、稳定地实现双目立体测量系统的现场标定,较传统的标定方法具有约束条件少、操作简单、精度高等优点。多次试验数据显示平均误差、最大误差均在 1个像素内,标定结果较理想。该标定法在光测轨检系统应用中效果良好,可以达到高精度快速实时测量的要求。

[1]张广军.机器视觉[M].北京:科学出版社,2005.ZHANG Guang-jun.Machine vision[M].Beijing:Science Press,2005.

[2]马颂德,张正友.计算机视觉——计算机理论与算法基础[M].北京:科学出版社,1998.MA Song-de,ZHANG Zheng-you.Computer vision:Theory and application[M].Beijing:Science Press,1998.

[3]谭晓波.摄像机标定及相关技术研究[D].长沙:国防科技大学,2004.TANG Xiao-bo.Research about calibration and technology related[D].Changsha:National University of Defense Technology,2004.

[4]朱铮涛,黎绍发.镜头畸变及其校正技术[J].光学技术,2005(1):136-138.ZHU Zheng-tao,LI Zhao-Fa.Lens distortion and revise technology[J].Optical Technology,2005(1):136-138.

[5]胡 勇,王从军,黄树槐.双目视觉传感器的自动标定[J].武汉理工大学学报,2005,27(10):67-69.HU Yong,WANG Cong-jun,HUANG Shu-huai.Calibration automation of the binocular stereo vision sensor[J].Journal of Wuhan University of Technology,2005,27(10):67-69.

[6]Grosky W I,Tamburino L A.A unified approach to the linear camera calibration problem[J].IEEE Trans on PAMI2,1990,12:6632-6711.

[7]Salvi J,A rmangue X,Bat lle J.A comparat ive review of camera calibrat ing methods w ith accuracy evaluat ion[J].Pat tern Recognit ion,2002,35(7):1617-1635.

[8]Eian J,Poppele R E.A single2camera method forth ree 2 dimensional video imaging[J].Journal of Neuro Science Methods,2002,120(1):65-83.