基于MRAS和SVPWM的无速度传感器永磁同步电动机控制研究*
上海电力学院(上海200090) 梅柏杉 程晓勇 刘 斌
蔚县空中草原风厂(河北 075000) 刘玉刚
1 引言
永磁同步电机因其功率密度大,效率高的优点,在国防、工农业生产和日常生活等方面获得越来越广泛的应用。由于无速度传感器不仅可以降低成本,还可以增强系统稳定性,所以无速度传感器永磁同步电机的矢量控制方法,也成为研究中的一个热点[1]。模型参考自适应(MRAS)是一种较常用的估算转子位置和速度的方法。模型参考自适应辨识的主要思想是将含有待估计参数的方程作为可调模型,将不含未知参数的方程作为参考模型,两个模型具有相同物理意义的
输出量。两个模型同时工作,并利用其输出量的差值根据合适的自适应率来实时调节可调模型的参数,以达到控制对象的输出跟踪参考模型的目的[2]。根据稳定性原理得到速度估计自适应公式,系统和速度的渐进收敛性由Popov的超稳定性来保证。
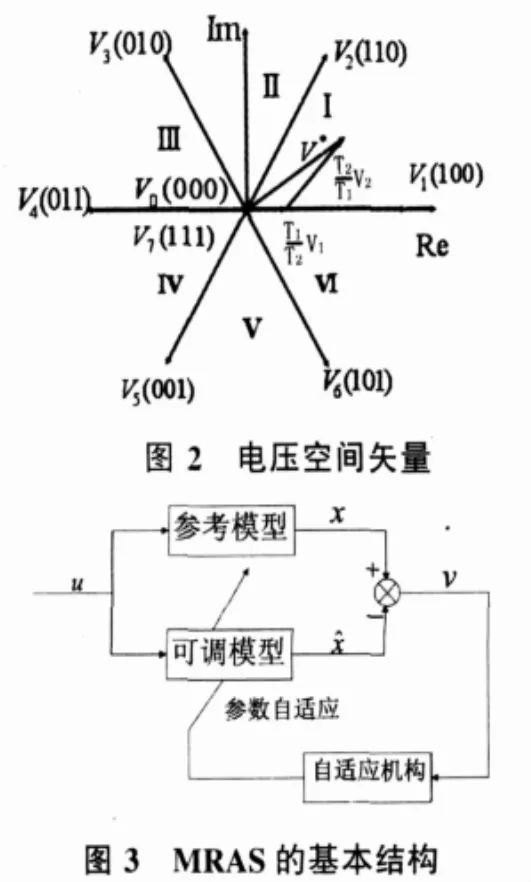
近年来,电机的空间矢量理论被引入电机控制系统中,形成了空间矢量脉宽调制技术(SVPWM)。其原理就是利用逆变器各桥臂开关控制信号的不同组合,使逆变器的输出空间电压的矢量运行轨迹尽可能接近圆形[3]。SVPWM能够明显地减小逆变器输出电压的谐波成分,降低转矩脉动,而且有较高的电压利用率,更易于数字实现,应用前景十分看好。
2 永磁电机的数学模型及矢量控制
PMSM把永磁体作为转子,三相 A,B,C对称绕组作为定子,在定子三相绕组中通以相位相差120°的三相交流电,产生旋转的定子磁场,该磁场与永磁体励磁场相互作用产生电磁转矩。假设PMSM磁路为线性,忽略铁心损耗,所有绕组产生的磁动势波和磁场在空间都按正弦分布[4]。经过推导后可以得到PMSM在dq坐标系下的数学模型如下:

矢量控制实际上是对电动机定子电压或电流矢量的相位和幅值同时进行控制。对于贴面式PMSM,Ld=Lq。一般,为了简化控制策略,采用 id=0,将此式代入电磁转矩方程式(3),可得电磁转矩方程为:

即电磁转矩只和q轴的电流 iq有关,所以在贴面式永磁同步电机的矢量控制系统中,令 id=0时,通过控制 iq,即可实现电磁转矩的解耦控制。图1所示为采用 id=0策略的矢量控制框图。
通常转子实际位置是通过编码盘或测速发电机等位置传感器获取的。本文采用模型参考自适应状态观测器估算转子角度和转速,实现PMSM的无速度传感器矢量控制。
3 空间矢量PWM

空间矢量PWM(SVPWM)控制策略采用逆变器空间电压矢量的切换以获得准圆形旋转磁场,从而在不高的开关频率时,提高了电压型逆变器的电压利用率和电机的动态响应性能,同时还减小了电机的转矩脉动等[5]。其关键在于SVPWM更加直接地控制了交流电机的旋转磁场。
对于三相电压型逆变器电路,每相桥臂可以看作是一个开关S,开关函数 SU(t)、SV(t)、SW(t)表示三个桥臂的开关状态。对于两电平SVPWM逆变器,这些开关函数在任意时刻的取值为1或0。其中1表示该开关接通正电位,0表示接通负电位。根据开关函数取值的不同组合,逆变器最多有23=8种工作状态。相应的逆变器输出电压空间矢量可表示为

其中,Vdc为变频器中间直流电压值,a=ej120°。
对于任意给定的空间电压矢量,都可以由这8个三相空间电压矢量合成。利用它们的线性组合,构成一组等幅而不等相位的电压空间矢量,从而形成尽可能逼近圆形的旋转磁场。由于它间接控制了电机的旋转磁场,所以也可称作磁链跟踪控制的PWM逆变器。
! 模型参考自适应系统
MARS的主要思想是将含有待估计参数的方程作为可调模型,将不含未知参数的方程作为参考模型,两个模型具有相同物理意义的输出量。两个模型同时工作,并利用其输出量的差值,根据合适的自适应率来实时调节可调模型的参数,以达到控制对象的输出跟踪参考模型的目的[6]。根据稳定性原理得到速度估计自适应公式,系统和速度的渐近收敛性由Popov的超稳定性来保证。
根据所得电机数学模型,可以看出电流模型与电机的转速有关,因此可选PMSM本身作为参考模型,而电流模型为可调模型,采用并联型结构辨识转速。
PMSM在dq轴下的定子电流数学模型为

为便于分析系统稳定性,应使转速量被约束于系统矩阵A中,因此对控制量和状态变量作相应变换,得

其中并联可调模型中 ω是需要辨识的量,而其它参数不变化。状态变量误差

首先将并联模型状态方程改写为以下形式

取 D=I,则 v=Ie=e。
根据Popov超稳定性定理,如果满足:
1)传递阵 H(s)=D(sI-A)-1为严格正实矩阵;
2)η(0,t0)= ∫0t0vTwdt≥ - γ0,∀t0≥0,γ0为任一有限正数。
可得辨识算法为

其中,k1,k2≥0,将式(8)代入式(14)可得



?
5 仿真和结果
如下图4基于MARS永磁同步电机无速度传感器SVPWM仿真系统图。
速度环PI参数取Ki1=0.5,Kp1=1;电流环Ki2=10,Kp2=1。模型参考自适应系统中,PI调节中经过调试确定下来 Ki=100、Kp=0.001,可以得到对转速的估计值。
仿真中使用的永磁同步电机参数见表1。
负载转矩 T为2N·m,在0.3秒加负载扰动为3.5N·m,仿真结果如下:
由图5和图6可知,模型自适应速度观测系统能够准确观测转子位置和转速,具有较好的抗扰动能力,但是MRAS辨识过程具有一定的时间延迟,并且在低速状态下会出现小的波动,这也是模型参考自适应系统还有待解决的问题。


6 结论
本文将模型参考自适应观测器和空间矢量脉宽调制技术应用于永磁同步电机无速度传感器矢量控制中。根据永磁同步电机的数学模型,设计了一个可调状态观测模型用于对永磁同步电机转子位置和速度估算,建立其自适应规律,并根据Popov渐进收敛性理论进行了设计稳定性。该方法以PMSM电机本身作为参考模型,电流模型作为可调模型,采用并联型结构辨识转速,可以在较宽的速度范围内观测转速和转子位置,对系统的抗扰动能力具有较强的鲁棒性,并采用空间矢量脉宽调制技术减小转矩脉动。仿真结果表明,模型参考自适应状态观测器能够在较高转速范围内追踪实际信号,实现对转子速度的观测,从而实现了无速度传感器磁场定向控制。
[1]王宏,于泳,徐殿国.永磁同步电动机位置伺服系统[J].中国电机工程学报,2004:151~155.
[2]王成元,郭庆鼎.矢量控制交流伺服驱动电动机[M].北京:机械工出版社,1994.
[3]郑萍,王明渝.感应电机无速度传感器矢量控制的速度估算器研究[J].电工技术学报,2001,16(5):24~29.
[4]Minghua Fu,Longya Xu.A Novel Sensor-less Control Technique for Permanent Magnet Synchronous Motor Using Digital Signal Processor(DSP).IEEE Aero space and Electronics Conference,1997,(1):403~408.
[5]贾洪平,孙丹,贺益康.基于滑模变结构的永磁同步电机直接转矩控制[J].中国电机工程学报,2006,26:134~138.
[6]Low TS,Lee TH,Chang KT.A Nonlinear Speed Observer for Permanent2 magnet Synchronous Motors.IEEE Trans Ind.1993,40(3):307 ~316.

