超图的奇圈横贯

朱俊杰

(昌吉学院数学系,新疆昌吉 831102)

超图的奇圈横贯

朱俊杰

(昌吉学院数学系,新疆昌吉 831102)

1997年,C.Berge提出了图 G奇圈横贯的定义,并用图G+K2研究了图G的奇圈横贯,最后得出结论, τ=n—-α(G+K2).将图 G的奇圈横贯推广到超图H上,并引入新概念 H+K2,得到超图 H的两个顶点x和z之间有奇长链的充分条件.

超图;奇圈横贯;H+K2

1 基本概念

定义1 令X=(x1,x2,…,xn)是一个有限集,关于 X上的一个超图,H=(E1,E2,…,Em),是 X上一个有限子集簇,使得,

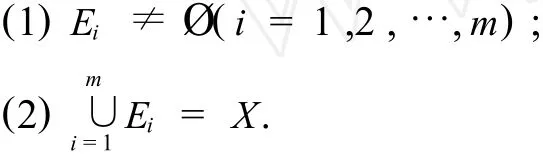
同时,一个超图,H=(E1,E2,…,Em),若还满足,

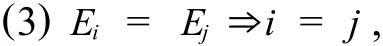
则称 H为简单超图.

对 j∈{1,2,…,m},r(H)=max|Ej|称为 H的秩,s(H)=min|Ej|称为 H的下秩.如果,r(H) =s(H),则称 H是一致超图.秩为 r的简单一致超图称为r-一致超图.

定义2 在超图H=(E1,E2,…,Em)中,一条长q链的链是指满足以下条件的序列(x1,E1,x2, E2,…,xq,Eq,xq+1).

(1)x1,x2,…,xq是H中不同的顶点;

(2)E1,E2,…,Eq是H中不同的边;

(3)对 k=1,2,…,q,xk,xk+1∈Ek.

若q＞1,且xq+1=x1,那么称这样的链为 H的q长圈.q为奇数称为奇圈,q为偶数称为偶圈.

定义3 对集合A⊂X,称HA=(Ej∩A|1≤j≤m,Ej∩A≠φ)为A对H的导出超图.对集合J⊂{1,2,…,m},称 H′=(Ej|j∈J)为J对H诱导的部分超图.H′的顶点集是X的一个非空子集.

2 超图的奇圈横贯

定义4 H是一个超图,复制H形成H′,a为H中任意一个顶点,a′是H′中对应a的顶点,用一条边连接a和a′,形成的超图我们称之为H+K2.连接a和a′的边叫顶点边.

定义5 超图的匹配是超图中两两不相交的边组成的集合,集合中的元素称为匹配边.用v(H)表示 H的最大匹配的边数.设 a是超图中的一个顶点,若 a包含在超图的一条匹配边e中,则称a是饱和的,也称e覆盖a.若超图中存在一个匹配满足其中的元素覆盖超图中的所有顶点则称这个匹配是超图,且是完美匹配.

定理1 H是连通简单超图,x和z是H中的两个顶点,若超图,H+K2-{x′,z′},存在有完美匹配,则 H中有一条x到z的奇长链.

证明 设H+K2-{x′,z′}中有完美匹配M,那么称这个完美匹配中的边为粗边,H中其他边称之为细边,下面做一条 x到z的奇长链.

因为H+K2-{x′-z′}中有完美匹配,存在一个顶点x1,使得x,x1在 H+K2-{x′,z′}的一条粗边中,记为 E1(E1∈H),且这是唯一包含 x的粗边(若d(x1)=1,则x1在H+K2-{x′,z′}也要饱和,那么包含 x′1的粗边只能是 E′1-x),顶点边 x1x′1必不在M中,否则与匹配矛盾.那么,存在一个顶点x2,使得x′1,x′2在H+K2-{x′,z′}的一条粗边中,记为(∈H′).同理,x2是顶点边的另一个端点,存在一个顶点 x3,使得 x2,x3在 H+K2-{x′,z′}的一条粗边中,记为 E3(E3∈H).如此,则形成一个奇长边序列,E1,E2,…,Ek,其中,x∈E1, z∈Ek,Ei∩Ei+1≠Ø,这里,Es(s为偶数)是 E′s在H中的对应边.

下证 Ei(I=1,2,…,k)是不同的边.

假设存在 Ei= Ej,(i＜j,i,j=0,1,2,…,k),设 xi1,xi2∈Ei,xi1,xi2∈{xi|i=1,2,…,k-1}, xi1∈Ei-1∩Ei,xi2∈Ei∩Ei+1和 xj1,xj2∈Ej,xj1, xj2∈{xj|j=1,2,…,k-1},xj1∈Ej-1∩Ej,xj2∈Ej∩Ej+1,由假设 xi1,xi2,xj1,xj2∈Ei= Ej.当 i,j奇偶性相同时,在 H+K2-{x′,z′}中,Ei,Ej要么同在 H中,要么同在 H′中,在奇长边序列 E1,E2,…,Ek中,用 xj2代替 xi2,去掉 Ei+1,…,Ej仍然可得x到z的一个奇长序列.当i,j奇偶性不同时,在H+ K2-{x′,z′}中,Ei,Ej一个在H中,一个在 H′中,不妨设 Ei∈H,Ej∈H′,由假设 xj2∈Ei,且 xj2∈Ej+1,因为在 H+K2-{x′,z′}中 Ei,Ej+1都是 H中的粗边,若 Ei≠Ej+1,则xj2被两条不同粗边包含,与匹配定义矛盾,因此 Ei=Ej+1.所以,在奇长边序列E1,E2,…,Ek中,用 xj2+1代替 xi2,去掉 Ei+1,…,Ej+1仍然可得 x到z的一个奇长序列.

由上述过程可看出,若 Ei,(i=1,2,…,k)中有相同的边,总可以去掉一些边使其变得更短且不改变其奇偶性,而 x和z之间的距离不可能无限短,因此存在奇长边序列 Ei,(i=1,2,…,k),它连接x和z,且是不同的边.

再证 x=x0,x1,x2,…,xk-1,xk=z是不同的点.

假设存在 xi= xj,(i≠j,i,j∈{0,1,2,…, k}),由 H+K2-{x′,z′}的性质知,在 H+K2-{x′,z′}中必存在H中的两条粗边包含xi和xj.由以上证明可知,这是两条不同的粗边,由于 xi=xj,(i≠j,i,j∈{0,1,2,…,k}),那么,xi被两条粗边包含,这与匹配的定义矛盾.因此,x=x0,x1,x2,…, xk-1,xk= z是不同的点.

此也证明了 H中存在一条x到z的奇长链.

定义6 设H=E1,E2,…,Em是一个超图,整数 k≥2.H的一个顶点k-着色是指对X的一个k-划分,使得 H的每条非环的边至少与两个类相交,即,

E∈H,|E|＞1⇒E■Si,(i=1,2,…,k)

Si中的顶点称为i色顶点.Si允许是空集,故只有环是单色边.使超图H有k着色的最小正整数k称为 H的色数,记为χ(H).

定义7 设超图H=(E1,E2,…,Em),则=,…,),其中⊆Ei,(i=1,2,…,m)称为H的子超图.若H任意的子简单超图都是两可

着色的,则称 H具有遗传两可着色性质.

定义8 设 H=(E1,E2,…,Em)是 H上的超图,若集合 T⊆X与H中每条边相交,即,

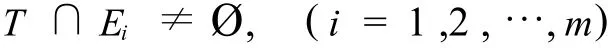
则称 T是H的横贯.

定义9 超图H的奇圈横贯是一个顶点集满足与超图中所有奇圈相交非空.基数最小的超图奇圈横贯称之为超图的最小奇圈横贯,它的基数记为τ′(H).不包含 H中任何奇圈的顶点集称为超图的奇圈独立集,基数最大的超图奇圈独立集称为超图的最大奇圈独立集,它的基数记为α′(H),显然有, τ′(H)=n-α′(H).H不包含任何基数大于1的边的顶点集称为 H的一个独立集,基数最大的独立集称为最大独立集,它的基数记为α(H).

定理2 若n个顶点的超图H具有遗传两可着色性质,那么,

τ′(H)=n-α(H+K2).

证明 设H的最小奇圈横贯为X-D,存在S, T满足,D=S∪T和S∩T≠Ø,由H具有遗传两可着色性质的定义,S∪T在H中的导出子超图是两可着色的.因此,S和T中都不包含H中的边.设在H+K2中,T′是T(∈H)在H′的像,那么S∪T′不包含H+K2中的H和H′,又因为S∩T=Ø,那么S∪T′不包含H+K2中的顶点边,所以S∪T′是 H+K2的一个顶点独立集.因为|S∪T′|=|S∪T|和|S∪T′|≤α(H+K2),故

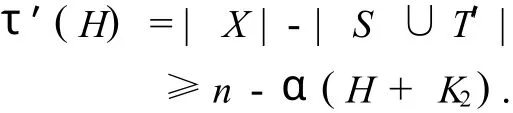
另外,设S∪T′为H+K2的一个最大顶点独立集,其中,S∈H,设 T是T′在H中的像,S和T中都不包含H中的边,所以S∪T在H中的导出子超图是两可着色的,那么S∪T在H中的导出子超图不包含奇圈,否则假设S∪T在H中的导出子超图包含奇圈,不妨设为 x1,E′1,x2,E′2,…,xk,E′k,x1,那么G={x1x2,x2x3,…,xkx1}是这个奇圈的子超图,所以G也是H的子超图,又因为H具有遗传两可着色性质,所以G={x1x2,x2x3,…,xkx1}是两可着色的,但 G是奇圈,所以一定不会两可着色,矛盾.

因此,S∪T也不包含H的奇圈,故,S∪T是H的一个奇圈独立集.

由于τ′(H)=n-α′(H),且|S∪T|≤α′(H),因此,

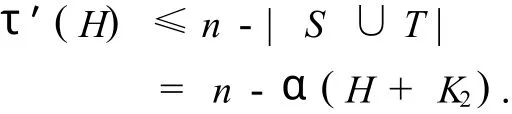
综上所述,

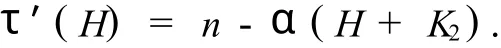
[1]Berge C.Hypergraphs：Combinatorics of Finite Sets[M].North Holland：Amsterdam,1973.

[2]Berge C,Fouquet J I.Odd the optimal transversals of the odd cycles[J].Discrete Mathematics,1997,169(2)：169-175.

[3]K ostochka A,Verstraete J.Even cycles in hypergraph[J].Journal of Combinatorial Theory(Series B),2005,94(1)：173-182.

[4]Dacar F.The cyclicity of a hypergraph[J].Discrete Mathematics,1998,182(1)：53-67.

[5]Gyárfás A,Jacobson M S,K zdy A E,et al.Odd cycles andθ-cycles in hypergraphs[J].Discrete Mathematics,2006,306(19-20)：2481-2491.

[6]BondyJ A.Theory with Applications[M].New Y ork：Macmillan Press,1976.

[7]Vishwanathans S.On2-coloring k-uniform hypergraphs[J]. Journal of Combinatorial Theory(Series A),2003,101(2)：168 -172.

[8]Acharya B D.Even Edge Colorings of a Graph[J].Journal of Combinatorial Theory(Series B),1983,35(1)：78-79.

[9]Alon N.Even Edge Colorings of a Graph[J].Journal of Combinatorial Theory(Series B),1985,38(2)：93-94.

[10]WangJianfang.Paths and cycles of hypergraphs[J].Science in China(Series A),1999,42(1)：1-12.

Odd Cycles Transversals of Hypergraphs

ZHU Junjie

(Department of Mathematics,Changji College,Changji 831102,China)

In 1997,C.Berge proposed the concept of the transversals of the odd cycles of Gin the second reference and made use of the graph G+K2to study the transversals of odd cycles of G,and gained the conclusion ofτ=n-α(G+K2).In this paper,the concept was promoted to hypergraph H and a new definition of the transversals of the odd cycles H+K2was formed.The sufficient conditions that an odd chain from the vertex x to the vertex z exists in H were obtained.

hypergraph;transversals of the odd cycles;H+K2

O157.5

：A

1004-5422(2010)02-0124-03

2010-01-25.

朱俊杰(1982—),男,硕士研究生,从事图论研究.