巧用“依托” 成就无痕教学

鄢晓钦

（福州市永泰县教师进修学校，福建 福州 350700）

教学的最高境界是无痕教学,其意义是不要让孩子们觉得你在教他们什么,而让孩子们在与老师、同学、文本互动的过程中去接受新知、启发心智。

但数学是理性的，孩子是感性的；数学是冰冷的，孩子是火热的；数学是单一的，孩子是丰富的。如何在数学与孩子之间寻找一条沟通的桥梁来成就无痕教学？这就需要为数学知识的呈现寻找适合的“依托”，以此吸引孩子，进而快乐地吸收、内化数学知识。

一、游戏依托，快乐求知

在小学阶段，很多新知识都组织孩子们在游戏中去获得，因为对于孩子来讲，经验就是结果，结果要靠直观形象的东西支撑，只有当经验积累到一定的程度，学生才会逐渐意识到这种现象中蕴涵着一定的数理，才会在这种新知的摸索中形成自己的思维。

例如，教学《比较数的大小》，将全班同学分成两个队，安排了如下三个抽签小游戏，以此来作为新知的依托，让孩子们快乐求知。

第一次抽签，从个位抽起

活动规则：①每次两队各派一个代表抽签；②第一次抽到的数字放在个位上，第二次抽到的放在十位上，第三次……③哪一队抽到的数字组成的四位数大，那一队就赢；④能确定胜负时，本轮比赛结束。

在这次游戏中让孩子们明白一个数理：两个数的位数相同，从高位比起，哪个数高位上的数大，那个数就大。

第二次抽签，从千位抽起

①每次两队各派一个代表抽签；②第一次抽到的数字放在千位上，第二次抽到的放在百位上，第三次……③哪一队抽到的数字组成的四位数大，那一队就赢；④能确定胜负时，本轮比赛结束。

第二轮活动的妙处就在于，“一战定乾坤”——由于首先就将抽到的数字放在最高位上，这就导致了初战即决战——最高位的数字大小直接决定了两个数的大小。在这个活动中让学生理解：两个数大小的比较，先看最高位。

第三次抽签

①每次两队各派一个代表抽签；②每一次抽到的数字由抽签者自己决定放在哪一位上；③哪一队抽到的数字组成的四位数大，那一队就赢；④能确定胜负时，本轮比赛结束。

第三轮游戏关键在帮助学生对位值制的深刻理解及对数感的直觉把握——“在相同数位上，不同的数大小不同；在不同的数位上，即使相同的数大小也不同。”

在这个游戏的过程中，孩子们会作如下思考：抽到的数字放在哪位呢？放在低位，如果后面抽到的数字更小怎么办？放在高位，后面如果抽到更大的数岂不是让自己立于失败之地？这里需要数感的直觉把握。

本案例的教学运用三个游戏为依托，唤醒孩子们对本知识相关的原知识——10以内数的大小比较和位值制的认识，让新、旧知识形成一个完整的知识链，新知的获取便水到渠成。

二、辩论依托，探询数理

数学的核心是思维，为了探寻数理，理清思路、辩论是一种行之有效的方法。如：学习了《三角形的面积》之后，为了提升对本节课知识的理解，课堂抛出学生经常困惑的一个问题：“等底等高的两个三角形面积相等，反之，面积相等的两个三角形一定就是等底等高的”。

面对新的问题，孩子们的直觉认为答案是肯定的，但部分孩子经过思考，会得出相反的结论，于是，老师在此时抓住契机，设计了一个问题辩论会。

生正方1：等底等高的两个三角形面积相等，那么面积相等的两个三角形当然就是等底等高的，这没什么好疑问的。就好比：你是你爸爸的儿子，你爸爸的儿子就是你吧！

生反方1：生活是生活，数学是数学，不能混为一谈。比如一个底为3厘米、高是2厘米的三角形与一个底为2厘米、高是3厘米的三角形底和高是不同，但它们的面积不是一样的吗？

生正方2：那也可能是巧合吧，总不能以一个特例来说明一个道理吧。

生反方2：这是我画的两个三角形（学生展示），通过测量得到，一个三角形的底是6厘米，高是2厘米，另一个三角形的底是3厘米、高是4厘米，请问他们的面积怎样？

生反方3：这是我列的一张表格，面积是20平方厘米，它们的底与高各不相同。

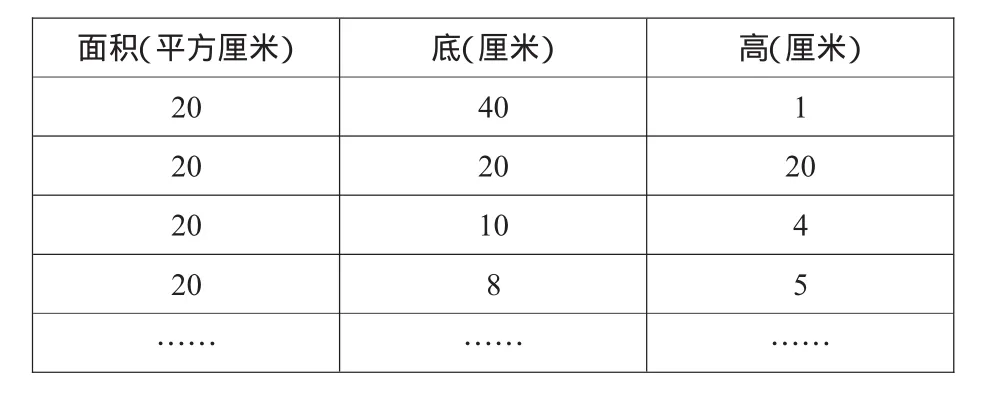
面积（平方厘米） 底（厘米） 高（厘米）20 40 1 20 20 20 20 10 4 20 8 5…… …… ……

生反方3：你们正方能举一个例子来说明你们的观点是正确的吗？

正方经过思考，确实还真举不出能说明自己观点的例子。

师：通过刚才的辩论，结论很明确了，正方同学，你们有什么想说的吗。

正方：同意他们的观点，看来，很多问题不能想当然的。

安排这么个辩论的环节，辩论双方的同学通过动脑思考、动手操作、动口表达，剖析数理。从字面文字、绘制图形、测量计算等方面收集素材并加以分析，说服对方。从而双方同学不仅增长了知识，锻炼了口才，还激起了自主探究的动机。一个本来说不清、道不明的问题，以辩论为依托，理清了、道明了，心服了。

三、整合依托，拓展内涵

学科本身并不是核心的内容，它们只是促进学生发展的媒体。为关注学生的发展，应打破学科之间的界限，促进学生整体发展。

例如，五年级上册《可能性》一课，其中要完成的一个教学目标是：体验事件发生的可能性与游戏规则的公平性之间的关系，学会用几分之一表示简单的可能性事件发生的可能性的大小。在学以致用的环节，我设计了一个玩飞行棋的游戏，将全班同学分为三组，红队、黄队、蓝队三方参与游戏，最后蓝队获胜。

游戏之后，设计一个问题。

师：如果刚才三方同学沿着这条棋路继续比下去，谁会是最后的赢家？

生1：不知道。

生2：可能是我们吧，嘻嘻……

生3：无法确定。

众生：对啊，对啊，谁都有可能获胜！

师：从中你们有什么感悟吗？

生5：谁笑到最后，谁就笑得最美，坚持！呵呵。

生6：比赛没有到最后，谁也不知道最后谁会获胜。

师：是啊，今天老师想告诉你们的是，棋如人生，人生如棋，生活亦是如此。我们要学会用不确定的眼光去观察、分析不确定事件的发生，不管结局如何，我们都要怀着良好的心态去下好这盘棋。

教师的天职是教书育人，我以“玩飞行棋”的数学活动为依托，向孩子们渗透一个思想：生活中有许多不确定事件的发生，我们无法确定最后的结局，但我们要怀着良好的心态，做好成长中的每一件事。

四、取材依托，点亮课堂

在一节公开课上，学习了《分类》一课的新知识，在课堂练习中，老师要求学生任选学具袋中的学具，以今天所学的知识为它们分分类。学具袋中有老师准备的纽扣、贴纸、图形等等。孩子们完成的很好，可这些实物都是没有生命的东西。于是，老师又抛出了一个问题：环顾四周，你们还可以将什么拿来分类？

生1：我为下面听课的老师分分类。

师：好啊，怎么分？

生2：以性别分，男老师、女老师。

生3：以戴不戴眼镜分，戴眼镜的老师和不戴眼镜的老师。

生4：以头发的长短分，剪短发的、长头发的。

生5：以性格的不同分，温柔的、豪气的。

生6：以爱好不同来分，爱唱歌、爱跳舞、爱书法、爱看电视等等。

生7：以口味不同来分，爱吃酸的、爱吃辣的、爱吃甜的等等。哈哈……

没有生命的东西只有外在形状与用途的不同，它的分类是单一的，对分类知识的理解和应用也有局限性。但将听课的老师拿来分类，那就融入了人的情感、爱好、需求等等，这样的分类更人文、也更生活化，对知识的理解也更透彻，从而也点亮一个原本单一的课堂。