我国货币政策自主性的实证研究

胡再勇

（外交学院 国际经济学院，北京 100037）

一、引言

对我国而言，增强汇率制度弹性以提高货币政策自主性是我国汇率政策改革考虑的一个重要因素（孙华妤，2006）。[1]但许多研究发现，货币政策自主性与汇率制度弹性之间并不存在系统性关系。如Hausmann等(1999)发现一些实行固定汇率制度的国家，其货币政策独立性还强于实行浮动汇率制度的国家；Bordo和Flandreau(2003)则认为，即使在传统的金本位制下，也存在显著的货币政策自主性；Calvo和Reinhart(2002)认为在浮动汇率制下，也只有有限的货币政策自主性；Forssback和Oxelheim(2006)认为在浮动汇率制与固定汇率制下，货币政策自主性并没有显著差异；而Frankel等(2004)发现，一些实行浮动汇率制或者固定汇率制的国家，它们的货币政策都不独立；孙华妤(2004)也认为，浮动汇率制度或者完全资本管制并不能保证货币政策的独立性。[2-7]因此，通过增强汇率制度弹性并不必然会提高货币政策自主性。2005年7月汇改以后，人民币汇率制度弹性大幅增强，那么我国的货币政策自主性有没有显著提高呢？这是本文研究的主要目的。一国的货币政策包括利率政策和货币数量政策，因此，本文拟从利率政策和货币数量政策两个角度去考察我国货币政策自主性在2005年汇改前后的变化情况，并据此实证检验“可能的二元”(Possible Duality)假设，即汇率制度弹性越高，货币政策自主性越强。

二、我国货币政策自主性的理论分析

本文首先对Mundell-Fleming模型(以下简称M-F模型)的代数形式进行修正，然后基于修正后的M-F模型，就1997年7月－2005年7月以及2005年7月汇改后两个时期，我国不同汇率制度弹性、资本流动性与货币政策自主性进行理论分析。①

M-F模型是粘性价格模型，资本完全不流动，国际收支平衡仅仅考虑经常账户的平衡。本文在M-F模型中纳入资本金融账户，并考虑我国国际收支不平衡的实际情况。修正后的M-F模型的代数形式如下：

其中，（1）式表示商品市场均衡时产出与利率的关系；（2）式表示货币市场均衡时货币供给量与利率的关系；而（3）式则为我国国际收支状况的等式。②在式中，y表示国民收入；e表示即期汇率；p*表示国外价格；p表示国内价格。由于M-F模型是粘性价格模型，两国价格差p*-p保持不变。α表示经常账户差额对真实汇率的敏感程度，假定满足马歇尔－勒纳(Marshall-Lerner)条件；β表示边际消费倾向；i表示利率；γ表示投资对利率的敏感度；g表示政府支出；m表示真实货币供应量，由国内信贷和国际储备决定；λ表示交易性和预防性货币需求对收入的敏感度；ω表示货币需求对利率的敏感度；δ表示边际进口倾向；π表示国际资本流动对利率的敏感度；Ef表示预期的远期汇率；ρ表示国际资本流动对预期汇率升（贬）值的敏感度；BP表示我国经常账户与资本金融账户的总盈余量。

在1997年7月至2005年7月的钉住汇率制度期间，人民币对美元波动幅度很小，因此ρ≈0。由于美元相对于其他全球主要货币自由浮动，因此，人民币对其他货币也是自由浮动的。但我国的国际储备以美元占绝对数量，再加上我国的资本账户还没有完全放开，也比较小，因此我国国际收支主要由经常账户决定。现在考虑钉住汇率制度下货币政策的自主性情况。假设外国利率i*提高（降低），这时资本外（内）流，但考虑到资本账户没有完全放开，资本外流有限，影响国际收支较小，对钉住汇率制的影响也较小。由于1997年7月到2005年7月之间，人民币兑美元汇率保持在8.27～8.28元人民币／美元之间，外国利率变动（提高或降低）导致的汇率变动可能高于也可能低于0.01元人民币／美元。如果导致汇率变动低于0.01元人民币／美元，则可以不采取应对措施。但在外国利率变动既定的情况下，本国利率或货币数量变动带来的汇率变动趋势，不可能超过0.01元人民币／美元的幅度，因此本国存在一定的货币政策自主性。若外国利率提高（降低）导致汇率变动高于0.01元人民币／美元，则必须采取对应措施，使汇率波动小于0.01元人民币／美元。这时可以采取紧缩性（扩张）货币政策或财政政策，减小汇率波动的幅度，但这会使本国的利率提高（降低），因此本国利率随外国利率的变动而变动，本国的货币政策没有自主性。

2005年7月汇改后，我国的汇率制度是参考一篮子货币进行调节、有管理的浮动汇率制度，人民币汇率波动幅度较大，因此ρ≠0。但我国的资本账户没有完全开放，π较小。M-F模型假设抛补的利率平价成立，即i-i*=(f-e)/e，本文进一步假设市场上的大部分投资者对汇率的预期准确，即预期的远期汇率恰好等于到期的远期汇率，这时抛补和非抛补的利率平价都成立，即i-i*=(Ef-e)/e=(f-e)/e，(3)式可以写为α(e+p*-p)-δy+(π+ρ)(i-i*)=BP。在有管理的浮动汇率制下，由于存在较强的人民币升值预期，|ρ|不小，假设外国利率i*降低，这时资本内流，再加上存在强烈的人民币升值预期，即系数|π+ρ|较大，资本通过各种渠道进入的数量不少。这一方面会导致人民币升值更多；另一方面，被动的货币供给增加，使得本国的货币数量政策缺乏自主性。货币供给增加将导致本国利率i降低。为了避免本国利率i降低，我国政府采取的措施是，通过被动增加货币供给的方式以吸收外国资本，同时发行央行票据以收紧市场上的流动性，避免货币供应量的增加和利率的下降。但这带来了央行发行成本的增加。只要资本内流的规模在央行的吸收能力之内，我国利率并不会随着外国利率的下降而同等幅度的下降，我国存在较大的利率政策自主性。若资本内流的规模超过了央行的控制能力，如被动发行央行票据超出了央行成本承担的范围，则央行不可能采取完全的冲销措施，于是短期内我国利率随外国利率的降低而降低，缺乏自主性。若外国提高利率i*，则存在资本外流，但人民币升值预期导致资本内流，且资本项目管制导致的资本外流没有人民币升值预期导致的资本内流大，外国提高利率和人民币升值预期的综合效果仍然是资本内流。这时我国政府可以采取同样的措施，其力度也较利率i*下降时小，结果仍然是我国货币数量政策没有自主性，而利率政策存在较大的自主性。

综上所述，在1997年7月至2005年7月间，如果外国利率或货币数量变动导致人民币汇率波动小于0.01元人民币／美元，则我国存在货币政策自主性；若外国利率或货币数量变动导致人民币汇率波动大于0.01元人民币／美元，则我国丧失了货币政策自主性。在2005年汇改后，我国的货币数量政策是被动的、缺乏自主性的，但只要央行的冲销政策不超出央行的成本承担范围，我国还是存在一定的利率政策自主性。

三、本文的实证方法和模型

对于货币政策自主性的实证研究，主要有三种研究方法。③为了准确度量我国利率政策自主性的变化情况，本文准备同时利用货币目标区模型和货币政策反应方程来实证研究我国利率政策在2005年汇改前后的变化情况；同时，利用长短期外汇储备与基础货币之间的关系来实证研究我国货币数量政策在2005年汇改前后的变化情况。

（一）基于货币目标区模型考察利率政策自主性的实证方法及模型

货币目标区模型的中心假设是非抛补的利率平价条件(UIP)：

式中，it和分别表示本国和外国的利率。考虑到美国、欧元区以及日本的经济影响力，本文初步使用美元利率、欧元区利率以及日本利率代表外国利率；但实证中发现，日元利率和其他利率之间存在严重的多重共线性，因此，外国利率最终以美元利率和欧元区利率为代表。Δe表示汇率变化，E是预期算子，Ωt表示在t时刻对t到t+k时段汇率变动进行预期所拥有的信息。目标区模型的中心论点是目标区允许国内利率相对于外国利率暂时偏离，而偏离的大小和时间长度则度量了货币政策自主性的程度。这种论点也适用于其他汇率制度。例如，缺乏可信度的货币政策当局，即使在弹性汇率制度下，也没有多少货币政策自主性；相反，专注于通货膨胀和产出的具有可信度的货币政策当局，即使在弹性汇率制度下，其利率可以持续地偏离外国利率(Fratzscher，2002)。[8]本文利用外国利率溢出效应的大小和本国利率向长期均衡关系调整的速度来度量货币政策自主性的程度。

考虑到利率数据的特点，即利率数据是非平稳的，其一阶差分都是平稳的，而且是有偏的尖峰分布，因此，应考虑利用广义自回归条件异方差模型(GARCH)来实证分析利率平价关系。考虑到汇率一阶差分也是平稳的，不妨假设预期是无偏的，这样就可以去掉预期符号。实证模型采取的形式为式（5）和式（6）：

其中，β系数表示利率的传导；κ可以解释为由于国内外利率不一致产生的风险溢价。

式(6)表示条件方差是其自身的滞后项和自身的平方项的函数。GARCH模型通过采用极大似然函数法进行估计，极大似然函数的对数形式为：

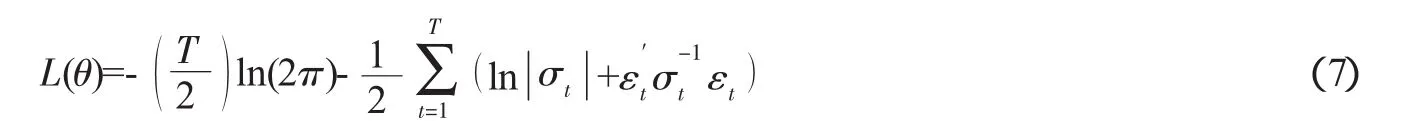
其中，T是样本观测值个数、θ是相关的参数列向量、σt是随时间变化的条件方差－协方差矩阵。通过单纯形算法（Simplex Algorithm），可以得到参数的初始值；再通过Berndt等(1974)提出的极大化数值算法，[9]可以得到最终的参数估计值。

利用GARCH模型来模拟本国利率和外国利率之间的长期关系，必须考虑利率水平数据的平稳性问题。如果GARCH模型（5）式中的εt是平稳的话，则（5）式衡量了本国利率和外国利率之间的长期协整关系。但即使长期协整关系成立的话，GARCH模型也无法度量系统的短期动态调整过程。而为了度量货币政策的自主性程度，需要了解利率偏离长期均衡是如何持续的以及利率调整到均衡水平的速度如何。偏离的时间越长，或者调整的速度越慢，则货币政策自主性越强。使用误差修正模型（Error Correction Model,ECM）可以度量短期动态调整过程，而误差修正模型其实是（5）式的变形。如下式所示：

其中，参数λ度量了利率向长期均衡水平调整的速度；ecm是式（5）中的平稳残差项；Δ前的系数度量了外国利率变化的短期溢出效应大小。

可以利用Engle和Granger(1987)提出的E-G两步法来确定和估计误差修正模型。[9]第一步是估计(5)式，并判断残差项是否平稳；若平稳，则(5)式就是本国和外国利率的长期协整关系。第二步利用第一步得到的平稳残差项表示ecm，并估计(8)式，得到其他的参数。

（二）基于货币政策反应方程考察利率政策自主性的实证方法和模型

本文修改Clarida等(1998)构建的货币政策反应方程，[10]加入外国货币政策变量，以检验我国的货币政策变量到底是由国内的宏观经济变量(如最优通货膨胀率预期偏差、产出差)所驱动，还是受国外的货币政策决策所影响。央行主要的货币政策工具是短期利率，本文利用银行间隔夜贷款利率作为货币政策工具。为了使本文构建的货币政策反应方程有意义，假设存在暂时的名义工资和价格刚性。在刚性条件下，央行货币政策在短期能影响实际活动；通过改变名义利率，央行能改变实际利率和汇率。在不完全的工资和货币调整下，产出和通货膨胀率间存在短期的正向关系，这会对央行的货币政策产生约束作用(Clarida，1998)。[10]央行在两次利率变动期间有短期的名义利率目标re，而短期的名义利率目标依赖于经济状况，本文假设短期利率目标依赖于预期的通货膨胀率和产出，方程如下：

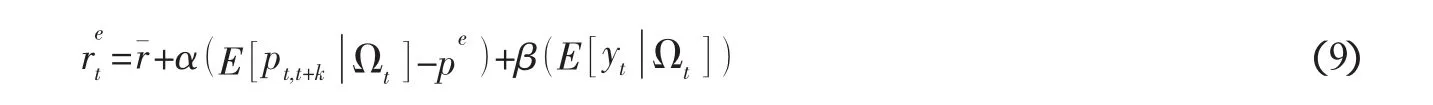
其中，是长期均衡名义利率；pt,t+k是t和t+k期间的通货膨胀率；pe是通货膨胀率目标；yt是实际产出水平与潜在产出水平的差；E是预期算子；Ωt表示央行在时刻t设定利率时所拥有的信息。

假设实际利率的调整部分取决于利率目标，则：

此处加入外国利率，是为了衡量外国货币政策对本国的影响；参数ρ2显著，即表明本国利率受到外国货币政策的显著影响，从而自主性受到了影响；参数ρ1是为了衡量本国利率的平滑度，0≤ρ1≤1。上述模型还包括对利率的随机冲击变量μt，假设μt服从独立同分布白噪声过程。

将式 （9） 代入式 （10） 中，并令 λ=-αpe，得到：

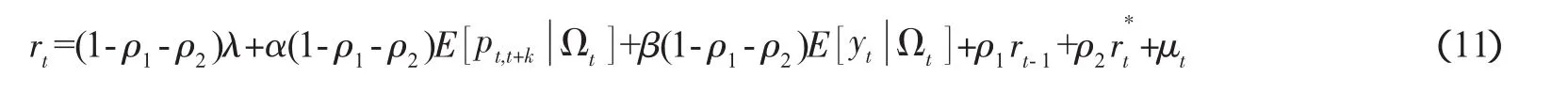
消除模型（11）中不可观测的预期变量，用实际变量进行替换，得到新的可用于计量实证的模型为：

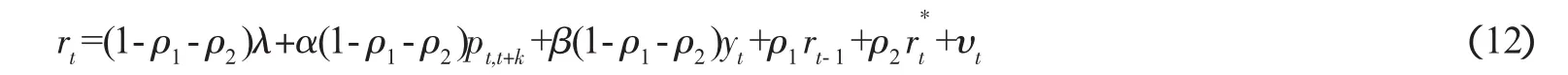
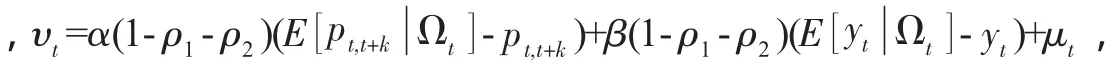
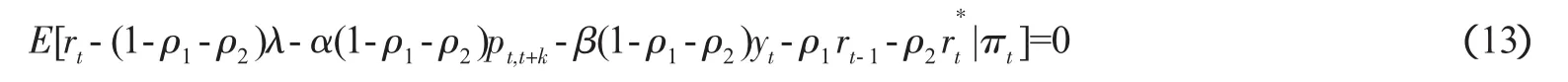
利用GMM法估计模型(13)，即可得到参数α、β、λ、ρ1和ρ2。工具变量集合πt可取通货膨胀率、产出、本国利率、外国利率、价格等的滞后项作为工具变量。

（三）基于外汇储备和基础货币长短期关系考察货币数量政策自主性的实证方法和模型

考虑到外汇储备变化可能对一国的货币供应产生影响，因此，一国的货币供应可以分为能由外汇储备预测的部分和不能由外汇储备预测的部分。其中，能由外汇储备预测的部分代表外部的影响；不能由外汇储备预测的部分则反映国内相应部门对货币供应的冲击，代表本国货币数量政策的自主性。Veyrune(2007)正是基于上述原理，利用外汇储备和基础货币之间的长期和短期关系来考察货币政策的自主性。[11]假设外汇储备和基础货币供应之间存在长期关系，如下式：

其中，Mt表示基础货币；Rt表示外汇储备；α表示基础货币对外汇储备的回归系数，即外汇储备的变化带来的基础货币的变化量；αRt表示基础货币供应可由外汇储备预测的部分；随机项μt表示基础货币供应中不能由外汇储备预测的部分，即表示本国相应部门对货币供应的冲击，用来刻画本国货币数量政策的自主性。若（14）式表示的基础货币与外汇储备的关系是长期的，则如果μt是非平稳的，表明本国货币政策存在一定的自主性；如果μt是平稳的，则表明本国货币政策不存在自主性。在非完全钉住汇率制度下，基础货币对外汇储备的弹性大于0小于1，本国相应部门对货币供应的影响不再是随机的，这时随机项非平稳，货币政策存在一定的自主性。自主性程度的大小随基础货币对外汇储备弹性的增大而降低。

若（14）式协整关系成立，则可以建立误差修正模型，以反映基础货币与外汇储备之间的短期变动关系。误差修正模型可以反映系统由短期偏离向长期均衡关系调整的速度。

四、实证结果及分析

（一）基于货币目标区模型考察利率政策自主性的实证结果

基于货币目标区模型衡量利率政策自主性用到的数据有：中国居民三个月的存款利率i、伦敦市场欧洲美元三个月的存款利率、欧元区的基准利率、人民币兑美元的即期汇率s。所有数据的频率均为日频率数据，其中，中国居民三个月的存款利率及伦敦市场欧洲美元三个月的存款利率数据，来源于CEIC数据库；人民币兑美元的即期汇率数据，来源于国家外汇管理局官方网站；欧元区基准利率数据，来源于欧洲央行官方网站。由于要考察2005年7月21日汇改前后我国货币政策自主性情况，为了使汇改前后两个区间的样本数据长度差不多，本文使用的数据范围为2001年1月2日到2009年7月23日。④考虑到需要计算三个月后汇率相对于即期汇率的变化值Δe，因此实际样本范围从2001年1月2日至2009年4月24日。考虑到中国、欧洲的节假日不一样，且利率数据在节假日延续，而即期汇率只有在工作日才有报价，因此本文对数据进行了调整，只保留在同一天都有数据的样本，最后得到的样本数为2056个。汇改前的样本区间是2001年1月2日至2005年7月21日，样本个数为1140个；汇改后的样本区间是2005年7月22日至2009年4月24日，样本个数为916个。

1.汇改前后两个区间的GARCH模型实证研究

（1） 汇改前均值方程为：

均值方程的残差记为resid01。方差方程为：

(2)汇改后均值方程为：

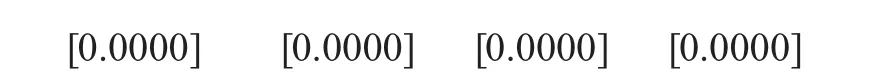
均值方程的残差记为resid02。方差方程为：

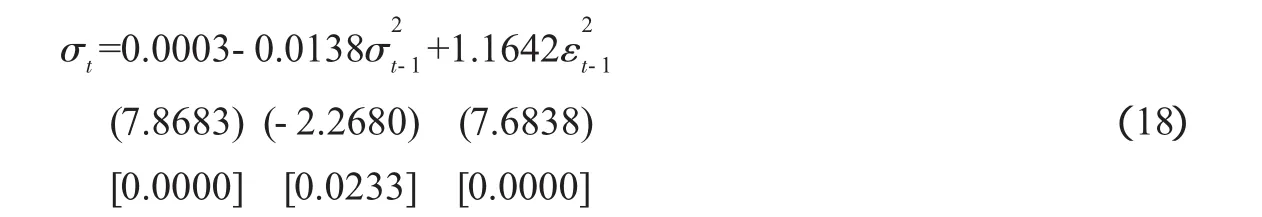
在上述方程中，圆括号中的数字是相应回归参数的z统计量，而方括号中的数字是相应z统计量的p值。从p值可见，所有回归参数都在5%的水平上显著。

2.残差序列的ADF平稳性检验

ADF平稳性检验结果见表1。

表1 ADF平稳性检验

从ADF平稳性检验结果可知，残差序列Resid01和 Resid02在5%的水平上都平稳，因此，方程（15）和（17）分别表示了汇改前、汇改后两个区间我国利率和外国利率之间的长期协整关系。从协整方程（15）和（17）可见，汇改前美元利率对我国利率的水平溢出效应是正的，美元利率的长期回归系数为0.0139；而汇改后的溢出效应是负的，且汇改后整个区间内美元利率的长期回归系数为-0.2435。此外，欧元区利率对我国利率的溢出效应都为正，但汇改前欧元区利率对我国利率的溢出效应较汇改后的溢出效应要小很多；汇改前欧元区利率的长期回归系数为0.0856，而汇改后欧元区利率的长期回归系数为0.5476。

3.汇改前后两个区间的误差修正模型实证研究

由于方程（15）、（17）都是协整方程，因此，可以进一步建立误差修正模型，以考察短期动态变化关系。

（1）汇改前误差修正模型为：

其中，ECM是长期均衡偏差项，等于长期协整方程（15）的残差项Resid01。

（2）汇改后误差修正模型为：

其中，ECM是长期均衡偏差项，等于长期协整方程（17）的残差项Resid02。

在误差修正模型（19）和（20）中，圆括号中的数字是相应回归参数的t统计量，而方括号中的数字是相应t统计量的p值。从p值来看，除方程（20）的ECM回归参数在10%水平上显著外，其他回归参数都在5%水平上显著，表明回归结果较好。从实证结果来看，两个误差修正模型ECM项前的系数都为负，表示长期均衡偏差项对被解释变量偏离长期均衡项起着负向的修正作用，符合误差修正模型反向修正的基本原理。

下面分析两个区间段利率调整到均衡水平的速度如何？汇改前，美元利率的长期回归参数为0.0139，而该区间内向长期均衡调整的速度为-0.0092，意味着半衰期为1.51天；汇改后，美元利率的长期回归参数为-0.2435，而该区间内向长期均衡调整的速度为-0.0073，意味着该区间内半衰期为33.36天。从半衰期可见，利率调整到均衡水平的速度在汇改后较汇改前要慢，意味着汇改后我国利率偏离长期均衡水平的持续期较汇改前要长。因此，汇改后我国货币利率政策自主性较汇改前要强。

（二）基于货币政策反应方程考察利率政策自主性的实证结果

基于货币政策反应方程衡量资本流动性用到的数据有：上海银行间隔夜拆借利率的月平均值i（%）、美元隔夜拆借利率的月平均值i*（%）、月度居民消费价格指数p（%）、月度工业增加值g（亿元）。此外，为了GMM估计中工具变量的需要，本文还用到的数据有：月度进出口总值tr（亿美元）、月度工业总产值gp（亿元）、月度社会消费品零售总额cz（亿元）、月度工业品出厂价格指数pg（%）。数据范围从2002年1月至2009年6月，其中上海银行间隔夜拆借利率和美元隔夜拆借利率数据来源于CEIC数据库。原始数据为日频率数据，本文将每月的日频率数据加总后除以月度的数据个数，得到月平均隔夜拆借利率数据。其他数据来源于和讯网。

在进行实证前，本文用月度工业增加值表示实际产出水平，用月度工业增加值滤波后得到的趋势值表示潜在产出水平；实际产出水平与潜在产出水平的差就是产出差。对月度工业增加值g进行HP(Hodrick-Prescott)滤波，得到月度工业增加值的趋势值g1,则实际产出水平与潜在产出水平的差y=g-g1。

1.汇改前我国货币利率政策自主性变化情况

利用GMM方法估计（13）式，得到回归结果为：

拟合优度为0.7251，表明回归方程拟合效果较好。布罗施－戈弗雷序列相关的拉格朗日乘数检验（Breusch-Godfrey Serial Correlation LM Test）结果为：LM(1)=2.5947，其对应的p值为0.1072；LM(2)=4.0839，其对应的p值为0.1298；LM(3)=4.2199，其对应的p值为0.2387。这表明回归方程（21）式的残差不存在自相关。

从（21）式可知，ρ1=0.6072、ρ2=-0.1824、1-ρ1-ρ2=0.5752，满足利率部分调整模型的相关系数设定，即0≤ρ1≤1、0≤1-ρ1-ρ2≤1。此外，根据回归结果也可以计算得到λ、α和β的值，即λ=1.9079、α=-0.0122、β=-1.32E-04。

从回归参数的显著性来看，价格指数pt和产出差yt的回归参数不显著，常数项在5%的水平下显著；而上一期的利率it-1和美元隔夜拆借利率月度均值的回归参数，在1%的水平下都显著。这表明在2002年1月至2005年6月，我国利率政策的反经济周期性作用并不明显，而主要受美元利率的影响；此外，利率的部分调整模型意味着我国利率还受到上一期利率影响。

2.汇改后我国货币利率政策自主性变化情况

在实证过程中，发现利用OLS得到的回归方程只存在三阶自相关，而不存在异方差，因此考虑利用科克伦－奥卡特（Cochrane-Orcutt）迭代法进行估计。估计结果为：

拟合优度为0.7566，表明回归方程拟合效果较好;此外，F统计量表明回归方程整体显著。怀特异方差检验结果为：不含交叉项时，怀特统计量WT=11.4564，其对应的p值为0.1772；含交叉项时，怀特统计量WT=14.2971，其对应的p值为0.4278。这表明不存在异方差。布罗施－戈弗雷序列相关的拉格朗日乘数检验结果为：LM(1)=0.1595，其对应的p值为0.6896；LM(2)=2.4081，其对应的p值为0.3000；LM(3)=3.1971，其对应的p值为0.3622。这表明残差不存在序列相关性。

从（22） 式可知，ρ1=0.6587、ρ2=0.0402、1-ρ1-ρ2=0.3011，满足利率部分调整模型的相关系数设定，即0≤ρ1≤1、0≤1-ρ1-ρ2≤1。此外，根据回归结果也可以计算得到 λ、α 和 β 的值，即 λ=1.1252、α=0.1538、β=6.64E-04。α和β的符号符合利率作为反经济周期工具的经济含义，即物价越高，利率越高；产出差越大，利率越高。

从回归参数的显著性来看，所有回归参数在5%的水平下显著。其中价格指数pt的回归参数为0.0463，表明我国的利率政策有明显的反通货膨胀作用，这和我国严格控制通货膨胀的宏观经济政策是一致的。再来看利率调节产出差的作用。产出差yt的回归参数为0.0002，这和利率作为调节宏观经济的目标相一致，表明我国利率也是调节产出差的政策工具。同时也表明汇改后，我国利率政策的反经济周期性作用比较明显。此外，美元隔夜拆借利率月度均值前的回归参数为0.0402，在5%的水平下显著，表明我国利率还受到美元利率的影响。从回归结果（22）式可知，我国利率主要受到宏观经济目标如通货膨胀率、产出差以及美元利率的影响；此外，利率的部分调整模型意味着我国利率还受到上一期利率的影响。

比较（21）和（22） 式中美元隔夜拆借利率月度均值前的系数，即汇改前前的系数为－0.1824，汇改后前的系数为0.0402，很显然，汇改前美元利率对我国利率的影响更大，这表明汇改后较汇改前我国利率政策的自主性更大。

（三）基于外汇储备和基础货币长短期关系考察货币数量政策自主性的实证结果

实证使用的数据是基础货币以及外汇储备。数据来源于CEIC数据库，数据频率为月度，数据长度从1997年1月到2009年6月。基础货币（BS）的单位为10亿元人民币，外汇储备（R）的单位为10亿美元。

两个回归方程分别为（23）和（24），回归残差分别用resid03和resid04表示。

1.汇改前回归方程为：

2.汇改后回归方程为：

回归方程下面圆括号内的数据是t统计量，而中括号内数据是相应的P值。从回归方程（23）和（24）可见，回归参数都显著，表明基础货币供应可由外汇储备部分预测到；如果残差项是非平稳的，则我国货币政策存在一定的自主性。两个回归方程残差resid03和resid04的平稳性检验结果见表2。

表2 残差的ADF平稳性检验

当残差项非平稳时，表明本国货币数量政策存在一定的自主性。因此，方程（23）的残差非平稳表明，汇改前我国货币数量政策存在一定的自主性。方程（24）的残差在5%的水平下平稳，表明我国货币数量政策没有自主性，基础货币以央行购买外汇储备的形式被动地供应。这主要是因为汇改后，人民币兑美元汇率由2005年7月21日的8.2765元人民币／美元，升值到8.11元人民币／美元，一步升值2.053%；随后，由于贸易顺差不断扩大，外汇储备急剧增加，人民币不断小幅升值，而外界预期人民币会进一步升值，热钱通过各种渠道流入中国，导致基础货币投放被动地不断增加，货币数量政策缺乏自主性。

五、结论及启示

本文首先针对我国的实际情况，对Mundell-Fleming模型的代数形式进行了修正，即在粘性价格、资本完全不流动、国际收支平衡仅仅考虑经常账户平衡的M-F模型的基础上纳入资本账户，并用以分析2005年7月汇改前后我国货币政策自主性情况。其次，本文利用货币目标区模型、货币政策反应方程以及外汇储备与基础货币之间的关系方程，实证研究了2005年7月汇改前后我国货币政策自主性的变化情况。据此，本文得到以下结论和启示。

1.基于货币目标区模型以及货币政策反应方程的实证研究结果都表明，汇改后我国的利率政策自主性较汇改前要强。

2.基于外汇储备和基础货币之间长期关系的实证结果表明，1997年1月至汇改前，我国货币数量政策存在自主性；汇改后，我国货币数量政策则缺乏自主性。

本文研究结论表明了“可能的二元”假设，即汇率制度弹性越高、货币政策自主性越强这一假设在我国也只是部分成立，亦即只对利率政策成立，而对货币数量政策并不成立。

本文的结论对我国货币政策也有启示作用。由于汇改后我国利率政策较汇改前的自主性程度提高，而货币数量政策则由汇改前的存在自主性变为缺乏自主性，因此，我国应以利率作为货币政策中介目标。

注 释：

①本处之所以将汇改前的区间选择从1997年7月至2005年汇改前，是因为1994年1月1日我国实行以市场供求为基础的、单一的、有管理的浮动汇率制后，除1994年1月1日至1997年7月1日，人民币兑美元汇率波动幅度较大外，从1997年7月至2005年7月，人民币兑美元汇率都保持在8.27～8.28元人民币／美元之间，汇率制度由开始的有管理的浮动汇率制变成事实上的钉住美元的钉住汇率制。这样，汇改前的区间实际为盯住汇率制；而2005年汇改后，我国实行以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度。汇改前后两个区间实行的汇率制度差别明显，便于本文的理论分析和实证研究。

②由于我国国际收支账户并不平衡，除1998年外，从1997年到2008年，我国存在经常账户和资本金融账户双顺差；即使在1998年，我国经常账户（2932351万美元）和资本金融账户（-632144万美元）余额之和仍为顺差。变量BP为衡量我国经常账户与资本金融账户总盈余量，因此为一正数。加入BP是为了使（3）式为恒等式。

③具体参阅Bertola和Svensson（1993）、Svensson（1994）、Clarida等 （1998）、Ball（1999，2000） 以及Veyrune（2007） 等文章。

④因为没有2001年1月1日的即期汇率数据，所以从2001年1月2日开始。

：

[1]孙华妤.中国货币政策独立性和有效性检验——基于1994－2004年的数据[J].当代财经，2006，(7)：26-32.

[2]Hausmann,Ricardo,Michael Gavin,Carmen Pages and Ernesto Stein:Financial Turmoil and the Choice of Exchange Rate Regime[R].Inter-American Development Bnak,Research Department Working Paper No.400，1999.

[3]Michael D.Bordo&Marc Flandreau:Core,Periphery,Exhcnage Rate Regiems,and Globalization[G].National Bureau of Economic Research,Inc.NBER Chapters in Globalization in Historical Perspective,2003,417-472.

[4]Calvo,Guillermo,and Carmen Reinhart:Fear of Floating[J].Quarterly Journal of Economics,2002,117(2):379-408.

[5]Forssback,J.,and L.Oxelheim:On the Link Between Exchange Rate Regimes,Capital Controls and Monetary Policy Autonomy in Small Eurpoean Countries,1979-2000[J].World Economy,2006,29:341-680.

[6]Frankel,J.A.,S.L.Schmukler,and L.Servén:Global Transmission of Interest Rates:Monetary Independence and currency Regime[J].Journal of International Money and Finance,2004,23:1-33.

[7]孙华妤.“不可能三角”不能作为中国汇率制度选择的依据[J].国际金融研究，2004，(8)：11-16.

[8]Marcel Fratzscher:The Euro Bloc,the Dollar Bloc and the Yean Bloc:How Much Monetary Policy Independence can Exchange Rate Flexibility Buy in an Interdependent World[R].European Central Bank Working Paper,2002,154：1-43.

[9]Berndt,E.K.,B.H.Hall,R.E.Hall and J.A.Hausman:Estimation and inference in nonlinear structural models[J].Annals of Economic and Social Measurement,1974，(3)：653-665.

[10]Clarida Richard,Jordi Gali,and Mark Gertler:Monetary Policy Rules in Practice:Some International Evidence[J].European Economic Review,1998,42(6)：1033-1067.

[11]Romain Veyrune:Fixed Exchange Rates and the Autonomy of Monetary Policy:The Franc Zone Case[R].IMF Working Paper,2007,34：1-23.

[12]Engle,R.and Granger,C.Cointegration and error correction:representation,estimation and testing[J].Econometrica,1987,55：251-276.