半p−预不变拟凸函数及其性质

王兴国

(温州大学瓯江学院，浙江温州 325035)

半p−预不变拟凸函数及其性质

王兴国

(温州大学瓯江学院，浙江温州 325035)

定义了两类广义不变拟凸函数——p−预不变拟凸函数和半p−预不变拟凸函数，探讨了半p−预不变拟凸函数的性质．所得结果比有关文献的结论更具一般性．

半p−不变凸集；半(p, r)−预不变凸函数；半p−预不变拟凸函数

函数的凸性在数学规划中有着重要的作用，有许多研究致力于引入各种广义凸函数、广义拟凸函数、广义伪凸函数来推广函数的凸性，以扩大其应用范围．文献[1]提出了预不变凸函数．文献[2]提出了预不变拟凸函数，并给出了它的某些性质及运用．最近，文献[3]在定义了p−不变凸集的基础上提出了(p, r)−预不变凸函数，它是预不变凸函数的推广．文献[4]提出了半连通集，并在此基础上提出了半预不变凸函数的概念．进一步地，文献[5]又定义了一类广义凸集——半p−不变凸集（它是半连通集、p−不变凸集的推广），并结合半预不变凸函数和(p, r)−预不变凸函数，定义了一类广义凸函数——半(p, r)−预不变凸函数，同时讨论了它的性质和它在极值问题中的应用．

受文献[3-5]的启发，笔者对文献[2]的预不变拟凸函数进一步研究，给出其推广——p−预不变拟凸函数、半p−预不变拟凸函数．鉴于半p−预不变拟凸函数是p−预不变拟凸函数的推广，本文仅探讨半p−预不变拟凸函数的性质及其在数学规划问题中的应用，所得结果较文献[2]、[6]的相关结论更具有一般性．

1 预备知识

则称S是关于η的半p−不变凸集．

定义 2[5]设S⊂的半p−不变凸集，若函数f:S→R在 u∈S处对任意x∈S，都有：

则称f是S上u处关于ϕ的预不变拟凸函数．若对任意x, u∈S，以上关系式成立，则称f是S上关于ϕ的预不变拟凸函数．

2 p−预不变拟凸函数和半p−预不变拟凸函数

二是，以关心对方的方式来表示自己的内疚之心。例如，在路上不小心踩到了一位陌生人的脚，我们通常会马上对受害者说“对不起，你没事吧？”这就是在道歉的同时，关心受伤害者的情况，从而减轻自己的错误程度，从心理上寻求一点的慰藉。

考虑上述定义，本文给出如下的一类广义拟凸函数的定义：

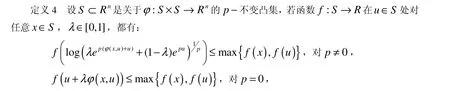
注4：容易看出任何一个半(p, r)−预不变凸函数都是半p−预不变拟凸函数．

证明：因为f:S→R是S上关于η的半p−预不变拟凸函数，对p≠0，有：

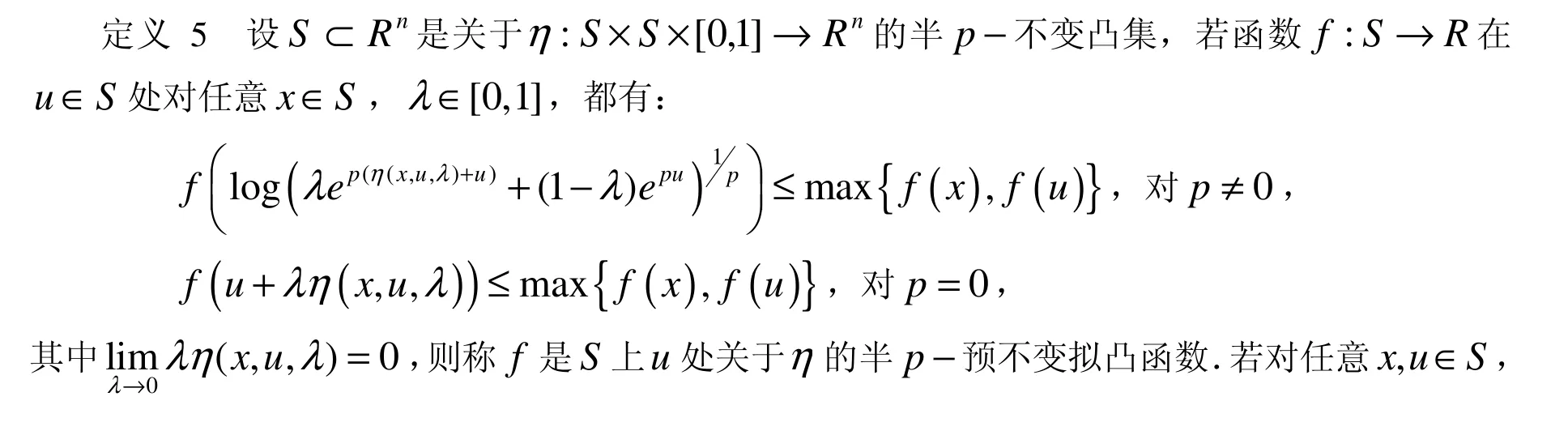
易证，在此证略．

则称f是S上u处关于ϕ的p−预不变拟凸函数．若对任意x, u∈S，以上关系式成立，则称f是S上关于ϕ的p−预不变拟凸函数．以上关系式成立，则称f是S上关于η的半p−预不变拟凸函数．

一个年纪已经过了六十的老人扛了一对大傀儡从后海走来，到了场坪，四下望人，似乎很明白这不是玩傀儡的地方，但莫可奈何的停顿下来。

3 半p−预不变拟凸函数的性质

定理 2 若f是半p−预不变拟凸函数，则对任意α∈R，α>0，αf是半p−预不变拟凸函数．

定理1 若f是半p−预不变拟凸函数，则对任意α∈R，f+α是半p−预不变拟凸函数．

重症患者低磷血症发病率高，低血磷组的医院生存率较正常血磷水平组低，是重症患者 预后指标之一，及时发现并纠正低磷血症应该受到广大医师的重视。

注3：当p=0时，p−预不变拟凸函数就是文献[2]中的预不变拟凸函数；当p=0时，半p−预不变拟凸函数我们可称其为半预不变拟凸函数．

定理3 设S⊂nR，若f:S→R是S上关于η的半p−预不变拟凸函数，g: R→R是一个非减函数，那么复合函数gg: R→R是S上关于η的半p−预不变拟凸函数．

锐骐6虽然是一款皮卡车型，但是在外观设计上也费尽心思。“冠军腰带式”前格栅，粗壮有力，安全感十足。横向镀铬连接LED日间行车灯，整体营造出时尚硬朗的前脸造型。饱满有力的全侧腰线，配合16寸银色涂装铝合金轮毂，使得锐骐6更具力量感。

1）f的严格局部极小点都是严格全局极小点；

2）f的全局极小点集是关于η的半p−不变凸集．

因此，M是关于η的半p−不变凸集．

⑧柳永《卜算子》(江枫渐老)：双调89字，上阕8句45字4仄韵，下阕8句44字5仄韵。句式：4464635346。5544635345。

注5：定理6表明，半p−预不变拟凸函数在数学规划的极值问题上具有重要的意义．

[1] Ben-Israel A, Mond B. What is invexity? [J]. Journal of Australian Marhemarical Society: Series B, 28: 1-9.

[2] Yang X M, Yang X Q, Teo K L. Characterazition and applications of prequasi-invex functions [J]. Journal of Optimization Theory and Applications, 2001, 110(3): 645-668.

[3] Antczak T. (p, r)−Invex sets and functions [J]. Journal of Mathematical Analysis and Applications, 2001, 263: 355-379.

[4] Yang X Q, Chen G Y. A class of nonconvex functions and pre-variational inequalities [J]. Journal of Mathematical Analysis and Applications, 1992, 169(2): 359-373.

[5] 焦合华. 半(p, r)−预不变凸函数[J]. 广西民族大学学报: 自然科学版, 2007, 13(1): 52-56.

[6] 王兴国. p−拟凸函数及其相关的几个问题[J]. 曲阜师范大学学报: 自然科学版, 2005, 31(1): 45-47.

Semi-p-prequasi-invexity Functions and Their Properties

WANG Xingguo

(Oujiang College, Wenzhou University, Wenzhou, China 325035)

Two classes of generalized quasi-invexity functions (p-prequasi-invexity fnctions and semi-pprequasi-invexity functions) were defined in this paper. Then some properties of the semi-p-prequasi-invexity functions were discussed. The results have wider scope of application than those of related articles.

Semi-p-invexity Set; Semi-(p,r)-pre-invexity Function; Semi-p-prequasi-invexity Function

O221.2

：A

：1674-3563(2010)04-0006-05

10.3875/j.issn.1674-3563.2010.04.002 本文的PDF文件可以从xuebao.wzu.edu.cn获得

(编辑：王一芳)

2009-12-22

王兴国(1968- )，男，浙江温岭人，副教授，硕士，研究方向：数学规划，数学教育