一种用于定性属性综合评判的属性重要性计算方法
伏明兰,陈吕强
(黄山学院信息工程学院,安徽黄山245021)
一种用于定性属性综合评判的属性重要性计算方法
伏明兰,陈吕强
(黄山学院信息工程学院,安徽黄山245021)
针对决策信息系统中一些属性的特性,即该属性的值不仅具有分类能力,同时也反映了其相对于决策属性的优劣,从而提出了一种综合权重的计算方法。首先根据模糊优属度的概念将定性属性定量化并对各属性进行归一化,然后计算各条件属性列向量相对于决策属性列向量的相关度。最后将相关度与粗集中属性重要性的评价方法相结合,得到有利于正确评价的综合权重计算方法,最后用实例证明了该方法的有效性。
粗糙集;综合权重;模糊优属度
1 引言
权重在进行综合评判或决策分析过程中至关重要,它反映了各个因素在综合评判和决策分析中所占有的地位或所起的作用,它直接影响到最终的评判和决策结果。
常用的权重确定或计算方法主要有专家评分、模糊统计、二元对比排序等,但它们在实际应用中都存在着明显的不足,它们都没有考虑到条件属性与决策属性之间内在的关联程度,因此有些学者采用基于粗糙集理论[1,2]的属性重要性来作为客观权重。[5]本文针对实际生活中广泛存在的一类决策信息系统的特点,即其属性为越大越优型属性或越小越优型属性,属性值不仅具有分类能力同时其值的大小也反映了它所代表对象的优劣。通过计算条件属性和决策属性的相关度,再结合粗集中属性权重的概念,提出一种用于综合评价的属性权重计算方法。
2 基本概念
定义1:称S=(U,A,V,F)是一个决策信息系统。其中U是非空有限论域,A=C∪d是属性集,C和D分别是条件属性集和决策属性。是属性值的集合,Va表示属性a∈A的值域,f:U×A→V是一个信息函数。任意的对象x∈U,对于任意属性a∈A,对象x在属性a上的取值为a(x)∈Va。
定义2:设S=(U,A,V,f)是一个决策信息系统,A=C∪d是属性集,决策属性d的决策等价类为,B为一个条件属性子集,则定义B对D的近似分类质量rB(D)为:

定义3:设B为条件属性全集,对于条件属性a(a∈B)在属性集B中的重要性定义为:

定义4:设决策信息系统S=(U,A,V,f),A=C∪d是属性集,C和d分别是条件属性集和决策属性,ai∈A为定性或定量属性,如果ai的值越大其所对应的对象的性能越好,则称该属性为越大越优型属性,反之,如果ai的值越小其所对应的对象的性能越好,则称该属性为越小越优型属性。
定性属性的程度及水平通常都是用模糊语言来描述的。比如描述某一事物的优劣程度用“很好,好,一般,差,很差”等模糊语言来刻划,这种描述没有严格的量的概念,为了能定量地表达和描述属性的程度及水平,并将越小越优型属性转化为越大越优型属性,下面引入模糊优属度的定义。
定义5[4]:某一事物或概念从属“优”这个模糊概念的程度,称为该事物或概念的模糊优属度,用r表示。
r是0到1之间的某一实数,它的大小即代表该事物的优劣程度。当r=1则该事物属于完全优,当r=0则该事物属于完全劣,r越接近1,则属于“优”的程度就越大。
在模糊集合论中,扎德提出许多确定隶属度的公式,其中,可用来判定优劣程度的隶属度公式如下(设决策信息系统S=(U,A,V,f),设ai(xj)为对象xj对应属性ai的属性值,对象个数为n,条件属性个数为m):
对于越大越优型属性ai,xj的优属度为:

其中,Sup(ai)=max(ai(xj))(j=1,2,…,n),
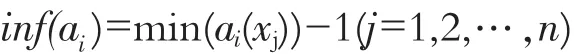
对于越小越优型属性ai,xj的优属度为:
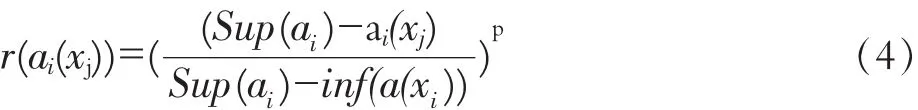
其中,Sup(ai)=max(ai(xj))+1(j=1,2,…,n),
inf(ai)=min(ai(xj))j=1,2,…,n,p为指数。一般取p=1,则优属度函数为线性函数。
定义6:设决策信息系统S=(U,A,V,f),S的每一列构成一个列向量,向量a表示条件属性a所对应对象的值,向量d则表示决策属性d所对应的属性值。向量a与向量d的夹角θ越小,0°≤θ≤180°,
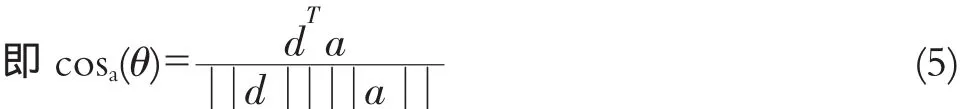
越大,属性a就相对重要。cosa(θ)反映了该属性值的大小对决策属性值的大小的决定作用。再将粗集中反映a分类能力的da(D)考虑进来,故定义属性a的综合权重为:

其中0≤u≤1为偏好系数。
3 属性综合权重计算步骤及实例分析
属性权重的计算分为4步,首先将定性属性定量化,再利用公式(3)或公式(4)计算各属性的优属度,即将其归一化。[5]然后利用公式(5)计算各条件属性对决策属性值的大小的决定作用,最后应用公式(6)计算各属性的综合权重。下面举一实例具体说明属性约简的方法。
设一决策信息系统汽车销售情况信息表S如表1所示。

表1 汽车销售情况信息表
首先将各属性定量化,设{豪华,普通}={2,1},{高,中,低}={3,2,1}。计算属性a1,a2,a3,d的模糊优属
度,其中a1,d是越大越优型属性,利用式(3)计算其优属度,其中inf(a1)=0,Sup(a)=2,inf(d)=0,Sup(d)=3,a2,a3为越小越优型属性,利用式(4)计算其优属度。其中inf(a2)=1,Sup(a2)=4,inf(a3)=1,Sup(a3)=4,于是得归一化后各对象新的属性值如表2所示。

表2 归一化后的决策表
然后根据式(5)计算cosa(θ)得:cosa1(θ)=0.8348,cosa2(θ)=0.8614,cosa3(θ)=0.8360,再根据式(2)计算dai(D):da1(D)=0,da2(D)=1/8=0.1250,da2(D)=3/8=0.3750,根据式(6)计算综合权重为:β(a1)=0.4172,β(a2)=0.4932,β(a3)=0.6055。其中设u=0.5。从cosa3(θ)的值最大可以看出耗油量的多少对销售量的高低的影响最大。da3(D)的值最大,可以看出a3的分类能力更强,但并不表明价格越低销售量就越高。β(ai)的值的大小综合两方面的评价标准得到属性相对更为重要。
4 结束语
本文针对实际生活中广泛存在的一类决策信息系统提出了一种综合权重的计算方法。该类系统中包含大量越大越优型属性或越小越优型属性,通过计算各属性值向量与决策属性值向量的相关性来计算各条件属性对决策属性的决定性,再与粗集中传统的属性重要性计算方法相结合从而使得到的综合权重更加合理,对汽车销售信息表的分析证明本文提出的方法有效。
[1]曾黄麟.粗集理论及其发展[M].重庆:重庆大学出版社,1998:10-52.
[2]曾黄麟.智能计算[M].重庆:重庆大学出版社,2004:2-40.
[3]李华,吴志强,王芸.基于属性重要性的Rough集属性约简方法[J].计算机与现代化,2006,13(6):69-70.
[4]孙惠琴,雄璋.基于粗集的模糊聚类方法和结构评估[J].复旦学报(自然科学版),2004,43(5):819-822.
[5]刘晨光,蒋水心.多目标优化中定性和定量属性的计量及归一化[J].郑州工学院学报,1990,11(3):87-95.
责任编辑:胡德明
Abstract:Based on a feature of some attributes in decision information system,that is,the value of an attribute not only has the ability of classification but also can reflect the optimal membership degree of the attribute with respect to decision attribute,a method of computing comprehensive weight is proposed.Firstly,the qualitative attribute is quantified and all other attributes are standardized.Secondly,the relevance between column vector of every condition attribute and decision attribute is computed.At last,by combining the relevance and the traditional weight assessment method in RS,a method of computing comprehensive attribute weight for correct evaluation is obtained.The effectiveness of the method is demonstrated by the application simulation.
Key words:rough sets;comprehensive weight;fuzzy optimal membership degree
A Method of Computing Attribute Weight for Comprehensive Estimation of Qualitative Attribute
Fu Minglan,Chen Luqiang
(School of Information Engineering,Huangshan University,Huangshan 245021,China)
TP310
A
1672-447X(2010)04-0013-03
2010-05-06
黄山学院自然科学研究项目(2008xkjq008;2010xkj012)
伏明兰(1981-),四川广元人,黄山学院信息工程学院教师,硕士,研究方向为粗集理论、信息系统。

