大斜度井中倾斜校正方法

桂彩云，白彦，孙永，马欢波

（西安石油大学 光电油气测井与检测教育部重点实验室，陕西 西安）

0 引言

斜井中的感应测井信号由于受井眼、侵入、围岩、倾斜以及趋肤效应影响，测量信号不能有效反映原状地层信息。其中，倾斜角的存在导致地层边界处围岩影响加剧，反映在测井曲线上，即井眼附近严重的尖峰或凸起以及不同阵列曲线幅度的分离，这在各向异性砂岩层中尤为明显，因此测量信号后处理时必须对异常信号进行校正。任何一个信号处理系统都包括信号的输入，系统函数和信号的输出3大部分，感应测井响应系统如图1所示。

图1 测井响应系统

从图1可以看出，测井响应作为整个系统的输出是地层属性、仪器特性和井眼环境的函数。地层属性是客观存在因素，因此系统函数决定了输出信号的质量。对上述系统函数的控制可以从以下两方面着手：一方面是对测井仪器特性的改善，即硬件方面的预防；另一方面是对井眼环境的校正，即利用软件对信号的后处理。

1 硬件方面的预防

从硬件方面来说，井斜控制主要是对钻井过程中井眼垂直度的控制，其实质是对弯曲钻柱的变形和受力进行控制的问题，即通过改变钻具钟摆力和钻压作用下的钻头偏斜力的大小和方向来达到改变井斜角大小的目的。目前，国内外钻井防斜技术归纳起来主要有[1]钟摆法井斜控制技术、刚性满眼钻具组合防斜技术、离心力防斜纠斜技术、利用钻具弯曲防斜纠斜技术、导向钻井防斜纠斜技术、复合钻进防斜技术及井下专用工具防斜纠斜技术等。这些技术对钻井过程中井眼倾斜起到一定的预防和控制作用。

2 软件方面的校正

随着计算机技术的发展，一些在硬件上难以实现的技术，可借助计算机软件实现。计算机强大的计算功能和丰富的算法为倾斜校正提供了基础。自1962年Moran和Kunz[2]认识到倾斜井破坏了边值问题的旋转对称性以来，学者们就不断地研究斜井中的响应特性和校正方法。

2.1 图版法

当用计算机模拟深感应测井响应时发现倾斜地层中心的视电导率受倾斜角影响非常严重，随着倾角的增加视电阻率减小，地层视厚度增加。为了从倾斜地层中获得真实电阻率，1987年Shen[3]等人提出了针对斜井做围岩校正的图版法，在忽略井眼和侵入影响的前提下，利用精确的电磁理论，选择倾斜角度和围岩电阻率与实际接近的校正图版，读取地层中心电阻率 Ra，认为 Ra即是地层真电阻率。这种方法能定量的得到厚层的中心电导率，但不能反映出薄层的真电导率。

2.2 滤波法

最早发展起来的滤波技术是三点反褶积法，用于直井信号的处理。后来Shen在研究倾斜校正时将直井中的三点反褶积加以改进，用于斜井中经图版法校正后的二次校正。虽然三点反褶积滤波只适用于线性系统，但是这种线性系统的假设，却成为许多滤波器设计的基础。1989年Barber和Howard[4]在线性理论的基础上，假设地层为阶跃模型，利用最小二乘法设计了对向量感应测井做倾斜校正的滤波器，但该运算法则使用范围小，只能用于无强烈井眼和倾入影响的向量测井信号处理，当倾角大于70°时非线性影响严重，滤波器失去了预期的效果。

感应测井以电磁场理论为基础，通过测量接收线圈的电压，从而求取电导率。对斜井中接收线圈电场强度的分析，得出倾斜响应包括：背景响应，电荷响应和体积响应。其中电荷项是造成倾斜影响的主要原因，因此在设计倾斜校正滤波器时可分开考虑，先设计针对主要影响做校正的滤波器，在此基础上再设计用于二次校正的滤波器。Xiao[5]等人正是利用此思想处理斜井中的响应信号，首先将地层简化成具有均匀电导率的上覆地层和下覆地层如图2所示。

图2 阶跃地层模型

从总的响应中分别提取电荷响应和体积项响应；然后利用带约束的最优化方法，采用二维滤波技术进行电荷影响校正 ；最后在电荷影响校正的基础上，再设计二维分辨率匹配滤波器做斜井中的体积影响校正。经过双重滤波处理后，围岩影响得到消除，地层边界处的尖峰值减小，不同阵列曲线幅度重合。校正后的信号与相同条件下的直井测量信号相比基本重合。但该方法依然以线性系统为前提，实际测井环境是非线性系统。为了克服非线性影响，Eddie[6]等人利用最小均方法，将不同的噪声源分开考虑，分别设计各自的滤波器，通过选择不同的窗函数，消除倾斜、倾入、围岩等影响，每个滤波器只能消除其中一种噪声源，繁冗的滤波器设计不利于实际处理。

Doll提出的几何因子理论是感应测井仪器信号处理的基础，可以用来准确描述地层各部分对测量信号的贡献。Sheng Fang[7]等人利用非正交坐标系，建立倾斜井眼中仪器轴和地层法线之间的角度关系，引进椭圆地层环的概念，并推导出斜井中几何因子的解析式。

该解析式能够反映斜井的响应特性，并大大简化了从地层中提取响应函数的过程。利用快速傅里叶变化设计的自适应滤波器能同时消除电荷和围岩的影响。这种以斜井几何因子解析式为基础的新的运算法则，在实际运用时收到了较好的效果，能够处理倾斜角高达75°的测量信号。

2.3 反演法

许多反演方法已被用于处理感应测井资料，斜井信号的处理主要用到了最大熵值反演法[8-10]和神经网络反演法[11]。最大熵值法是用连续模型代替参量模型，构建地层电导率的拉格朗函数：

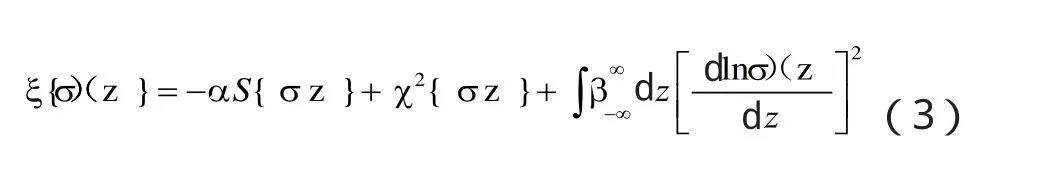
第一项是熵值，第二项的卡方估计描述了正演模型和测量数据之间的拟合程度，第三项是对数平滑项。最大熵值的原则是使拉格朗函数最小化，相当于解一个非线性最优化问题。利用拟牛顿法解该最优化问题，通过反复迭代，能够分别反演出一维、二维阵列感应原始数据，尤其适用于一维地层原始数据的反演。最大熵值法反演的结果，提高了测井数据的纵向分辨率和真电导率的准确性。其显著的优点是可用于任何倾角的校正，当给定的倾角太大或太小时，该方法能够给出明显的标记，但需要在不同的倾角之间多次运算最终做出决定。反复迭代以及雅克比矩阵的计算，需耗费大量时间，不利于现场的实时处理。

倾斜校正反演法的另一个主要方法是神经网络法，该方法是 20 世纪 90 年代发展起来的一种非线性处理技术，能够完成输入和输出之间复杂的非线性映射。神经网络算法在解决仪器响应和地层特性之间的复杂关系时有其独特的优越性，它利用给定的训练样本，在学习过程中，不断修正内部连接权重和阈值，使实际输出的电阻率与期望输出结果非常接近。训练过程中最重要的是选取一种能够确定最优网络连接参数的训练方法，通常选取LM（Levenberg- Marquardt ）算法。2001年San Martin[12]研究出了基于反卷积的神经网络算法，该算法将所有子阵列的接收数据分开处理，将测井响应作为多层前馈神经网络（MFNN）的输入，经过一个嵌套的传递函数，即神经网络系统，输出地层真电阻率。相比其它反卷积法，神经网络反卷积法能够很好地处理测井系统的非线性问题。但这种方法却存在反卷积的固有缺点，使得数值稳定性不能保证。

2.4 解析法

解析法是依据电磁场理论解层状介质中的Maxwell方程，由电压求地层电导率的方法。ADInn[13]测量是一种基于标准AIT测量发展起来的斜井测量法。19世纪60年代中期，Pierre Grimaldi解双线圈的Maxwell方程，对斜井中接收线圈的电压分别求发射位置ZT=hTcos和接收位置ZR=hRcos的导数，结果等于常量，解析式如下：

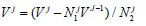
3 总结

倾斜校正的方法很多，硬件技术只能最大限度地对斜井进行预防，另外由于地质构造的原因，实际钻井时还存在地层倾斜的客观环境，这是硬件技术不能消除的。软件方面：由于实际测井环境的未知，具有自适应能力的二维滤波技术，是倾斜校正较为理想的处理方法，且实时处理速度快，但能校正的倾斜角度受到限制。

反演法适用于任何倾斜角度的校正，但要求相对倾角已知，通常情况下倾斜角是未知的，尤其是客观原因造成的地层和仪器的局部倾斜。该方法计算量大，耗时长，不利于实时处理。

解析法不受倾角给定的限制，理论上可以得到任何倾角下的地层电导率真值，但探测深度浅，只在具有浅浸入的油基泥浆钻井环境下得到很好的处理效果，因此只能作为现场处理的一种辅助方法。

综上，斜井校正的方法还需不断的完善和改进，利用解析不受角度限制的理论基础，设计非线性二维自适应滤波器，使得理论研究更具有适用性。

[1]王凤腾.国内外井斜控制技术的发展[J].内蒙古石油化工，2009(8).

[2]Moran J H，Kunz K S.Basic theory of induction longing and application to study of two-coil sondes[J].Geophysics，1962，27(6)：829-858.

[3]R.H.Hardman，L.C.Shen.Charts for Correcting Effects of Formation Dip and Hole Deviation on Induction Logs[J].The Log Analyst，July-AuguSt，1987.

[4]Barber，T.D.and Howard，A.Q.Correcting the induction for dip effect.Society of Petroleum Engineers[J].1989，in SPE 64th Annual Technical Conference Transactions.

[5]Xiao，J.Beard，D.and Zhou，Q.A pratical dippingeffect correction for MultiarrayInduction tools in Deviated wells[J].SPWLA 37th Annual Logging Symposium，1996，June 16-19.

[6]Eddie，P.and Todd ，E.Fisher.Induction log deconvolution for deviated boreholes[J]，SPWLA twenty-third annual logging symposium，July 6-9， 1982.

[7]Sheng Fang，Tsili Wang，and Ingo Geldmacher，M.Baker Atlas.Dipping-Effect Correction for the High-Definition Induction Logging Tool Using New Geometrical Factors[J].Society of Petroleum Engineers Inc，1999，3–6 October.

[8]Thomas.Barber，D.Tracy Broussard，Gerald，N.Interpretation of Multiarray Induction Logs in Invaded Formations at High Relative Dip Angles[J].SPWLA， 1999，39th Annual Logging Sy～iiposium，May 26-29.

[9]Gerald N.Maximum entropy inversion of induction-log data[J]，Society of Petroleum Engineers ，1991，Volume 6，Number 2.

[10]Gao，L.Halliburton Energy Services.Fast Induction-Log Inversion Using Quasi-Newton Update[J].Journal SPE Reservoir Evaluation & Engineering, 2003，6 (6)

[11]San Martin，L.Neural network inversion of array induction logging data for dipping beds[J].SPWLA，42th Annual Technical Conference and Exhibition，2001.

[12]丁柱，杨长春.神经网络反演双侧向电阻率测井曲线的物理约束[J].地球物理学进展，2002 ，17(2) .

[13]T.D.Barber，G.N.Minerbo，Schlumberger.An Analytic Method for Producing Multiarray Induction Logs That Are Free of Dip Effect，Society of Petroleum Engineers，2003, 6(5).