线性啁啾光纤Bragg光栅分段切趾优化

张 昊，陈书明

（1.福建师范大学 医学光电科学与技术教育部重点实验室，福建 福州 350007 2.福建金融职业技术学院，福建 福州 350007）

线性啁啾光纤Bragg光栅分段切趾优化

张 昊1，2，陈书明2

（1.福建师范大学 医学光电科学与技术教育部重点实验室，福建 福州 350007 2.福建金融职业技术学院，福建 福州 350007）

分段切趾是光纤光栅一种新的切趾改进技术。针对线性啁啾光纤Bragg分段切趾的两个重要参数：分段切趾比例和分段切趾强度进行讨论。基于数值模拟的结果，以三分段切趾为例，分析两个参数对光栅性能的影响以及进行优化的方法。

线性啁啾光纤Bragg光栅；分段切趾；切趾强度参量；半高宽；时延纹波振幅

1 引言

光纤光栅的切趾作为对光栅性能有着重要影响的参数，从出现伊始就得到学术界的重视和讨论[1,2]。近年来针对传统单一函数完全切趾的种种不足之处，不少新的切趾技术被提出，如部分切趾、不对称切趾等等[3,4]。而分段切趾作为部分切趾更特殊的情况，近年来也得到了讨论[5]。切趾优化是切趾技术的一个重要的讨论内容，对于单一函数完全切趾的优化问题，前人已经做出了众多的研究[6～9]，这里将针对光纤Bragg光栅分段切趾的优化问题进行分析。

由于光纤光栅拥有众多的可控参数，这些参数的变化都会对光栅的性能造成影响，因此在讨论切趾优化的时候，需要把一些与切趾优化问题关系不大的参数进行事先选定。文章后面进行的讨论都是在光栅的长度、光栅周期、啁啾系数、背景折射率以及折射率调制深度固定的情况下进行的，所采用的切趾函数形式也定为常见的高斯型切趾。文章重点分析分段切趾的控制参数对切趾性能的影响。下面，先引入分段切趾中两个重要的参数。

2 分段切趾比例和分段切趾强度参量

分段切趾是将整个光栅划分为K个的分段，根据实际的需求，不同的分段采用不同的切趾函数，因此可以定义每段的切趾比例参量为[5]：

其中Liad表示第i段的切趾长度。本文以三分段切趾的光纤光栅作为讨论的对象，在对称的前提下，只需要考虑中间分段的切趾比例AM=即可。

切趾强度参量（也称为切趾锐度参量，Apodisation Sharpness Factor）是对切趾效果的强弱进行定量描述的参量，是光纤光栅的切趾分析中的一个重要参数，可以由下式表示[6,7]：

L为光栅长度，Ta为光栅的切趾函数。针对分段切趾中每段所采用的切趾函数形式不同，相应可以定义每段切趾强度参数的表达式为：

其中Tia为第i段切趾函数。则整个光栅上的切趾强度参数的表达修正为：

3 分段切趾比例对光栅性能的影响

取光栅长为2 cm，中心Bragg波长1550 nm，背景折射率1.447，折射率调制深度0.0003，线性啁啾参量0.003，采用转移矩阵法进行数值模拟分析，转移矩阵的分段数为100（本文后面的讨论都基于同一根光栅）。采用3分段切趾，两侧和中央的切趾函数分别为：

a1、a2为不同部分高斯函数的控制参数，为了保证切趾函数为钟型，a1≤a2。取不同中段切趾比例AM为30%、50%、70%，得到的反射谱和时延情况如图1所示：

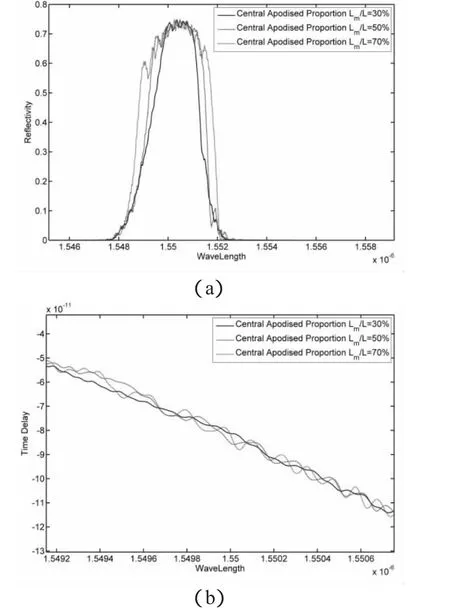
图1

从中可以看到，随着中央部分的切趾比例的增大反射谱的谱宽也随着增大，同时时延的纹波也加大，图2分别描绘了中央部分采用不同的切趾函数切趾时，反射谱的半高宽（FWHM）和半高宽内的平均时延纹波振幅（MTDRA）随中央切趾比例的变化情况。

图2

可以看到随着中央切趾比例的增加，整个反射谱的半高宽和平均时延纹波振幅都是加速上升的，当中央切趾比例小于40%之后，半高宽和平均时延纹波振幅都趋于平稳，综合考虑，中央部分切趾占40%是比较合适的比例，这也符合所谓的切趾黄金比例[4]。

4 分段切趾强度参量对光栅性能的影响

在光纤光栅的结构中，不同位置的光栅周期不同，对应在反射谱上不同波长的部分，因此不同位置切趾情况的变化也会造成反射谱上相应位置的变化。下面通过改变光栅不同部分的切趾函数的切趾强度，来分析不同部分的切趾强度变化对光栅性能的影响。

对三分段切趾的光栅只要考虑两侧和中央两种情况的变化，在本文中固定切趾函数为高斯型Ta=exp通过改变控制参数a来实现对切趾强度的变化。首先，固定中央的切趾函数，改变两侧的切趾函数的参数，得到的反射谱和时延变化情况如图3所示：

图3

可以看到随两侧切趾控制参数a的增大，反射谱趋于平滑，同时半高宽减小，时延纹波也随之减小。可以画出不同的中央切趾比例下，两侧切趾强度的变化时,反射谱的半高宽以及半高宽内平均时延纹波振幅的变化如图4所示：

图4

随着切趾强度参量的增大，反射谱的半高宽逐步增大图中虚线是完全切趾时半高宽的变化情况。时延纹波也随切趾强度参量的增大而增大。再固定两侧的切趾函数，改变中央的切趾函数的控制参数，得到的结果如图5所示：

可以看到改变中央部分的切趾强度，对反射谱宽和时延纹波的影响都远小于改变两侧的切趾强度。这是由于光纤光栅所选择的切趾函数都是钟形，因此中央部分切趾强度的改变量远小于两侧。同样也可以画出反射谱的半高宽以及半高宽内平均时延纹波振幅随中央切趾强度的变化情况，如图6所示。

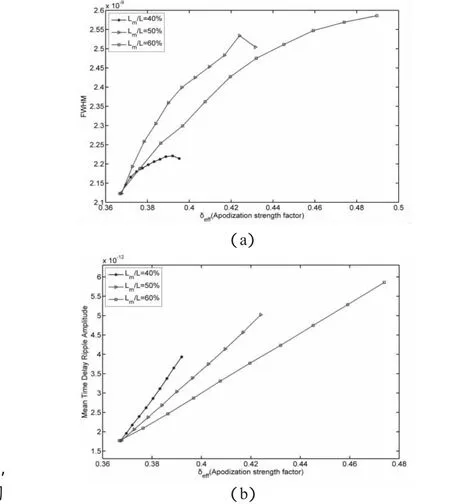
图6

在相同的整体切趾强度改变量下，可以绘出改变两侧和改变中央切趾强度对平均时延纹波振幅的影响对比，如图7所示：

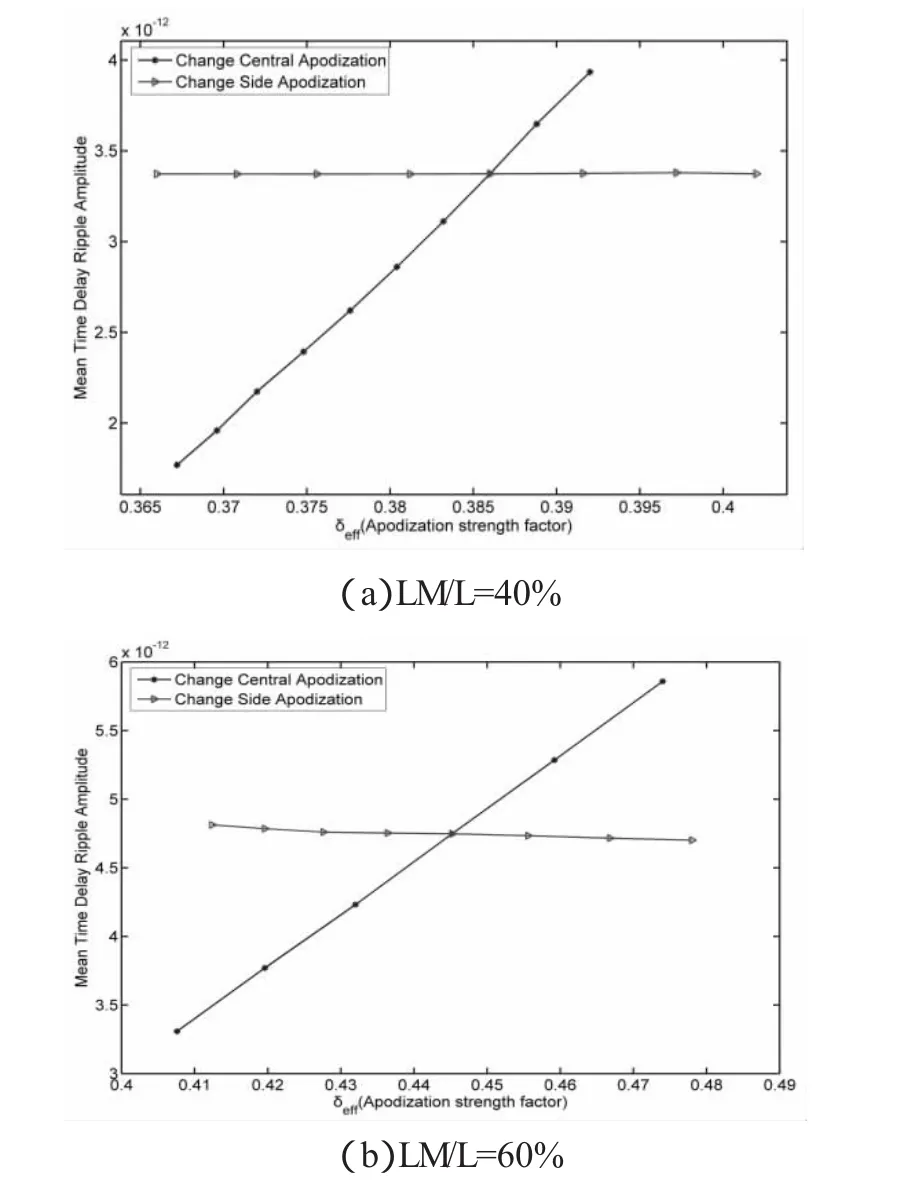
图7

从图7容易看到，对于整体切趾强度相同的情况下，改变两侧的切趾强度参量对平均时延纹波振幅的影响比改变中央的切趾强度参量的影响小。也就是说，在允许的范围内，减小光栅中央部分的切趾强度参量对时延纹波的抑制作用将比减小光栅两侧的切趾强度参量对时延纹的抑制更明显。同时，从图（3-a）与（5-a）的对比不难看出，减小中央的切趾强度参量对反射谱谱宽的影响更小，因此得以尽可能在保证谱宽不变的同时抑制时延纹波。

5 结束语

文章分析分段切趾中两个重要的控制参数——分段切趾比例和分段切趾强度——对光纤光栅的反射谱和时延曲线的影响。丛中可以看到：分段切趾比例主要决定反射谱的半高宽，随中央部分的切趾比例的增加，半高宽和时延纹波都会快速增大，如果要兼顾半高宽和时延纹波，40%左右的中央切趾比例是一个比较合适的选择；而分段切趾强度对谱宽和时延纹波的影响体现在，切趾强度的减小会减小反射谱的半高宽，而在一定的范围内，减小光栅中央部分的切趾强度参量对时延纹波的抑制作用比减少光栅两侧的切趾强度参量作用大，这是一个很有意义的现象，可以作为优化反射谱宽与时延纹波关系的一种方法。

［1］Malo B．Theriault S．Johnson D C et al．Apodised In-Fibre Bragg Grating Reflectors Photoimprinted Using a Phase Mask［J］．Electronics Letters，1995，31：223-225.

［2］Turan Erdogan．Fiber Grating Spectra ［J］．Journal of Lightwave Technology，1997，15（8）：1277-1294.

［3］Zervas MN，Taverner D．Asymmetrically Apodized Linearly Chirped Fiber Bragg Gratings for Efficient Pulse Compression ［J］．Fiber and Integrated Optics,2000，19（4）：355-365.

［4］王琳，延凤平，等.非对称切趾对啁啾光纤光栅特性优化的分析［J］.光学学报，2007，27（4）：587-592.

［5］张昊.线性啁啾光纤Bragg光栅的分段切趾技术［J］.洛阳理工学院学报（自然科学版），2009，19（1）：87-91.

［6］Ennser K．OptiMization of Apodized Linearly Chirped Fiber Gratings for Optical Communi-cations［J］．Journal QuantuMElectronics，1998，34：770-778.

［7］P Fern?ndez，JC Aguado，JBlas et al．Analysis and Optimisation of the Apodisation Sharpness for Linearly Chirped Dispersion Compensating Gratings［J］．IEEE Proc.Optoelectron，2004，151（2）：69-73.

［8］Jozef Ciosmak，Marian Marciniak．Impact of Apodisation on Fiber Bragg Grating Reflection and Phase Responses［J］．ICTON，2001，（W e.P.19）：287-290.

［9］胡海英，陈鹤鸣.用于色散补偿的线性啁啾光纤光栅的最佳切趾包络函数的研究［J］.南京邮电学院学报（自然科学版），2001，21（1）：23-27.

Abstract:Segmental apodization method is a new technology to improve the effect of apodized fiber gratings.Thisarticle analyses the apodization proportion and the apodization sharpness factor of piecewise apodized linearly chirped fiber Bragg gratings with a example of tri-segment symmetrical apodised grating based on the numerical result.The conclusion of analysis show how to optimize piecewise apodized linear chirped fiber Bragg gratings.

Keywords:linearly chirped fiber Bragg grating；segmental apodization；apodization sharpness factor；full width halfmaximum（FWHM）；time delay ripple amplitude

（责任编辑 王璟琳）

OptiMization of Piecew ise Apodized Linearly Chirped Fiber Bragg Gratings

ZHANG Hao1,2，CHEN Shu-ming2
（1.Key Laboratory of Optoelectronic Science and Technology for Medicine Ministry of Education，Fujian Normal University，2.Fujian College of Financial Techology，Fuzhou，Fujian 350007）

TP212

A< class="emphasis_bold">文章编号：1

1673-2014（2010）02-0004-04

2010—03—05

张 昊（1981— ），男，福建建瓯人，硕士，工程师，主要研究方向为光纤与光纤通信。