XML文档数对序列模型与结构相似度算法研究

苏慧群

(湖南师范大学树达学院，湖南长沙410012)

XML文档数对序列模型与结构相似度算法研究

苏慧群*

(湖南师范大学树达学院，湖南长沙410012)

为了更快更有效地计算XML文档之间的结构相似度，本文提出了一种新的数学模型——数对序列模型，同时在这个模型基础上改进了传统树模型的动态规划算法，并提出了一个新的更有效的算法——CA算法。实验证明，与传统方法相比，这个算法无论在最后的准确率、召回率还是时空复杂度上都有明显的改进。

XML;数对序列模型;相似度;算法

随着Web网上信息的爆炸增长，研究半结构化文档(特别是HTML和XML文档)相似度计算的问题变得越来越重要，尤其是在信息抽取、文档聚类与信息检索领域里，文档相似度计算起了极其重要的支撑作用。本文提出了一种新的模型——数对序列模型，用于解决传统算法和树编辑距离算法时空复杂度过高的问题。在数对序列模型的基础上，本文又提出多种计算XML文档结构相似度的算法，并进行比较研究。实验结果表明，本文的方法更显著地提高了识别具有先同结构的XML文档的能力，并且对文档有很好的聚类效果。

1 数对序列模型

1.1 基本定义

1.1.1 数对序列的基本描述

定义1.1结点位置信息:在一个森林S中，不妨设这个森林有n棵树依次为:T1，T2，…，Tn，一个结点x，若其不为树的根结点，x是其父结点的第m个孩子，则结点x的位置信息为m，记seat(x)=m，如果结点x为森林S第i棵树的根结点，则结点x的位置信息为i，记seat(x)=i。

定义1.2路径位置信息:设P为树T一条从根结点到叶结点的路径，P上所有结点依次为n1，n2，…，nd，d(d≥0)为结点个数，则P路径位置信息定义为一组序列，记为:seat(p)=seat(n1)，seat(n2)，…，seat(nd)。

有了上述定义，我们就可以通过增加路径位置信息来改进传统的树路径模型，我们称这个模型为树路径位置信息模型。

定义1.3树路径位置信息模型:设一个XML文档x，其对应的森林为S，并且S上所有从根结点到叶结点的路径从左到右依次为:P1，P2，…，Pn(n表示路径总数)。则我们称下式为文档x的树路径位置信息模型。

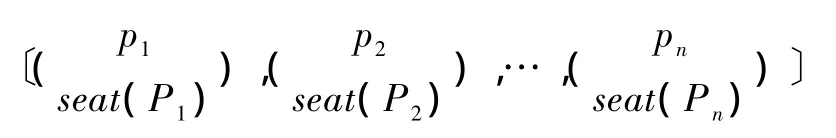
定义1.4变量α编码:变量α编码是指对一个变量所有可能性值的集合到集合{m|m∈N∧0≤m≤2α}的映射，此映射记作codeα，某个具体可能值x的具体编码值可记为codeα(x)，α表示的是编码因子。

显然，由定义1.1和定义1.2易知结点的位置信息和结点的具体值范围非常大，我们可以将其映射到一个较小的范围内，从而降低计算机存储代价。比如，我们取α为16，则编码范围只有［0，4095］，此时如果有一个结点有多于4096个子结点，则必然有两个子结点编码相同。也许，读者会认为编码相同会导致计算结果有误差，不过当α取值较大时，这种误差几乎可以忽略不计，原因是在现实的XML文档中很少会出现有很多个结点的子结点数都非常大的情况，就算出现这种情况，也不会对最终相似度计算结果有多大影响。

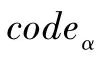
定义1.6序列α编码量大小:α编码量大小其实表示的是一个序列变量的个数，设u为一个codeα编码值，则u的α编码量大小为sizeα(u)=(log2u)/α。

定义1.7序列α解码:给定一个序列的α编码值，求解出这个序列所有变量的编码序列，为这个序列α解码，记为decodeα，一个具体编码值v的α解码为decodeα(v)。显然decodeα(v)为一个序列，第i个元素值记作decodeα(v)［i］，由定义1.4可知:decodeα(v)［i］=⌊v/2α(i-1)」%(2α)其中⌊」表示取下整，m%n表示是m整除n后的余数。

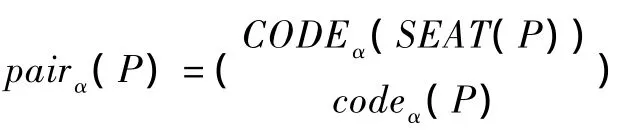
定义1.9 α数对序列:设S为一个森林，S的所有从根结点到叶结点的路径从左到右依次设为p1，p2，…，pi;l(l≥0)为路径个数，则森林S的α数对序列pairsα(T)=(y1，y2，…，yl)，其中y1=pairα(p1)，1＜j＜l。

上述定义，给出了一个森林(可以是XML文档的DOM树)的数对序列描述，数对序列是有多个自然数对序列成，因此在实际计算中，计算代价会大大减少。

那么如何计算一棵树的数对序列呢?实际上计算一棵树的数对序列很简单，只需先遍历这棵树的所有结点，计算出所有结点的位置信息，然后在计算出路径位置信息以及路径，再根据α编码分别求出所有路径对应的数对，从而得到这棵树的数对序列，显然时间复杂度为O(|T|)，|T|表示这棵树的结点数。如果要计算两个XML文档的结构相似度，只需计算这两个文档数对序列的相似度即可。

定义1.10数对序列模型:数对序列模型是一个三元组∏=(α，code，valueweight)，其中α为编码因子，code是编码规则，valueweight(0≤valueweight≤1)是数对计算过程中第二个自然数所占的权重。

1.1.2 数对序列的基本操作

与树模型相似的是，本文也对数对序列定义了三组最基本的操作Delete，Update，Insert。定义这三个基本操作之前，首先定义两个权值seatweight、valueweight和一个更基本的函数Common，其中seatweight表示位置权重，valueweight表示值权重，这两个权重满足seatweight+valueweight=1

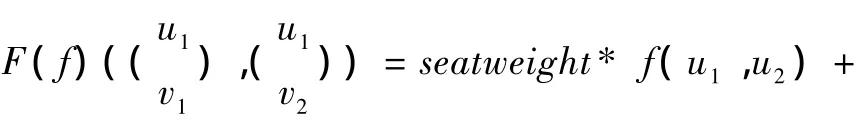
定义1.13最前公共最前子序列与Common值:设两个序列P1和P2，P1的序列为n1，n2，…，nl，P2的序列为，则P1和P2的最前公共子序列为n1，n2，…，nr其中r是指使等式都成立的最大的i，同时r即为这两个序列的Common值，记为。

定义1.14自然数n1，n2的α Common值:是指将自然数n1，n2进行α解码后得到两个序列的Common值。Commonα(n1，n2)=Common(decodeα(n1)，decodeα(n2))。

定理1.2自然数n1，n2的α Common值可以用以下公式求得:

Commonα(n1，n2)=⌊f(|n1-n2|)/α」，其中f(x)表示x二进制式末尾0的个数，例如f(1010100000B)=5。证明比较简单略。

定理1.3数对α Common值定理

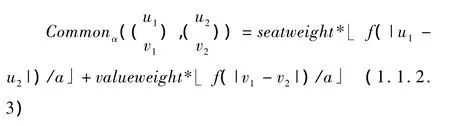
有了最基本的Common操作后，下面定义三个基本操作，Delete，Insert，Update。

定义1.15序列P1和P2的Delete值:表示序列P1转换为P1和P2最前公共最前子序列，所需的删除元素(变量)数，显然Delete(p1，p2)=size(p1)-Common(p1，p2)。(1.1.2.4)

定义1.16序列P1和P2的Insert值:表示P1和P2最前公共最前子序列转化为P2所需的增加元素(变量)数，显然Insert(P1，P2)=size(P2)-Common(P1，P2)。(1.1.2.5)

定义1.17序列P1和P2的Update值:Update(p1，p2)=Delete(p1，p2)+Insert(p1，p2)。(1.1.2.6)

根据1.11同理可以定义自然数和数对α Delete，Insert，Update值，具体计算方法为:

1.2 CA算法

在本节中，本文提出了CA算法，进一步提高了计算效率，查全率与查准率。

算法:μ逐对比较β衰减算法(CA算法)

目的:计算两个数对序列的相似度

输入:P=(p1，p2，…，pm)，Q=(q1，q2，…，qn)，衰减因子β(0≤β≤1)，步长μ(表示要寻找匹配范围的大小)，前进因子λ((0≤λ≤1))(用于根据被匹配的下标计算出具体寻找匹配的范围)。

上述算法时间复杂度大大减低，仅为O(μ(m+n))其中μ为步长因子，即每次寻找匹配范围的大小。如果将其应用到求解两个XML文档的相似度，则时间复杂度为O(|T1|+|T2|+μ(L1+L2))，L1，L2分别为XML文档转换为DOM树的叶子个数，大大低于树模型的时间复杂度O(|T1||T2|min(|D1|，|L1|)min(|D2|，|L2|)。

2 实验与结论

数对模型的CA算法有多个参数:编码因子α，衰减因子β，步长μ，前进因子λ，还有valueweight(注seatweight=1-valueweight)，下面我们用实验研究一下，这几个参数对准确率和召回率的影响。不妨这些参数的默认值为:α=2，β=0.8，μ=20，λ=0.8，valueweight=0.5。

从图2.1可以看出，衰减因子过小或过大，结果均不理想，在0.8到0.9之间比较合理。

从表2.1可以看出，步长取值太小，会影响召回率，太大又会增加时间消耗。

从图2.2可以看出，前进率取0.7到0.8是比较合理的选择。

可以看出，准确度随valueweight增大而减小，而召回率确恰恰相反，为取得一个综合性较好的结果，valueweight取0.5至0.8是个比较合理的选择。

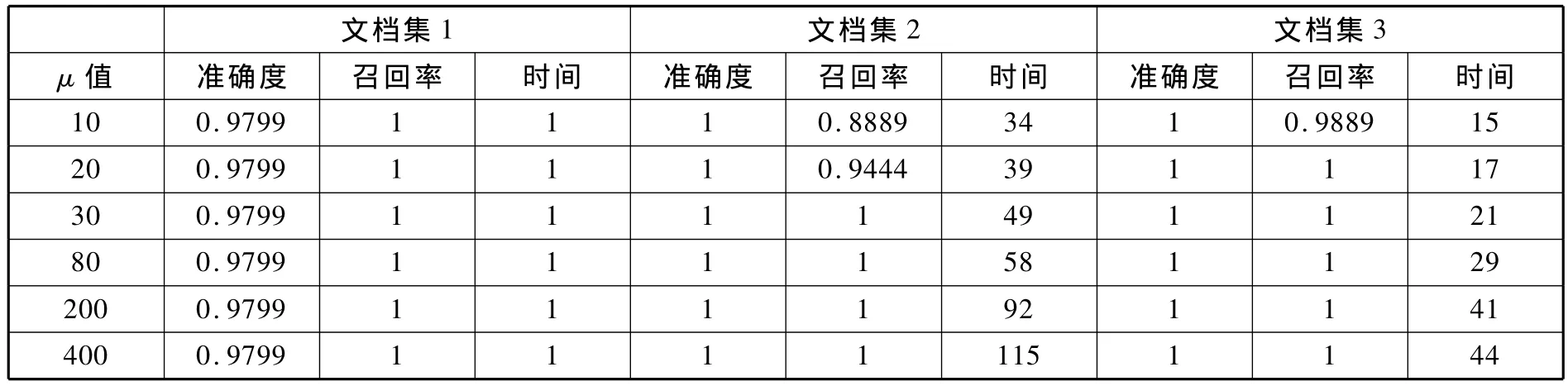
表2.1 步长μ对结果的影响

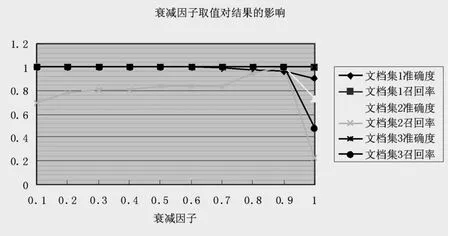
图2.1 衰减因子取值对结果的影响

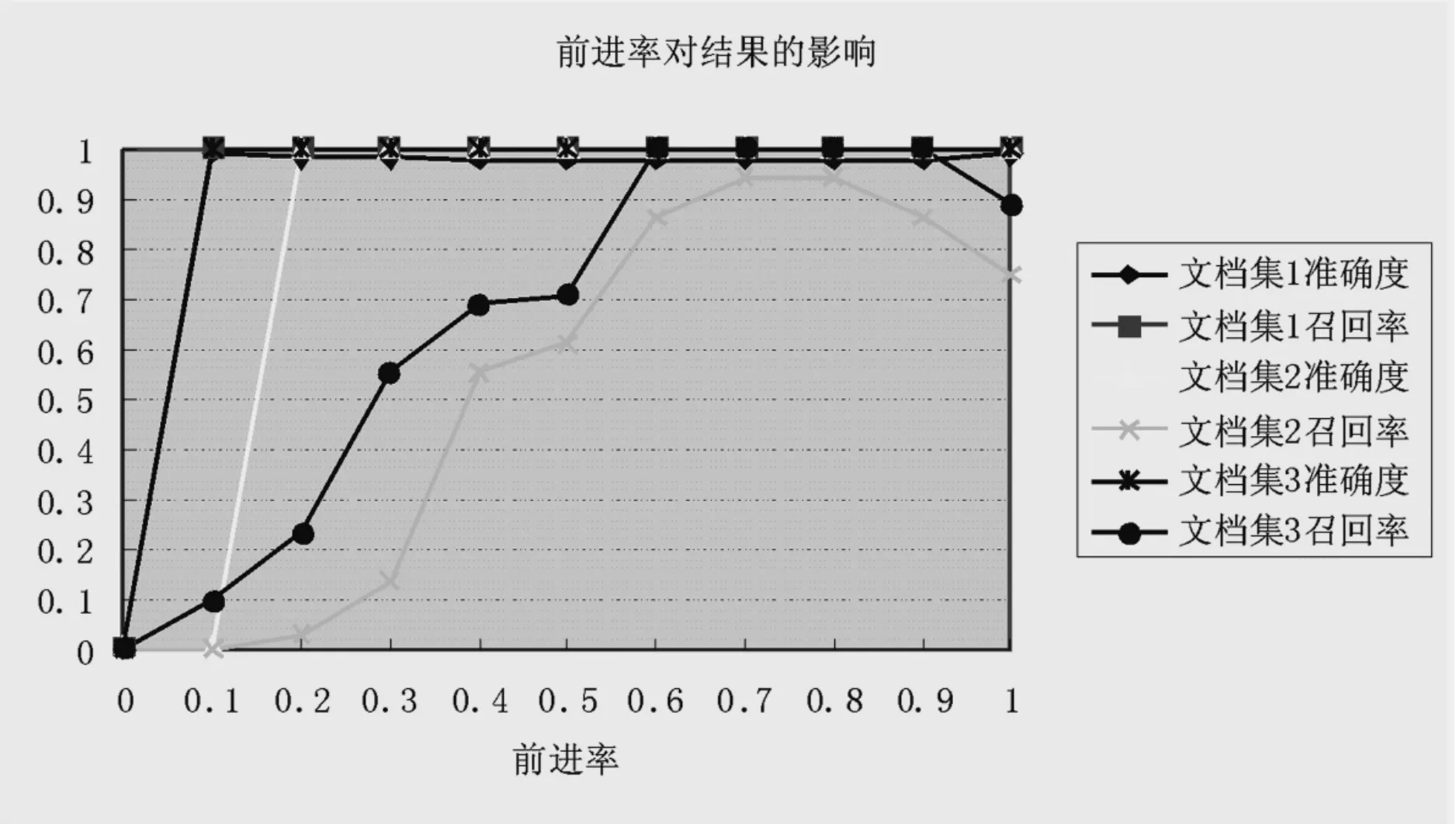
图2.2 前进率对结果的影响

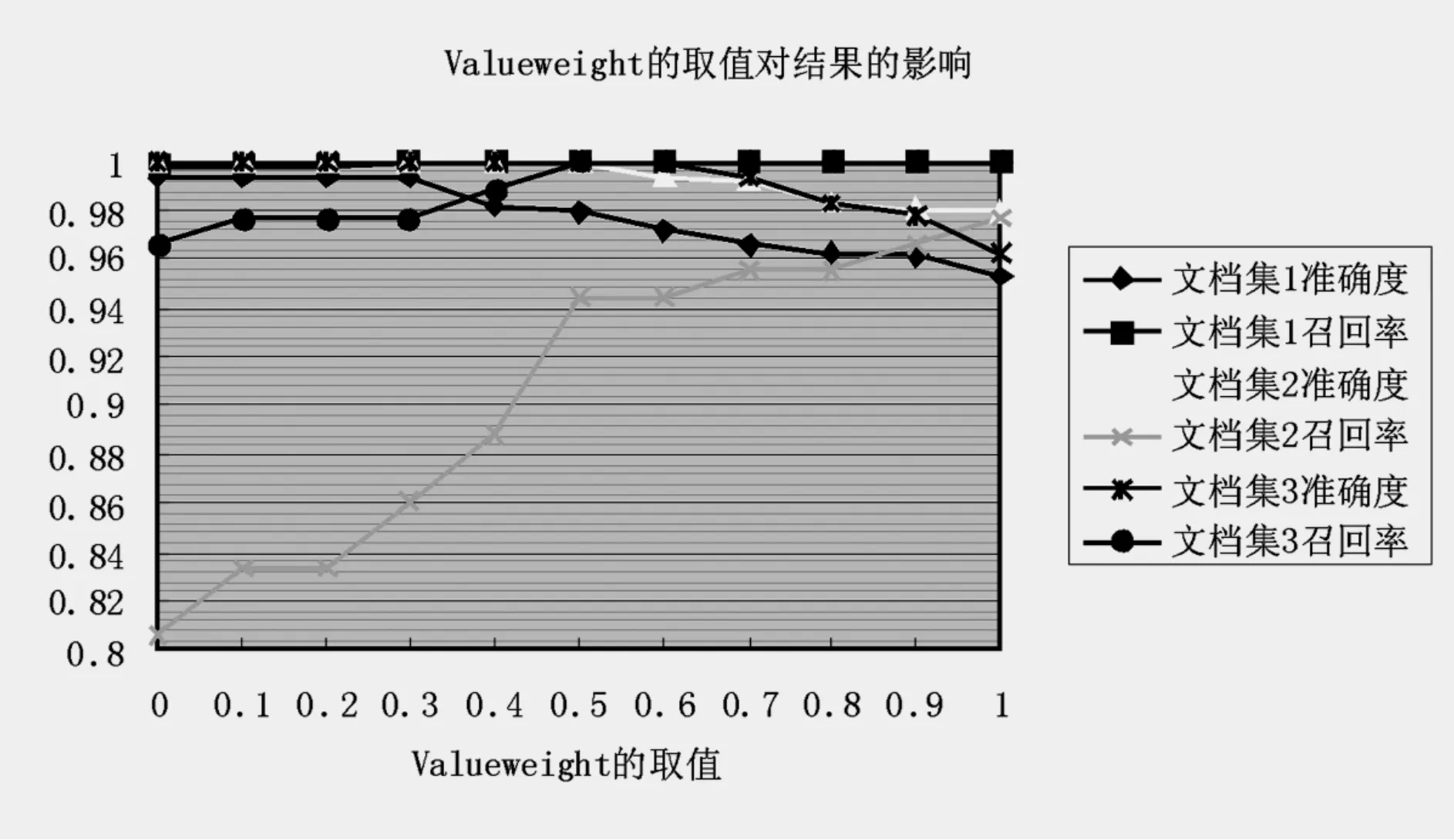
图2.3 取值对结果的影响

3 结束语

本文提出了一个优化的新模型——数对序列模型，同时给出一个更有效的新算法——CA算法。数对序列模型与CA算法解决了传统算法时间复杂较高、重复结点未被考虑、兄弟结点信息丢失的问题。再者，数对序列模型通过数字化编码，降低了时空开销，提高了存储计算效率。实验结果表明，新模型与新算法在准确率与召回率上也均有所提高。当然，在数对序列模型下有没有计算XML相似度更快更有效的算法，是值得我们以后再做进一步的研究与探索的问题。

［1］孙建军，成颖等.信息检索技术［M］.北京:科学出版社，2004.

［2］Monika Henzinger.“Finding Near-Duplicate Web Pagess:A Large-Scale Evaluation of Algorithms”.In the Proceeding of ACM SIGIR Conference，pages 284-291，2006.

［3］Zheng Chen，Wei-Ying Ma，Jinwen Ma.Learning to Cluster Web Search Results［A］.In proceeding of the 27th Annual International ACM SIGIR Conference［C］.Sheffield，South Yorkshire，UK，July 2004，210-217.

［4］Sachindra Joshi，Neeraj Agrawal，Raghu Krishnapuram and Sumit Negi.A Bag of Paths Model for Measuring Structural Similarity in Web Documents.SIGKDD＇03，August 24-27，2003.

［5］Prasanna Ganesan，Hector Garcia-Molina and Jennifer Widom Exploiting Hierarchical Domain Structure to Compute Similarity.ACM Transaction on Information Systems.Jan，2003.

［6］Braha D，Elovici Y，Last M.A theory of actionable data mining with application to semiconductor manufacturing control［J］.International Journal of Production Research，2007，45(13):3059-3084.

Abstract:In order to get the computation among the XML document faster and efficient，this paper mentioned a new mathematical model of sequence number the model based on improved traditional model of dynamic programming algorithm，and proposes a new algorithm is more effective-CA algorithm.Experiment proves，compared with traditional methods，this algorithm in the accuracy，recalling rate or space complexity significantly improved.

Key words:XML，model，similarity，algorithm

XML Sequence Model and Similarity Structure Algorithm

SHU Hui-qun

TP311.132

A

1009-5152(2010)03-0079-06

2010-06-09

苏慧群(1979-)，女，湖南师范大学树达学院助教。