锚杆多种失效模式与双滑块边坡锚固系统可靠性分析

陈昌富，成晓炜

(湖南大学岩土工程研究所，湖南长沙 410082)

锚杆多种失效模式与双滑块边坡锚固系统可靠性分析

陈昌富，成晓炜

(湖南大学岩土工程研究所，湖南长沙 410082)

考虑锚杆拉杆拉断、拉杆从注浆体中拔出、锚固段注浆体从岩体中拔出、外锚头破坏以及垫墩底岩体的压坏等失效模式，利用系统可靠性原理和极限平衡分析方法，建立了双滑块边坡多锚杆锚固系统可靠性分析模型。基于蒙特卡罗随机抽样原理提出了该类边坡锚固系统破坏概率的直接求解方法。最后结合算例，分别基于中值安全系数和破坏概率指标分析了各计算参数对计算结果的影响，并讨论了锚杆锚固角和被动滑块可能滑裂面倾角对锚固系统稳定性的影响。

边坡工程;岩质边坡;锚固系统;失效概率;系统可靠度;最优锚固角

0 引言

目前，可靠度理论已经广泛应用于边坡稳定性分析中，如:H.S.B.Duzgun等［1］研究了基于可靠度岩质边坡平面滑动破坏时的设计方法;陈昌富、王贻荪和邹银生［2］提出了一种计算边坡最小可靠性指标和搜索临界滑动面的分步混合遗传算法;张兴和廖国华［3］采用蒙特卡罗方法计算了多滑面边坡体系可靠度;吴震宇等［4］采用Ditlevsen窄界限公式估算了岩质边坡各失稳模式组成的串联体系可靠指标;李典庆等［5］以概率故障树模型考虑了多失效模式相关的岩质边坡平面滑动体系;但未见针对锚杆多失效模式的分析和研究成果的文献报道。

在锚固边坡优化方面，许多学者也做过很多工作，已经有很多的成果，比如，陈昌富［6］等人基于含有主控弱面双滑动破坏边坡的可靠度进行了优化分析;张发明等［7］应用优化与决策分析的理论对岩质边坡预应力锚索进行了优化设计与分析;熊文林等［8］考虑了坡面与滑面倾角的影响，对预应力锚索方向角进行了优化计算。但以上学者也没有对锚固系统服役期间的稳定性进行分析。

本文将锚杆本身多种可能的破坏模式考虑到整个锚固系统中去，建立了新的双滑块岩质边坡锚固系统可靠性分析模型，提出了基于蒙特卡罗法的此类边坡可靠性分析计算方法，同时以破坏概率为目标函数寻求锚杆最优锚固角和锚固系统的最危险滑裂面位置。

1 锚固系统的模型分析

1.1 锚杆多种破坏模式及系统模型

锚杆经常出现的破坏形式有［9］:(1)孔壁与注浆体结合面滑移破坏;(2)注浆体与钢筋结合面滑移破坏;(3)锚杆在自由段的钢筋拉断破坏;

如果外锚头用的是混凝土垫墩，并利用螺杆螺母锁定，那么此外还有如下几种破坏形式:(4)锚头垫墩底面下岩体被压碎;(5)外锚头处螺纹牙的剪切破坏［10］;(6)外锚头螺纹段最危险截面发生拉断破坏［10］;(7)外锚头处螺纹牙的受弯破坏［10］。

如果称上述每种破坏形式为一个事件，则单根锚杆是否正常工作取于以上各事件的工作情况。只要有一个事件发生，那么意味着这根锚杆失效。如果假设以上各事件是相互独立的，那么单根锚杆就可以看成由7个事件组成的串联结构模型。

假设边坡有n排锚杆，且锚杆间是相互独立的，那么岩质边坡锚固系统就可以看成是一个以含有多种破坏模式的锚杆为子系统的并－串联系统结构，如图1所示。图中Aji(其中，i=1，2，…，7;j=1，2，…，n)为第j排锚杆第i种破坏事件。

1.2 锚杆各破坏模式中的抗力分析

1.2.1 锚固段注浆体沿钻孔壁滑移破坏模式

此破坏模式的抗力函数表示为:

式中:D——注浆体直径(m);

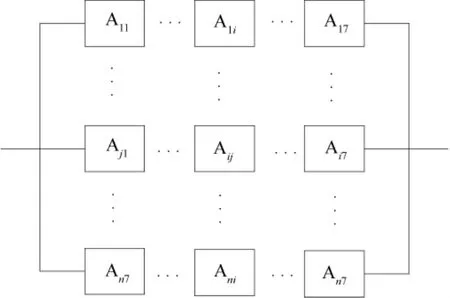
图1 锚固系统模型图Fig.1 Anchorage system model

qs——注浆体表面与周围岩土体间的粘结强度

(kPa); Laj——锚固段长度(m);

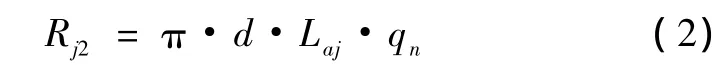
1.2.2 注浆体与钢筋结合面破坏模式此破坏模式的抗力函数表示为:式中:qn——注浆体与钢筋间的粘结强度(kPa); d——钢筋的直径(m)。

1.2.3 自由段钢筋屈服破坏模式

此破坏模式的抗力函数表示为:

式中:ft——钢筋的抗拉强度(kPa)。

1.2.4 锚头垫墩底面岩体被压碎破坏模式

这种破坏模式的抗力是由垫墩底面一定范围内的岩体的极限承载力来决定，岩体简化模型如图2所示。

由于坡面上的垫墩周围没有超载情况，垫墩没有埋深，所以不考虑坡面超载的情况，也无需进行深度修正，且不考虑重度的影响。假设边坡面为水平面，边坡面的法线为垂直面。基于太沙基理论［11］，垫墩底面下岩层能够提供的极限承载力表示为:

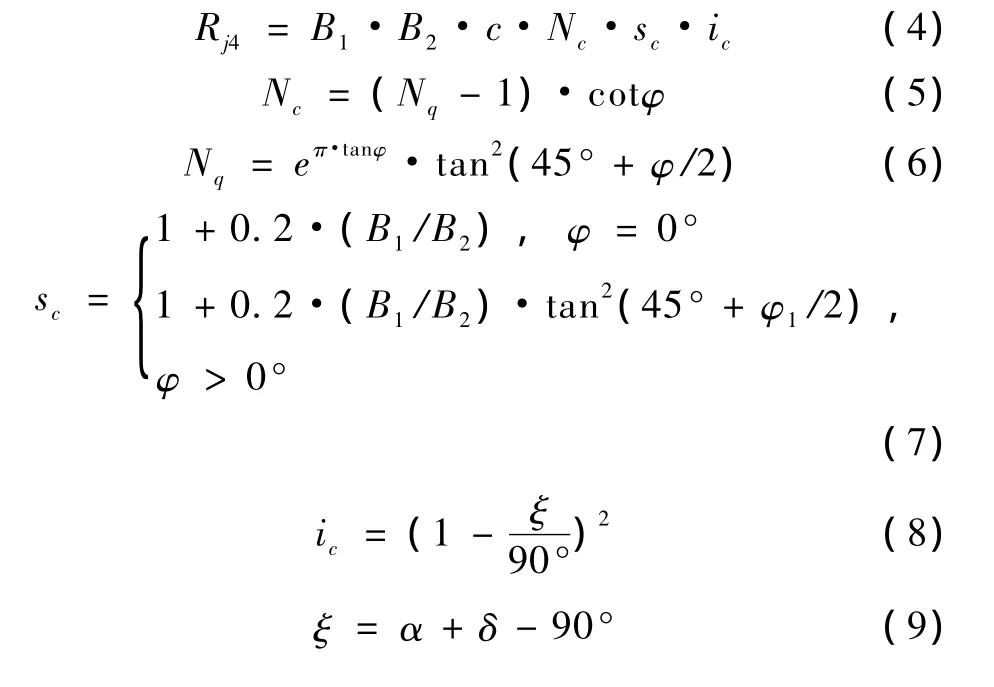
图2 垫墩底岩体被压坏的模型图Fig.2 Model for failure of rock below pad pilla

式中:B1、B2——垫墩底宽度(m)和长度(m);

Nq、Nc——承载力系数;

c、φ——滑块岩体的粘聚力(kPa)和内摩角(°);

sc、ic——粘聚力c的修正系数;

ξ——锚拉力与坡面法线的夹角(°);

δ——锚杆与水平面的夹角，即锚杆的倾角;α为边坡倾角(°)。

1.2.5 外锚头处螺纹牙剪切破坏模式

假定螺纹只受轴向力而不受径向力，螺纹各工作圈之间载荷均匀分配并且内外螺纹之间没有间隙［10］。那么此破坏模式的抗力函数为:

式中:τ——螺纹牙的抗剪强度(kPa);

d1——螺纹端盘螺纹内径，对于公制基本三角形螺纹标准［10］，d1=0.83d(d为锚杆钢筋直径，m);

B——断面处齿根宽度，对于公制基本三角形螺纹标准，B=0.872P(P为螺距);

z——工作螺纹牙数，z=L/P;L为外锚头螺丝端杆螺纹的螺合段长度，一般等于螺母高度(m)。

1.2.6 外锚头处螺纹牙弯曲破坏模式

把旋合段螺纹看作在d1(内径)处展开的悬臂梁，此破坏截面的抗力函数:

式中:fw——螺纹牙的抗弯强度(kPa);

h——螺纹牙的工作高度，对于公制基本三角形螺纹标准h=0.655P。

1.2.7外锚头处螺纹危险截面拉断破坏模式螺栓危险截面提供的抗力函数:

式中:fs——锚杆螺丝端杆的杆体净截面承载力(kPa)。

2 双滑块岩质边坡锚固系统可靠性分析模型

2.1 双滑块边坡锚固系统安全系数计算

由于工程实际问题的复杂性，所以当锚杆发生破坏时将很难确定到底是哪种破坏模式起决定作用，但是发生破坏的肯定是提供抗力里最小的。

本文的边坡稳定性分析模型如图3所示。边坡体内含有一主控弱面CE。在边坡滑体上部主动滑块体沿弱面CE移动，下部的被动滑块体可能沿着潜在滑动面AD面剪出破坏。假定作用在锚固系统中的锚杆一共有n根，由于潜在滑动面AD面的存在，使得作用在主动滑块上的锚杆有m根，作用在被动滑块上的锚杆有n－m根。根据刚体极限平衡法，考虑锚杆多失效模式，推导被动滑块锚固系统的安全系数，公式如下:

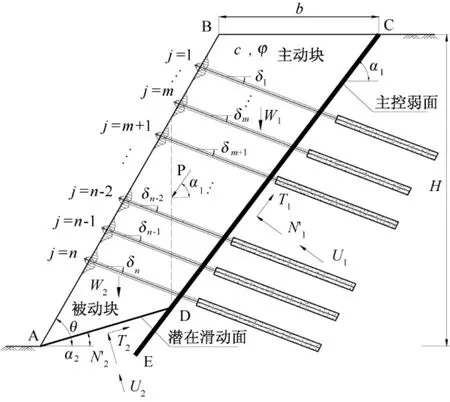
图3 双滑块边坡锚固模型Fig.3 The slope with multiple sliding-planes

其中:Fs——边坡安全系数，极限状态取1;

W1和W2——分别为上部主动滑块和下部被动滑块的自重(kN);

α1和α2——分别为主控软弱面和被动滑块潜在滑裂面的倾角(°);

Rj，min——第j根锚杆的最小抗力值(kN);

δj——第j根锚杆与水平面的夹角(°)，仰角为负，俯角为正;

U2——作用在被动滑块滑动面上的静水压力(kN);

φ1和φ2——主控软弱面上和被动滑块滑裂面上的内摩角(°);

c1、c2——分别为主控软弱面上和被动滑块滑裂面上的粘聚力(kPa);

L1、L2——主控软弱面和被动滑块滑裂面长度;

s——锚杆的水平间距;

H——滑体的高度;

θ——边坡的平均坡角(°);

b——坡顶面上主控弱面出露处到眉线的距离;

P——上部主动滑块的剩余下滑力，如果P＞0，两滑块间有相互作用力，否则，两滑块间就没有相互作用力;

图中:N′1、N′2——主控弱面和被动滑块滑裂面上的有效正应力(kN);

τ1、τ2——主控弱面和被动滑块滑裂面上的剪应力(kPa)。

2.2 功能函数的建立

根据式(13)，可得功能函数表达式如下:

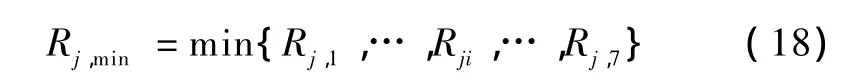
式中:G——功能函数;

R、S——分别为锚固系统的抗力、荷载;

U1——主控软弱滑动面上水的上托力;

Rji——第j排锚杆的第i种破坏模式截面所提供的抗力值。

3 锚固系统破坏概率计算流程

本文采用MATLAB语言编制程序完成蒙特卡罗(Monte carlo)随机抽样法分析考虑锚杆多种失效模式的岩质边坡双滑块锚固系统的可靠性，其具体步骤如下:

(1)首先为每一个随机变量定一个统一的随机抽样空间维数n，利用MATLAB软件的内置函数产生在开区间(0，1)上的均匀分布随机数，然后在此基础上，用坐标变换法变换成给定分布变量的各参数随机数，一共n组;

(2)在进行第i次抽样时，将第1步求出的第i组随机数代入(18)式，求选出每根锚杆的最小抗力函数值;同时也要判断(14)式是否大于0，如果大于0，把所求值代入(16)、(17)式计算;否则令(16)、(17)中的P值为0;

(3)将第(2)步抽样算出的(16)、(17)式的值代入功能函数(15)式，判断其与0的大小关系，来统计功能函数小于0的累积破坏次数;

(4)在进行n次抽样时，重复第(2)、(3)步，统计出锚固系统累积破坏次数为jn，根据结构失效概率公式Pf=jn/n，求得锚固系统的破坏概率。

4 算例与讨论

4.1 算例边坡未加固稳定性分析

一个高30m的风化石英岩边坡，坡面倾角60°;岩体的容重为rG=25kN/m3;边坡体内的主控弱面为夹泥层，弱面倾角为α1=55°，在坡顶面上出露点距边坡眉线12m。各随机变量概率统计参数见表1。

未加固的岩质边坡，以安全系数为目标函数，在主动滑块倾角α1、滑体高度H和主控弱面的位置b不变的情况下，搜索被动滑块的最危险的滑裂面倾角。经计算得知，随着α2的增大，边坡安全系数先减小后增大，中间存在极小值，α2=30°为最危险裂面倾角，其安全系数FSmin=1.03，如图4所示，虽然安全系数大于1，但不满足工程设计要求。

表1 随机变量参数Table 1 Random variable parameters

图4 未加固边坡在不同α2的边坡安全系数Fig.4 Factors of safety of unreinforced slope with different α2

基于蒙特卡洛法，求不同α2的未加固边坡的破坏概率，来搜索被动滑块的最危险倾角，如图5所示。由图可知，随着α2的增大，其破坏概率先增大后减小，在29°出现极大值，破坏概率达41.89%，在边坡可靠性分析中，属于危险性中等，说明该边坡具有较高的破坏概率。

4.2 算例边坡的锚固方案

本边坡为Ⅱ级边坡工程，若使其安全系数要达1.3［12］，则经计算所需的锚固力为620.5kN/m。设计锚杆参数见表2。本文为了提高锚头螺纹各种破坏截面的可靠性，螺丝端杆的直径要大于锚杆自由段和锚固段的钢筋直径，且螺丝端杆与自由段采用绑焊的方式连接。

4.3 锚固角对锚固边坡稳定性的影响分析

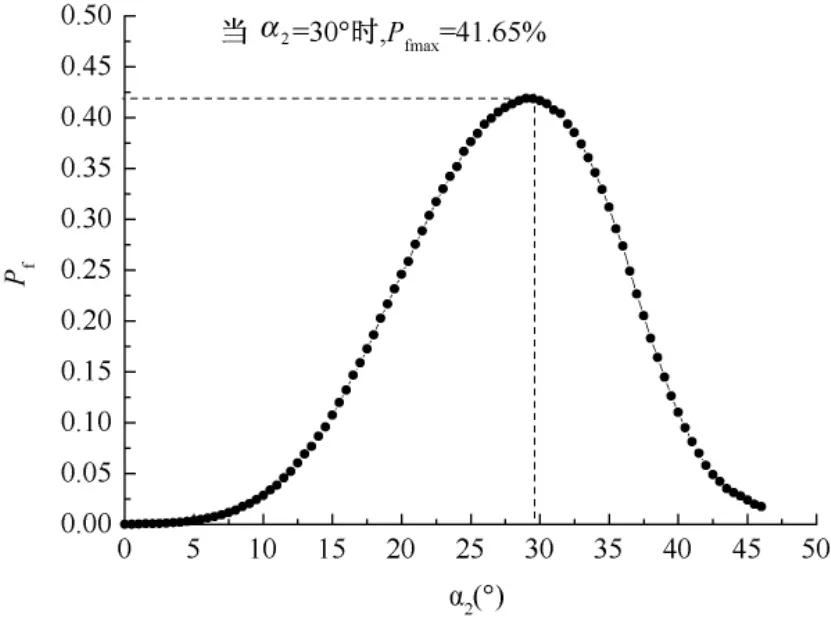
图5 未加固边坡在不同α2的破坏概率Fig.5 Failure probability of unreinforced slope with different α2

基于中值安全系数法来寻求锚杆的最优锚固角，如图6所示。随着锚固角的增大，锚固系统的安全系数先增大后减小，在δ=－14°附近出现最优锚固角的情况，最大安全系数达1.395。

如果考虑本文所提到的各随机参数的不确定性，以锚固系统的破坏概率为目标函数来锚杆的锚固角对边坡稳定性的影响，经计算，其锚固系统的破坏概率随着锚固角(俯角为正，仰角为负)的增加而先减小后增加，如图7所示。从图中可看出，在δ=－3°时出现最优锚固角，对应最小破坏概率达5.58%。

表2 锚杆设计参数表Table 2 Parameters of bolts

按目前常用锚杆(锚索)方向角的计算公式［14，15］，以主控软弱滑动面上强度参数为依据，求锚杆最佳倾角为δ=45°+15°/2－55°=－2.5°。而基于中值安全系数得出的最优锚固角为－14°，与经验公式所求结果相差－11.5°。而根据本文考虑把锚杆多失效模式考虑到锚固系统可靠性分析模型中，基于蒙特卡罗随机抽样，将岩质边坡锚固系统的破坏概率作为目标函数来寻求锚杆的最优锚固角为－3°，这与经验公式的计算结果基本一致。

图6 不同锚固角下的安全系数Fig.6 Factors of safety of different anchorage angles

图7 不同锚固角下的破坏概率Fig.7 Failure probability of different anchorage angles

4.4 被动滑块滑裂面倾角对锚固系统稳定性影响

为了注浆方便和灌浆质量，且满足稳定性的要求，先取锚杆锚固角为15°，这时锚固系统的破坏概率达6.79%＜10%，属于可以接受的破坏概率。在锚固系统中，当主控软弱面位置不变，坡高不变的情况下，且不考虑滑动面强度参数因锚杆的锚固作用而发生变化时，基于中值安全系数法，分析被动滑块滑裂面倾角α2对双滑块岩质边坡稳定性的影响，如图8所示。锚固系统的安全系数随着α2的增大而先减小后增大，在α2=27°得到安全系数FS的极小值点，达1.31＞1.3，满足Ⅱ级边坡工程设计要求，这与加固前搜索到被动滑块的最危险滑裂面的倾角30°相差不大。

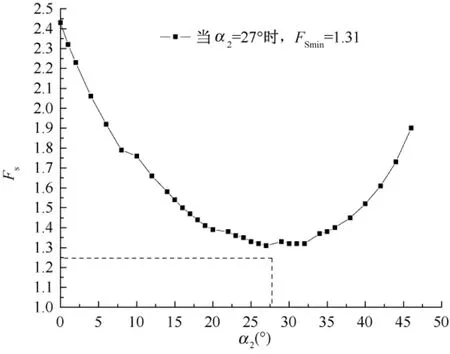
图8 锚固系统中不同α2下的安全系数曲线Fig.8 Factors of safety of differentα2in the of the anchorange system

如果在与上面同样的条件下，把锚杆的多种失效模式考虑到锚固系统可靠性分析模型中，基于蒙特卡罗随机抽样法，考虑各参数的不确定性来分析被动滑块滑裂面倾角与锚固系统稳定的影响，如图9所示。锚固系统的破坏概率随着被动滑块的滑裂面倾角的增大而先增大后减小，且在α2=28°处出现极大值点，最大破坏概率达5.597%＜10%。通过图8、图9的比较，在不考虑滑动面上抗剪强度受锚杆锚固作用的影响，通过中值安全系数法与考虑锚杆多失效模式情况下的蒙特卡罗法两种方法求出的被动滑块最危险滑裂面的位置基本一致。

图9 不同α2下的破坏概率曲线Fig.9 Failure probability of different α2

通过图4与图8的比较、图5与图9的比较可知，中值安全系数法和蒙特卡罗法两种方法所算曲线都得出了一致的规律:在不考虑锚杆锚固作用对滑裂面强度参数影响的情况下，被动滑块滑裂面倾角对双滑块模型的岩质边坡加固前后的稳定性影响规律一致。

通过图6与图8的比较、图7与图9的比较可知，锚杆的锚固角对锚固系统的影响规律与被动块滑裂面对锚固系统的影响规律相反。

5 结语

本文利用蒙特卡罗随机抽样法，分析了考虑锚杆多失效模式的岩质边坡双滑块锚固系统稳定性模型，得出了以下几个结论:

(1)在不考虑主控软弱面强度参数受锚杆锚固作用影响的情况下，岩质边坡锚固前后的α2－FS曲线的变化规律基本一致;

(2)在不考虑锚杆的锚固作用对软弱滑动面强度参数c、φ影响，且主控软弱面位置不变、坡高不变的情况下，被动滑块的滑裂面倾角对未加固边坡和锚固边坡的稳定性影响规律一致，边坡破坏概率随着被动滑块倾角α2的增大而先增大后减小，安全系数随着α2增大而先减小后增大;

(3)考虑锚杆多失效破坏模式和岩土体参数的不确定性的边坡锚固系统可靠性计算结果比中值安全系数法的计算结果更能真实、合理地反映出各参数给岩质锚固系统可靠性带来的影响;

(4)锚杆锚固角对锚固系统稳定性的影响规律与被动滑块滑裂面倾角对锚固系统稳定性的影响规律相反。

［1］DUZGUNH S B，YACEMEN M S，KORPUZ C A.A methodology for reliability－based design of rock slopes ［J］.Rock Mechanics and Rock Engineering，2003，36 (2):95－120.

［2］陈昌富，王贻荪，邹银生.边坡可靠性分析分步混合遗传算法［J］.土木工程学报，2003，36(2):72－76.

［3］张兴，廖国华.多滑动面边坡的破坏概率［J］.岩土工程学报，1990，12(6):55－62.

［4］吴震宇，陈建康，许唯临，等.岩质边坡稳定的体系可靠度分析及工程应用［J］.四川大学学报(工程科学版)，2008，40(2):32－37.

［5］李典庆，周创兵.考虑多失效模式相关的岩质边坡体系可靠度分析［J］.岩石力学与工程学报，2009，28 (3):541－551.

［6］陈昌富，彭振斌.含主控弱面双滑块破坏边坡可靠度优化分析［J］.中南工业大学学报，1996，27(4):387－391.

［7］张发明，刘宁，赵维炳，等.岩质边坡预应力锚索加固的优化设计方法［J］.岩土力学，2002，23(2):187－190.

［8］熊文林，何则干，陈胜宏，等.边坡加固中预应力锚索方向角的优化设计［J］.岩石力学与工程学报，2005，24(13):2260－2265.

［9］闫莫明，徐祯祥，苏自约.岩土锚固技术手册［M］.北京:人民交通出版社，2004.

［10］许镇宇，朱景梓，郑林庆，等.机械零件［M］.北京:人民交通出版社，1960:151－155.

［11］钱家欢，殷宗泽.土工原理与计算［M］.北京:中国水利水电出版社，1980:345－360.

［12］GB 50330－2002.建筑边坡工程技术规范［S］.

［13］张建国，苏多，刘英卫.机械产品可靠性分析与优化［M］.北京:电子工业出版社，2008.

［14］赵长海，董在志，陈群香.预应力锚固技术［M］.北京:中国水利水电出版社，2001:19－25.

［15］陈胜宏，陈敏林，赖国伟.水工建筑物［M］.北京:中国水利水电出版社，2004.

Abstract:The system reliability assessment model for the anchorange system of rock slope with many rock bolts was established，based on system reliability theory and limit equilibrium method，considering many possible failure modes of the anchor itself，such as the tensile failure of the free section，the shear failure between pull rod and grouting mass，grouting mass pulled out from surrounding rock and the failure of the rock below the mat piers，etc.A direct calculated method was presented to perform the probability of failure of the anchorange system for this kind of slopes，by making use of the random sampling idea of Monte Carlo technique.Lastly，with the examples for calculations，the paper analyzed the effects of the calculation parameters on the results，and discussed the effects of the anchorage angle of anchor and the inclination of passive slider on the stability of the anchorange system，based on the median factor of safety and the failure probability index.

Key words:slope engineering;rock slope;anchorage system;failure probability;system reliability;optimal anchorage angle

Reliability analysis of anchorage system considering mulitiple failure modes of bolts of bi-block slide

CHEN Chang－fu，CHENG Xiao－wei
(Geotechnical Engineering Institute of Hunan University，Changsha410082，China)

1003－8035(2010)03－0001－07

TD824.7

A

2010－05－07;

2010－06－12

国家自然科学基金(50878082);湖南省自然科学基金(09JJ3104);交通西部项目(200631880237)

陈昌富(1963—)，男，湖南祁东人，教授，博士生导师，主要从事边坡与支挡结构、地基处理等研究。

E－mail:ccf－students@163.com