双层海底管道跨越设计的垂向屈曲研究＊

赵天奉段梦兰潘晓东冯现洪

(1.中国石油大学(北京)机械与储运工程学院海洋油气研究中心; 2.海洋石油工程股份有限公司)

双层海底管道跨越设计的垂向屈曲研究＊

赵天奉1段梦兰1潘晓东2冯现洪2

(1.中国石油大学(北京)机械与储运工程学院海洋油气研究中心; 2.海洋石油工程股份有限公司)

以惠州A海底管道为例,提出了双层海底管道垂向屈曲分析的新方法,并研究了高温双层海底管道跨越段的垂向屈曲特性。应用改进的Riks算法计算非单调载荷与位移的响应历程,得到的管道变形和应力状态可以充分描述高温载荷下双层管道跨越段的垂向屈曲过程。双层海底管道的跨越设计既需要考虑跨越构形引发的应力应变,也需要充分校核管道跨越段的垂向稳定性。关键词 双层海底管道 跨越设计 垂向屈曲 Riks算法

双层海底管道是海洋油气高温输送的常用结构,但是评估校核其热稳定性的分析技术目前仍不够完善,现有的规范均没有提供双层海底管道屈曲分析的直接方法。事实上,无论是单层海底管道还是双层海底管道,也无论是埋设海底管道还是非埋设海底管道,在承担热载荷后管道内轴向力的增加均有可能引发管体屈曲(即管道离开初始直线位置发生大挠度的几何变形),该过程类似于梁在轴向载荷达到临界值时发生的欧拉屈曲。海底管道屈曲被分为垂向屈曲和侧向屈曲,针对双层海底管道,各船级社规范均明确提出了对这两种屈曲的校核要求。

尽管海底管道热屈曲问题迄今尚未得到充分解决,但许多学者在这个领域已做过大量工作并取得一定成果,这些成果在海底管道工程设计中发挥了重要的指导作用。1984年R.F.Hobbs发表了首篇评价海底管道屈曲的论文,推导出了单层管道垂向屈曲及侧向屈曲的解析公式,并用于计算管道的屈曲波长、屈曲轴向力和屈曲位移幅值[1]。R.F. Hobbs和F.Liang应用文献[1]方法解决了半无限长管道的热屈曲问题[2]。N.Taylor与A.B.Gan进一步研究了管道铺设不直度对其屈曲特性的影响[3]。A.Bokaian研究了双层保温管道的热膨胀现象,对双层管道的热应力应变进行了计算[4]。Boreas Consultants,TWI和Cambridge大学2002年发起的“SAFEBUCK”或“The Safe Design of Hot on-Bottom Pipelines with Lateral Buckling”[5]项目的研究成果认为,管道屈曲的发生主要由3个参量控制:管道轴力、管道不直度与管道侧向约束。尽管只有3个控制参量,但每个参量却涉及很多实际的变量,这使其真实大小存在很大的不确定性。1999年M.A.Vaz与M.H.Patel提出了计算双层保温管道屈曲失稳的解析公式[6],对双层保温管道的挠曲线方程、平衡外力、侧向位移耦合方程进行了联立求解,并对管道垫块的等间距分布及不等间距分布情况进行了讨论。M.A.Vaz与M.H.Patel求耦合方程组的特征值解为双层海底管道热稳定性研究开辟了途径,但是他们的方程组中没有包含与屈曲的发生密切相关的管道初始不直度参数,致使其研究成果难以得到实际的应用。

本文以我国南海惠州A双层海底管道跨越设计的屈曲校核为例,提出了双层海底管道跨越段垂向屈曲的分析方法,研究了高温条件下双层海底管道跨越段的屈曲特性,研究结果可为双层海底管道的跨越设计提供支持。

1 改进的Riks算法

解决不稳定平衡问题的方法已经推出了若干种,其中最为成功的是改进的 Riks算法[7-8]。在研究不稳定平衡问题的载荷-位移响应曲线中,载荷与位移的单调关系在响应的历程中可能会发生变化,改进的Riks算法是求解这类问题有效解的算法。在Riks算法中,加载过程被假设为按比例实施的,即所有载荷的大小同时随某个标量参数变化,同时假设这个响应是光滑的,不会发生突然的分叉。该方法的本质在于,将失稳过程的解看作是节点变量和加载参数所定义空间中的一个平衡路径,而采用的最基本的算法仍然是牛顿法,因此在计算过程中将有一个有限的收敛半径。

在改进的Riks算法中,载荷-位移空间中平衡路径增量的大小即为沿切线方向到当前求解点所移动的距离,而该距离的大小是由与收敛速度相关的自动增量算法所决定的。在计算过程中,需要在通过求解点并且垂直于切线的平面内寻找载荷-位移空间中的平衡点。

设 PN为载荷模式(N=1,2,…,有限元模型总自由度数目),由一个或多个载荷项所定义,设λ为载荷大小的标量参数;所以在任何时候实际载荷为λPN;设 uN为此时的位移。

2 惠州A双层海底管道跨越段结构特点

惠州A海底管道为典型的双层保温管道,图1为其结构简图。

图1 惠州A双层海底管道结构简图(mm)

为跨越某海底电缆,特别在惠州A管道与电缆交叉点附近设计了4组支撑沉垫将管道撑起,其结构示意于图2。该管段的跨越长度为116m,支撑沉垫组的约束分为两种:在跨越位置外侧的2个沉垫组应用Ⅰ型约束,底部沉垫组高度为30cm,其上部铺设管道并用覆盖沉垫组压住(图3);在跨越位置中部的2个沉垫组应用Ⅱ型约束,底部沉垫组高度为50cm(图4)。

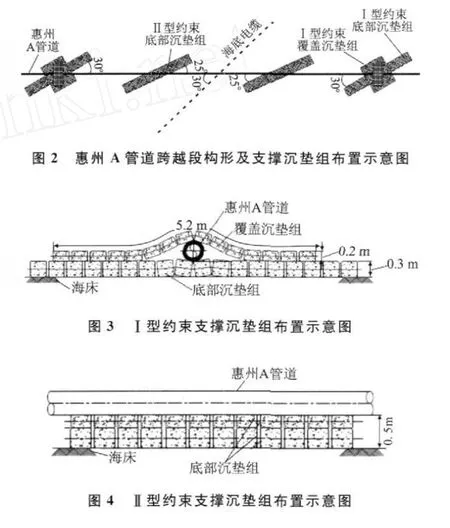
跨越段的存在,相当于双层管道在跨越位置上具有了促使垂向屈曲发生的初始不直度,因此该位置处管道的临界屈曲载荷会下降;若这个临界值接近跨越段将要承担的实际热载荷,跨越段就有可能发生垂向屈曲。垂向屈曲发生后管道的轴向力、自重和沉垫组的支撑力将在垂向上建立起平衡。当跨越段管道离开中部沉垫组时,在侧向上将失去摩擦力的约束,此时屈曲构形有可能跃迁到侧向模态上去,致使跨越段管道随即发生倾倒。

3 惠州A管道跨越段垂向屈曲分析

惠州A管道输送介质的输入温度为115℃,取海底年平均温度18.1℃为安装温度,不妨以96.9℃(即115℃～18.1℃)定义载荷比例因子(LPF)。分析中LPF值为1.0时该增量步上加载的热载荷为96.9℃。

首先用AutoPipe软件分析铺设到沉垫组位置后双层管道的变形状态,以获得管道在跨越位置的铺设构形,然后根据该构形形态建立管道屈曲分析的有限元模型,即直接以有限元网格对双层管道跨越段的初始不直度进行模拟,以S4R壳单元模拟内外管层,以C3D8R体单元模拟环形空间中的木制垫块,定义内外管层与垫块之间的接触关系。分析中,在Ⅰ型沉垫组位置采用完全锚固边界条件,在Ⅱ型沉垫组位置可用非线性弹簧单元施加的弹簧力模拟支撑力,当管道发生垂向屈曲离开沉垫组时,相关的弹簧力定义为零。

这项分析需分两步进行,第一步为静力分析,建立起管道浮力、重力与沉垫支撑力之间的平衡,第二步为热载荷作用下的管道屈曲分析。当热载荷引发的轴向力达到管道跨越段或其局部管段的屈曲临界值时,跨越段的整体或局部将发生垂向屈曲,离开Ⅱ型沉垫组的支撑平面。

图5为分析得到的惠州A管道跨越段垂向屈曲弧长与载荷比例因子关系曲线,图中对几个关键的增量步进行了标注:A点意味着双层管道的内管在环形空间发生了屈曲;B点意味着管道跨越段整体发生了垂向屈曲;C增量步对应着跨越段的后屈曲模态跃迁。A、B、C等3个分析增量步对应的内外管构形见图6(垂向变形放大100倍显示;由于环形空间中木制垫块在一定程度上会受压变形,因此内外管的弯曲形态并不完全一致)。

图5所示弧长与载荷比例因子关系曲线中载荷比例因子的最大值为0.838 670,这表明惠州A管道在跨越位置保持垂向稳定的热承载能力是有限的。结合各增量步下管道的变形状态,可认为图5中B点对应的载荷比例因子值0.820 106为管道跨越段的垂向屈曲临界载荷值;该比例因子值对应的实际加载温度为79.5℃,若安装温度为18.1℃,那么跨越段发生垂向屈曲的临界温度就为97.6℃。尽管惠州A管道的设计入口温度达到115℃,但据沿程温降曲线管道跨越位置处的预期输送温度则为96℃(跨越位置靠近管道登陆终端),由此可初步地认为该管道现有跨越设计可满足热载荷作用下的垂向稳定要求,但可承载余量较小。

分析中假设Ⅰ型支撑完全约束了跨越段两端的垂向运动,但实际上Ⅰ型支撑覆盖沉垫组的垂向约束力是有限的,需要加以校核。因为,若覆盖沉垫组的垂向约束力不足,则覆盖沉垫组可能在管道垂向屈曲过程中被顶起,引发管道跨越段侧向屈曲,带来危险的后果。图7给出了跨越段垂向屈曲过程中Ⅰ型支撑沉垫组的垂向约束反力曲线(跨越段左、右两侧支撑沉垫组的垂向约束反力分别以绿色和红色两条曲线表示),该曲线仍以分析弧长为自变量,并对应地标注出了图5中的5个增量步,其中A、E两点的垂向约束反力为负值,意味着此时管道在Ⅰ型支撑位置向上顶覆盖沉垫组;B、C、D等3点的垂向约束反力为正值,意味着此时管道在Ⅰ型支撑位置向下压底部沉垫组。由图7可见,在A点管道所需要的覆盖沉垫组垂向约束力最大(5.59kN),因此该值可用于校核覆盖沉垫组的垂向约束力。

图5 惠州A管道跨越段屈曲弧长与载荷比例因子关系曲线

图6 惠州A管道跨越段屈曲的3个构形

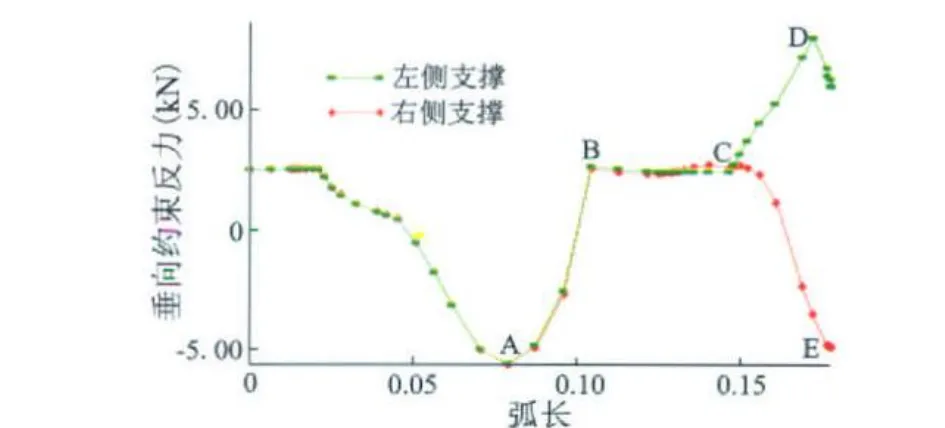
图7 惠州A管道屈曲过程中Ⅰ型支撑位置处的垂向约束反力曲线

在Ⅰ型支撑位置处,管道的最大上顶力并没有出现在管道屈曲发生的时刻(B点),而是出现在屈曲发生之前的A点。从B点到C点,管道的垂向屈曲模态发生了从一阶到二阶的跃迁,两侧曲线的构形不再对称,导致左右两侧Ⅰ型支撑的垂向约束反力作用方向发生了变化;此时在左侧管道对Ⅰ型支撑的底部沉垫组向下压,在右侧管道对Ⅰ型支撑的覆盖沉垫组向上顶。图8给出了左右两侧Ⅰ型支撑的垂向约束反力矩曲线,表1列出了5个典型增量步的分析结果。

表1所列结果表明,加载到C增量步时,垂向屈曲的管道跨越段发生了模态跃迁,在管道内尤其是外管内引发了显著的应力集中,而此时跨越段的热承载能力并没有显著提升,这意味着跨越段发生垂向屈曲后随时可能发生屈曲模态跃迁,因此屈曲模态跃迁是双层海底管道跨越设计除覆盖沉垫组约束力不足外的另一个潜在隐患,需要在设计校核阶段加以注意。

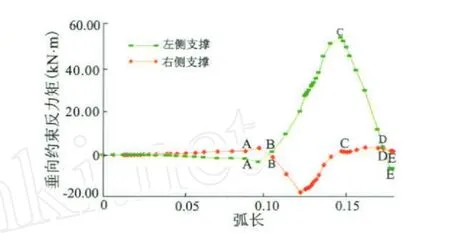
图8 惠州A管道屈曲过程中Ⅰ型支撑位置处的垂向约束反力矩曲线

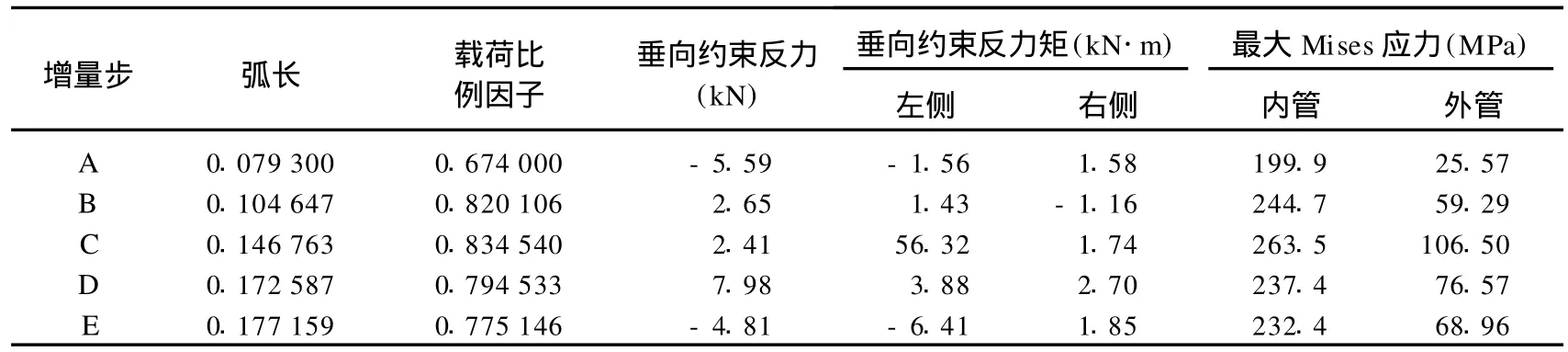
表1 惠州A管道屈曲分析中典型增量步的分析结果

4 结论

(1)本文所提供的有限元分析方法能够模拟双层海底管道跨越段的垂向屈曲过程,并能校核管道跨越设计中覆盖沉垫组提供的垂向约束力是否满足需求,可为双层海底管道的跨越设计提供支持。

(2)本文有限元模型是直接依据管道跨越段的铺设构形构建的,在分析中忽略了管道内的铺设预拉应力。鉴于拉应力会在一定程度上缓解温度载荷引起的管道轴向力,对铺设预拉应力的忽略使得分析结果比较保守,故可对分析结果进行修正,将分析得到的管道临界屈曲温度增加若干度,以平衡管道内部的初始拉应力。

(3)在高温双层海底管道跨越段的设计中,既要考虑跨越构形引起的铺设应力变化,也要校核跨越构形下管道的垂向稳定性。

本项研究分别得到海洋石油工程股份有限公司和中海油研究总院的资助,挪威船级社和美国船级社对中国石油大学(北京)承担的相关项目进行了第三方审核,在此表示衷心感谢。

[1] HOBBS R E.In-service buckling of heated pipelines[J].Journal of Transportation Engineering,1984,110(2):175-189.

[2] HOBBS R E,LIANG F.Thermal buckling of pipelines closed to restraints[C].International Conference on Offshore Mechanics and Arctic Engineering,1989,5:121-127.

[3] TAYLOR N,GAN A B.Submarine pipeline buckling-imperfection studies[J].Thin Walled Structures,1986,4:295-323.

[4] BOKAIAN A.Thermal expansion of pipe-in-pipe systems[J]. Marine Structure,2004,17:475-500.

[5] BRUTON D,CARR M,CRAWFORD M,et al.The safe design of hot on-bottom pipelines with lateral buckling using the design guideline developed by the SAFEBUCKjoint industry project,Deep Offshore Technology Conference[C].Espirito Santo,Brazil.2005.

[6] VAZ M A,PATEL M H.Lateral buckling of bundled pipe systems[J].Marine Structure,1999,12:21-40.

[7] RIKS E.An incremental approach to the solution of snappingand buckling problems[J].Int.J.Solids and Structures,1979, 15:529-551.

[8] ZHAO T F,DUAN M L,PAN X D.Lateral buckling performances of untrenched HT PIP systems,proceedings of International Conference on Offshore and Polar Engineering[C].Lisbon,July1-6,2007,2:945-950.

(编辑:张金棣)

Abstract:For the submarine pipeline A of Huizhou oilfield,a new method has been presented for analyzing the upheaval buckling of submarine pipe-inpipe system and the research has been carried out on the upheaval buckling characteristics of crossing section of high temperature submarine PIP system. In this method,the modified Riks algorithm is used to calculate the non-monotonic load and displacement response histories and the resulted pipeline deformation and stress can present a full description on the upheaval buckling process of the crossing section of high temperature pipe-in-pipe system.For the crossing section design of the pipe-in-pipe systems,it is necessary to consider the stress-strain initiated by crossing configuration and check the vertical stability of the crossing section.

Key words:pipe-in-pipe systems;the crossing section design;upheaval buckling;Riks algorithm

Upheaval buckling in the crossing section of submarine pipe-in-pipe systems

Zhao Tianfeng1Duan Menglan1
Pan Xiaodong2Feng Xianhong2
(1.Of f shore Oil&Gas Research Center,School of Mechanical and Transportation Engineering, China University ofPetroleum,Beijing,102249;
2.Of f shore Oil Engineering Co.,Ltd., CNOOC,Tianjin,300452)

2009-09-07 改回日期:2009-11-26

＊国家自然科学基金资助重点项目“深水双层海底管道热屈曲特性及控制”(50979113)部分研究成果。

赵天奉,男,讲师,2008年毕业于大连理工大学,获博士学位,主要从事海洋工程结构研究。地址:北京市昌平区府学路18号(邮编:102249)。E-mail:zhaotianfeng@sina.com。