基于RFM的高分辨率卫星遥感影像自动匹配研究
季顺平,袁修孝
武汉大学遥感信息工程学院,湖北武汉430079
基于RFM的高分辨率卫星遥感影像自动匹配研究
季顺平,袁修孝
武汉大学遥感信息工程学院,湖北武汉430079
提出一种基于有理多项式模型(RFM)的高分辨率卫星遥感影像自动匹配方法。首先利用RFM进行高分辨率卫星影像直接定位和同名点预测,并分析预测精度;然后基于投影轨迹建立近似核线方程,并分析核线精度;接着采用金字塔影像策略进行核线约束的近似一维影像匹配,并经最小二乘影像匹配精化匹配结果;最后采用RANSAC算法剔除误匹配点以获取最终的匹配结果。试验结果表明,该方法的匹配成功率和稳定性高于传统的二维灰度匹配方法和现流行的SIFT匹配方法,能够很好地解决高分辨率卫星遥感影像自动匹配中不同成像模式、多时相、大姿态角等情况导致的匹配难题。
影像匹配;核线方程;RANSAC;RFM
1 引 言
由于高分辨率卫星遥感影像物理成像模型的复杂性及多视角、多时相的问题,其立体像对的自动匹配一直是一个研究热点和难点。近年来,该项研究已取得一定的进展。文献[1]研究基于SIFT特征的遥感影像自动配准,指出该方法在图像具有较复杂变形的情况下,仍然可以准确匹配到大量的稳定特征,但该试验只采用较小的影像局部区域,因此应用于大容量遥感影像的可行性和效率仍需进一步研究。文献[2]设计一种新的全局一致性度量准则,实现了基于空间关系的遥感影像特征匹配,通过与几种经典度量准则的比较分析,证实该方法的正确性和稳健性,但仍克服不了基于空间关系的匹配方法一些固有的缺陷。文献[3]针对多源遥感影像人工几何纠正方法存在精度差、效率低等问题,提出一套基于匹配技术的自动纠正算法流程。首先通过手工选择控制点进行仿射变换实现粗配准,并采用小波影像金字塔的逐级匹配策略获得控制点对,再利用多项式拟合剔除错误点对,最后采用不规则三角网实现影像纠正。文献[4]基于文献[3]进行进一步研究,采用SIFT算法匹配出少量同名点用于粗配准,而无须再手工选择控制点。文献[5-6]采用几何约束的相关算法实现基于多基线影像匹配的高分辨率遥感影像的DEM生成,自动匹配生成的DEM保持较好的精度和可靠性,但该方法需以影像的精确外方位元素作为初始条件。Kornus等采用一种改进的区域增长算法[7]生成同轨SPOT5三立体像对(前视、后视、正视)的DEM[8],该方法也需要在匹配前手工选择一定数量的种子点。
综上所述,虽然高分辨率卫星遥感影像的匹配研究已经取得一定的进展,但大部分算法仍需手工给定初始条件或种子点,目前仍没有一种成熟的算法能够稳健可靠地实现各种条件下高分辨率卫星遥感影像的全自动匹配;同样,无论是在数字摄影测量工作站(如VirtuoZo、J X4)上进行立体模型定向,还是采用遥感应用软件(如 ERDAS、PCI)进行影像配准,亦首先要手工选定一定数量的控制点。
为解决高分辨率卫星遥感影像匹配仍需人工干预的难题,减少多时相、大倾角立体像对对匹配结果的影响,本文研究一种基于RFM模型的影像匹配方法,以提高自动匹配的可靠性和成功率,为后继的模型定向、影像配准、DEM生成等作业提供可靠的、高精度的同名特征点。
2 基于RFM的近似核线匹配原理
本文匹配方法的主要流程如图1所示,首先采用RFM模型预测初始同名点,然后根据投影轨迹法生成近似核线约束同名点搜索范围,再进行金字塔影像匹配和最小二乘匹配,并采用RANSAC算法剔除误匹配点,实现高分辨率卫星遥感影像的自动匹配。

图1 基于RFM的近似核线匹配流程图Fig.1 Flow chart of approximate epipolar matching method based on RFM
2.1 基于RFM的同名点预测
目前几种常用的高分辨率卫星遥感影像中,例如QuickBird、IKONOS等,都提供基于有理多项式的传感器成像模型(RFM),SPOT 5提供的严格几何模型也可非常方便地转换为RFM模型。RFM对严格物理成像模型的拟合精度很高,一般在0.01像素数量级[9-11]。因此,采用RFM进行对地定位和采用严格物理模型进行定位的精度几乎完全一致。
RFM的反解公式(从地面到影像)为

其中,P、L、H为正则化地面坐标;X、Y为正则化影像坐标;N umS、N umL为多项式分子;DenS、DenL为多项式分母。具体含义详见文献[12]。由于厂商提供的RPC参数文件中只提供反解公式的系数,为进行正变换,需对式(1)进行线性化

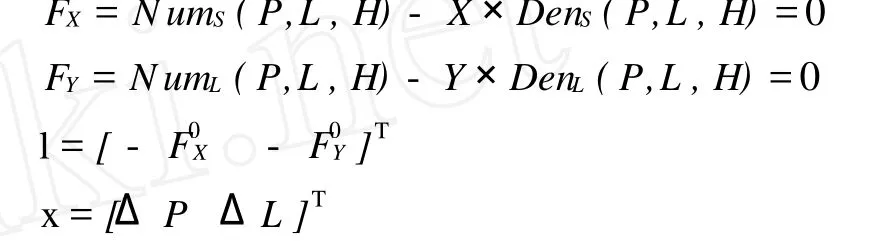
根据最小二乘原理,给定合适的 P、L初值,可求出地面点坐标

采用特征提取算子在基准影像上提取特征点后,根据式(3)可将特征点的影像坐标投影至地面,再由式(1)反投到待匹配影像上,获得同名点匹配初值。为确定搜索范围和建立恰当的金字塔层数,需分析同名点的预测精度。
若已知地面高程,则匹配初值的精度仅由RPC参数的精度决定。笔者利用立体像对上的检查点对2组SPOT立体像对、1组QuickBird立体像对(见3.1)进行同名点位的预测精度分析。如表 1所示,x、y向的预测误差分别从1像素到40像素不等,其中两组SPOT异轨立体像对预测精度明显高于QuickBird同轨立体像对的预测精度,且与Reinartz等的SPOT直接定位结果较为一致[13]。总而言之,3组立体像对的预测误差都在40像素之内,这表明厂商提供的RPC参数具有一定的精度,同时为金字塔层数的确定提供了参考依据。

表1 基于RFM的同名点预测精度Tab.1 The accuracy of correspondence point prediction based on RFM
由于卫星高度达到几百公里,地面高程误差影响不大。当高程分别变化1 m、10 m、100 m、500 m时,该预测点位与初始预测点位的平均误差如表2所示。从表2中看出,对于SPOT异轨立体像对而言,高程的变化主要影响 x方向的误差,对 y方向即核线方向影响较小。当高差达到500 m时,x方向的预测误差在100像素之内,对y方向几乎没有影响。对于同轨立体模式,预测误差则大得多,当高差达到500 m时,x方向的预测误差为166像素, y方向的预测误差则接近700像素。因此,对于同轨立体像对而言,需要将扫描线旋转90°后再建立近似核线,统计核线方向预测误差。

表2 高程变化对预测位置的影响Tab.2 The prediction error due to height change
2.2 基于投影轨迹的近似核线
在推扫式卫星遥感影像中,每一扫描行均有其自身的投影中心和方位元素,因此它并不存在严格的核线定义。常用的近似核线理论包括多项式拟合法[14]和基于光点升降的投影轨迹法[15]。多项式拟合法需要相当数量的已知同名点,该条件在影像匹配前是无法满足的。而投影轨迹法则需要影像的外方位元素,因此在RPC参数已知并且精度较高的情况下,采用投影系数法生成近似核线作为匹配约束条件。
如图2所示,当地面高程为 H时,由式(3)计算出左像上任一点p在地面的坐标为Q,由式(1)计算出右像的坐标为q(x,y);当地面高程为 H′时,p在右像的反投影坐标为q′(x′,y′)。则 p点在右像上的核线是过q和q′的一条曲线。而在实际影像范围内,该曲线可近似为一直线[16]。其斜率可用式(4)计算


图2 基于投影轨迹的推扫式影像核线示意图Fig.2 Epipolar line of push-broom imagery based on projection track
2.3 金字塔影像的近似核线匹配策略
由于SPOT异轨立体像对的近似核线精度较高,实际匹配中金字塔层数的选择只由初始点位的预测误差决定。从表1和表2看出,y方向的预测误差一般在10像素以内,高程预测误差即使达到500 m也才引起 x方向最大88.5像素的误差。因此,若建立2层金字塔,y方向搜索范围设置为3像素,x方向设置为50像素,则实际在原始影像上的搜索范围分别是 27像素和450像素,完全可满足同名点搜索的需要。
而同轨立体像对由于侧视角的巨大差异,左右影像间变形严重,也导致核线存在较大的倾角。虽然推扫式影像不再满足中心投影关系,但在局部匹配窗口内,仍可近似为中心投影。因此,和航空影像类似,可采用核线采样来消除姿态角引起的影像变形,同时消除核线方向的预测误差。
令高程变化引起的预测同名点位到近似核线的偏差Δy为

其中,(x,y)为同名点预测坐标;k为核线斜率。
表3示意将QuickBird立体像对旋转90°后,高程变化时引起的预测点位到核线的预测偏差。由此可见,对搜索窗口重采样后,即使高差达到500 m,利用投影轨迹法获得的核线预测精度也高于3像素。

表3 高程变化引起的核线偏差Tab.3 Epipolar bias by height changes
综合考虑同轨和异轨立体像对RFM的预测误差和投影轨迹法的核线误差,在建立2层金字塔的情况下,若将核线方向搜索区间设置为3像素,x向搜索区间设为100像素,则原始影像上的搜索范围分别是27像素和900像素,可同时满足同轨和异轨立体像对匹配的需要。
在采用式(4)计算所有特征点的对应核线后,根据核线斜率决定是否进行局部匹配影像块重采样。为保证灰度相关算法的通用性和有效性,本文设定当k大于8°进行核线重采

其中,(X0,Y0)为匹配影像块中心坐标;(x,y)为原始影像坐标;(X,Y)为采样后影像坐标。
金字塔影像生成后,就可从顶层金字塔开始,逐层进行近似一维核线匹配,并传递到原始影像上进行最小二乘相关。
2.4 基于RANSAC算法的误匹配点剔除
在框幅式航空影像匹配中,一般采用核线约束或带模型连接条件的相对定向作为严格几何模型剔除误匹配点,保证匹配精度和可靠性。然而,高分辨率推扫式卫星影像每一扫描行各为中心投影,且外方位元素非精确已知,因而不存在严格的几何约束关系。因此,在高分辨率卫星影像的匹配或配准研究中,一般采用多项式拟合、透视变换等模拟公式作为几何约束模型,其中又以仿射变换应用最广[3-4,17]。卫星遥感影像飞行高度很高,若视地面水平,则透视变换模型可严格表达两幅影像间的投影关系,因此更为严格。本文采用透视变换方程作为误差模型,如下式所示

其中,(x,y)为基准影像上的特征点坐标;X、Y为待匹配片上的同名像点坐标;a1、a2、a3、b1、b2、b3、c1、c2为变换系数。
建立几何约束模型后,需选择粗差检测算法剔除误匹配点。传统的粗差探测算法包括Data Snooping、选权迭代法等,新兴算法则以随机采样一致性算法(RANSAC)为代表[18]。笔者通过大量试验,发现当大量粗差参与整体平差时,Data Snooping方法和选权迭代法都存在计算结果发散而剔除所有的同名点或只能剔除部分粗差的情形。而RANSAC算法采用随机抽样,从局部到整体的搜索策略进行粗差剔除,在高误匹配率情况下,表现更加稳定。因此本文采用RANSAC方法剔除误匹配点。
3 试验及其结果分析
3.1 试验设计
本文选用图3所示的三组高分辨率卫星遥感影像进行匹配试验。图3(a)、图3(b)为两组SPOT5异轨立体像对,像元地面分辨率约为5 m。其中图3(a)拍摄时间间隔一年,变化差异明显,为典型多时相影像,图3(b)拍摄时间间隔3 d。图3(c)为地面分辨率约1 m的 QuickBird同轨立体像对,拍摄时间间隔65 s,由于是同轨立体模式,俯仰角分别为-27.12°和26.46°,影像间存在较大的变形。三组立体像对大小皆为12 000像素×12 000像素。

图3 试验影像Fig.3 Test images
3.2 影像匹配结果
对于每一组立体像对,首先以3个像素为采样间隔,生成2层金字塔影像。采用Förstner算子提取特征点后,根据式(3)和式(1)预测初始同名点位,并根据式(4)计算核线斜率。然后进行近似核线的逐层金字塔影像相关,并在原始影像上进行最小二乘相关。顶层金字塔的搜索范围为 x方向100像素,y方向3像素。
为评价基于RFM和投影轨迹法的匹配方法的性能,这里同时采用传统的灰度相关算法和SIFT特征匹配算法[19]进行对比试验,两种方法皆采用C++语言编写,已集成到WuCAPS[20]自动量测程序中。其中,灰度相关算法采用先金字塔影像相关,再进行最小二乘影像匹配的方法,影像搜索区间设为15%像幅宽,金字塔影像设定为4层。SIFT特征匹配算法采用直接在原始影像上进行SIFT特征提取和匹配的方案,为提高匹配效率,采用瓦片分块的方法。三种方法的影像匹配结果一并列于表4。其中“匹配点”表示三种匹配方法未剔粗差前的匹配结果,“正确点”表示剔粗差后剩余的正确匹配点。

表4 三种匹配方法比较Tab.4 Comparison with three matching methods
3.3 结果分析
分析表4试验结果可以发现:
1.当采用传统灰度相关方法进行影像匹配时,三组立体像对平均正确匹配68对同名点。除了时差仅3天的SPOT异轨立体像对匹配166对同名点外,其他两组影像只匹配20对左右的同名点,正确匹配率是相当低的;采用SIFT匹配方法,三组立体像对的平均正确匹配92对同名点,略好于灰度相关算法,但匹配率仍然较低;而采用本文的方法,平均正确匹配197对同名点,三组立体像对的匹配成功率都得到明显提高。
从匹配残差来看,三种匹配方法的 y方向的中误差几乎都在0.5像素之下,精度很高;而x方向的中误差一般在1像素~1.5像素之间,虽然比y方向大,但 x方向的残差反映地面的起伏,这与三组立体像对均位于地势起伏较小的平原、丘陵地区的实际情况是一致的。
2.第一组试验影像为多时相立体像对,由于地物、光照的变化,多时相影像的匹配一般比同期立体像对的匹配成功率低得多。灰度相关方法和SIFT匹配方法,都大约只匹配出15对同名点,而本文的方法则匹配了96对同名点。图4为影像局部三种方法比较结果。可见本文方法获取的同名点非常密集,灰度相关方法只正确匹配2个同名点,而SIFT特征匹配方法未能在该区域匹配出任何同名点。这也从一个侧面表明,虽然SIFT匹配方法可处理影像旋转、缩放、视角变换等一系列变形,但当影像已发生实质变化时,经典的影像相关策略仍表现出更高的稳健性。
3.第二组立体像对视差仅为3天,且光照条件较为一致,因此在3组试验影像中匹配成功率最高。灰度相关方法和SIFT匹配方法的正确匹配点数在200个左右,而本文的方法正确匹配点数为333个。图5为第二组SPOT影像局部区域三种匹配方法的比较。除了匹配点较多外,本文方法匹配的同名点分布较均匀。SIFT匹配方法虽然特征点也较多,但分布不够均匀。
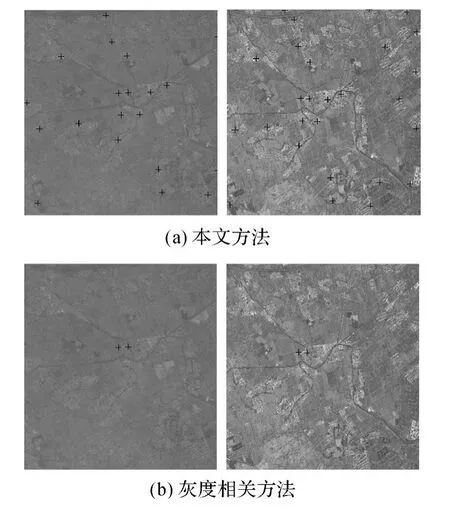
图4 第一组立体影像匹配点的局部放大图Fig.4 Image matching results in part of stereo image S1
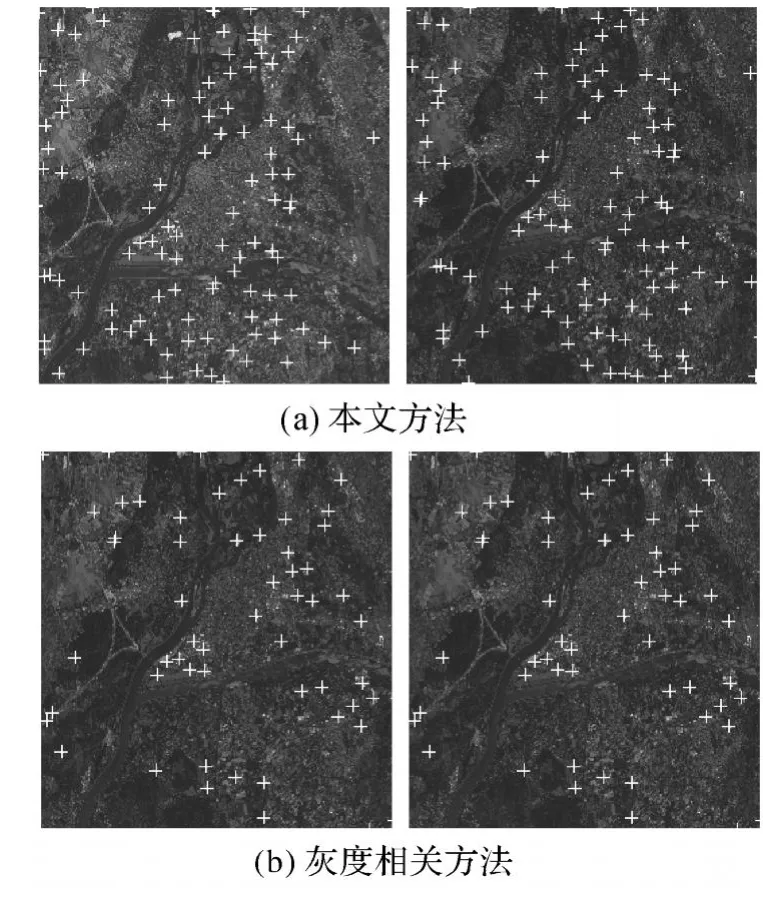

图5 第二组立体影像匹配点的局部放大图Fig.5 Image matching results in part of stereo image S2
4.第三组为QuickBird同轨立体像对,将影像旋转90°后构建近似核线方程再进行匹配。由于核线斜率约为15°,严重影响相关系数计算的有效性,故传统灰度相关算法的匹配成功率是最低的。SIFT算子由于不受影像旋转的影响,因此匹配点数明显高于灰度相关算法。而本文的方法是将匹配窗口进行核线重采样后再进行匹配,保证相关系数计算的有效性,取得了最好的匹配效果。图6为靠近影像中心的某局部区域,可明显看出同轨立体像对存在较大的几何变形。图6(a)为本文方法的匹配结果,该区域共正确匹配出18对同名点,图6(b)为SIFT匹配方法的匹配结果,共匹配出13对同名点。而传统的灰度相关算法未能匹配出任何同名点。
4 结束语
由于拍摄时间变化、姿态角差异、成像机理复杂等问题,高分辨率卫星遥感影像匹配一直存在着匹配率低、可靠性差等问题,实际生产中仍需采用人工选定控制点的方法进行影像配准、模型定向等作业。本文通过引入RPC参数建立基于投影轨迹的近似核线方程,分析同名点预测误差和核线精度,以此为初始条件,进行近似一维影像匹配,并采用RANSAC算法剔除误匹配点,取得了较好的匹配效果。本文针对同、异轨立体成像模式、多时相、大姿态角等情况下拍摄的高分辨率卫星遥感影像,与传统的灰度相关方法和现流行的SIFT匹配算法作比较试验,证明本文的方法具有可靠性好,匹配成功率高的优点。无论是多时相或者大姿态角影像,都可正确匹配出相当数量的同名特征点,用于后继的影像配准、定向、变化检测等作业,而无需再手工测点。
[1] LI Xiaoming,ZHENGLian,HU Zhanyi.SIFT Based Automatic Registration ofRemotely-sensed Imagery [J]. Journal of Remote Sensing,2006,10(6):885-892.(李晓明,郑链,胡占义.基于SIFT特征的遥感影像自动配准[J].遥感学报,2006,10(6):885-892.)
[2] LV Jinjian,WEN Gongjian,LI Deren,et al.A New Method Based on Spatial Relations for Feature Matching[J].Acta Geodaetica et Cartographica Sinica,2008,37(3):367-373.(吕金建,文贡坚,李德仁,等.一种新的基于空间关系的特征匹配方法[J].测绘学报,2008,37(3):367-373.)
[3] ZHANG Dengrong,CAI Zhigang,YU Le.Study on Image Automatism Registration Methods Based on Matching[J]. Journal of Zhejiang University:Engineering Science,2007, 41(3):402-406.(张登荣,蔡志刚,俞乐.基于匹配的遥感影像自动纠正方法研究[J].浙江大学学报:工学版,2007, 41(3):402-406.)
[4] YU L,ZHANG D R,HOLDEN E J.A Fast and Fully Automatic Registration Approach Based on Point Features for Multi-source Remote-sensing Images[J].Computers& Geosciences,2008,34:838-848.
[5] ZHANG Li,ZHANGJixian.Automatic DEM Generation from High-Resolution Satellite Imagery Based on Multiple-Baseline Image Matching[J].Geomatics and Information Science of Wuhan University,2008,33(9):943-946.(张力,张继贤.基于多基线影像匹配的高分辨率遥感影像DEM的自动生成[J].武汉大学学报:信息科学版,2008, 33(9):943-946)
[6] ZHANG L,GRUEN A.Multi-image Matching for DSM Generation from IKONOS Imagery[J].ISPRS Journal of Photogrammetry&Remote Sensing,2006,60:195-211.
[7] OTTO G,CHAU T.Region Growing Algorithm for Matching of Terrain Images[J].Image and Vision Computing,1989,2(7):83-94.
[8] KORNUS W,ALAM U′S R,RUIZ A,et al.DEM Generation from SPOT-5 3-fold along Track Stereoscopic Imagery Using Autocalibration[J].ISPRS Journal of Photogrammetry&Remote Sensing,2006,60(3):147-159.
[9] TAO C V,HU Y.A Comprehensive Study of the Rational Function Model forPhotogrammetric Processing [J]. Photogrammetric Engineering&Remote Sensing,2001, 67(12):1347-1357.
[10] ZHANG Li,ZHANG Jixian,CHEN Xiangyang,et al. Block Adjustment with SPOT-5 Imagery and Sparse GCPs Based on RFM[J].Acta Geodaetica et Cartographica Sinica,2009,38(4):302-310.(张力,张继贤,陈向阳,等.基于有理多项式模型RFM的稀少控制SPOT25卫星影像区域网平差[J].测绘学报,2009,38(4):302-310.)
[11] FRASER C S,HANLEY H B.Bias Compensation in Rational Functions for IKONOS Satellite Imagery[J].Photogrammetric Eng.&Remote Sensing,2003,69(1):53-57.
[12] OpenGIS Consortium.The OpenGIS Abstract Specification (T opic 7:The Earth Imagery Case)[EB/OL].[2001-05-08]. http:∥portal.opengeospatial.org/files/?artifact_id=892.
[13] REINARTZ P,MÜLLER R,LEHNER M,et al.Accuracy Analysis for DSM and Orthoimages Derived from SPOT HRS Stereo Data Using Direct Georeferencing[J]. ISPRS Journal of Photogrammetry &Remote Sensing, 2006,60(2006):160-169.
[14] ZHANG Zuxun,ZHOU Yueqin.Epipolar Line of SPOT Images Using Fitting Method[J].Journal of Wuhan University of Surveying and Mapping Technology,1989, 14(2):20-24.(张祖勋,周月琴.用拟合法进行SPOT影像的近似核线排列[J].武汉测绘科技大学学报,1989, 14(2):20-24.)
[15] JIANG Wanshou,ZHANG Jianqing,ZHANG Zuxun. Simulation of Three-line CCD Satellite Images from Given Orthoimage and DEM[J].Geomatics and Information Science of Wuhan University,2008,33(9):943-946.(江万寿,张剑清,张祖勋.三线阵CCD卫星影像的模拟研究[J].武汉大学学报:信息科学版,2002,27(4):414-419.)
[16] ZHANG Yongsheng,GONG Danchao.Application of High Resolution Remote Sensing Satellites-model,Processing and Application[M].Beijing:Science Publications,2004:86-89.(张永生,巩丹超.高分辨率遥感卫星应用-成像模型、处理算法及应用技术[M].北京:科学出版社,2004:86-89.)
[17] SAKAMOTO M,UCHIDA O,DOIHARA T,et al.Detection of Collapsed Buildings Due to Earthquake in Urban Areas[C]∥ISPRS.Istanbul:[s.n.],2004.
[18] FISCHLER M A,BOLLES R C.Random Sample Consensus:a Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography[J].CACM, 1981,24(6):381-395.
[19] LOWE D G.Distinctive Image Features from Scale-Invariant Keypoints[J].International Journal of Computer Vision,2004,60(2):91-110.
[20] YUAN Xiuxiao.A Novel Method of Systematic Error Compensation for a Position and Orientation System[J]. Progress in Natural Science,2008,18(8):953-963.
(责任编辑:宋启凡)
Automatic Matching of High Resolution Satellite Images Based on RFM
J I Shunping,YUAN Xiuxiao
School of Remote Sensing and Information Engineering,Wuhan University,Wuhan 430049,China
A matching method for high resolution satellite images based on RFM is presented.Firstly,the RFM parameters are used to predict the initial parallax of corresponding points and the prediction accuracy is analyzed. Secondly,the approximate epipolar equation is constructed based on projection tracking and its accuracy is analyzed.Thirdly,approximate 1D image matching is executed on pyramid images and least square matching on base images.At last RANSAC is imbedded to eliminate mis-matching points and matching results are obtained. Test results verified the method more robust and with higher matching rate,compared to 2D gray correlation method and the popular SIFT matching method,and the method preferably solved the question of high resolution satellite image matching with different stereo model,different time and large rotation images.
image matching;epipolar equation;RANSAC;RFM
J I Shunping(1979—),male,PhD,lecturer,majors in image matching and location of high-resolution remote sensing images.
E-mail:jishunping 2000@163.com
1001-1595(2010)06-0592-07
P237
A
国家973计划(2006CB701302);武汉大学自主科研项目(4082004)
2009-12-21
2010-06-02
季顺平(1979—),男,博士,讲师,主要从事高分辨率遥感影像匹配及定位研究工作。

