涌潮荷载作用下大型桁架式平面闸门动力响应仿真分析
严根华,陈发展
(南京水利科学研究院,江苏南京 210029)
涌潮荷载作用下大型桁架式平面闸门动力响应仿真分析
严根华,陈发展
(南京水利科学研究院,江苏南京 210029)
通过三维有限元数值模型进行涌潮荷载作用下大型桁架式平面闸门动力响应仿真分析,研究大型桁架式平面闸门的结构动力特性,得出流固耦合条件下闸门结构的振动频率变化特征。在此基础上,通过涌潮荷载作用模拟对结构的动力响应进行仿真计算,得出闸门动位移和动应力值。采用水弹性振动模型对闸门结构的涌潮动力响应进行试验验证。验证结果表明,仿真计算结果与试验结果基本一致,仿真计算结果合理。最后,针对局部应力集中现象对闸门结构进行修改优化,并提出抗振优化方案。
桁架式平面闸门;流固耦合动力特性;动力响应;仿真计算;试验验证;曹娥江大闸
曹娥江大闸枢纽工程位于钱塘江下游右岸主要支流曹娥江河口,枢纽主要由挡潮泄洪闸、堵坝、导流堤、连接坝段以及管理区等组成,具有防洪(潮)、治涝、水资源开发利用、航运、改善水环境条件等多目标综合效益。曹娥江校核洪水位为6.52m,设计洪水位为6.22m,正常蓄水位为3.90 m,最低水位为3.00m。挡潮泄洪闸闸孔总净宽为560m,设计流量约为11340m3/s,共设28个孔,单孔宽度为20m,底板高程为-0.50m(黄海基面)。挡潮泄洪闸工作闸门采用潜孔式平面滑动闸门,胸墙底高程为4.00m,孔口尺寸为20.0m×4.5m(宽×高)。闸门跨度大,宽高比达4.4,闸门梁系采用空间桁架体系,结构布置见图1~2。

图1 水闸结构布置

图2 闸门结构布置(单位:mm)
按照该枢纽的基本运行要求,挡潮泄洪闸需满足双向挡水要求,对闸门的运行安全性提出了更高的要求。该水闸结构具有如下特点:①工作闸门采用平面桁架结构,宽高比悬殊,其体形系国内外先例;②闸门需局部开启运行;③闸门的许多运行工况为淹没出流;④工作闸门受钱塘江涌潮冲击,闸门将承受很大的涌潮荷载,其动荷载作用是造成闸门强烈振动的振源之一。这种强涌潮对工作闸门产生很大的冲击荷载,是造成闸门强烈振动的又一控制性振源。一旦水动力荷载的作用力特性和闸门结构的固有特征产生不利组合作用,就会造成闸门的危害性破坏。迄今为止,对这种涌潮作用下的结构动力问题研究很少,对涌潮水动力作用机理没有进行过专门研究,更没有结构动力响应及优化设计方面的研究报道。
曹娥江大闸是我国目前规模最大的挡潮闸,结构面临复杂的水动力荷载作用,动力安全问题十分严峻。因此对挡潮泄洪闸涌潮冲击荷载和流激振动特征需要进行深入研究,揭示存在问题,提出抗振安全措施,从而确保挡潮泄洪闸的安全乃至整个大闸的运行安全。笔者通过三维有限元数学模型对闸门结构的动力响应进行仿真分析,并与试验结果进行比较,验证仿真分析结果的合理性和可靠性,为闸门结构安全设计提供依据。
1 闸门结构有限元模型
曹娥江大闸闸门结构的数学模型采用三维有限元法建立,分析软件采用ANSYS10.0。按质量、刚度变化将闸门结构离散为具有 1 900个管单元、3436个板单元、21285个实体单元,合计41764个节点,约有20万个自由度的空间结构体系。计算中采用PIPE20管单元、SHELL63板壳单元和SOLID95体单元,其中,管单元用于桁架结构,板壳单元用于面板、加强肋板和上下弦的连接处,体单元用于矩形管和方管梁结构,闸门有限元模型见图3。板单元质量为22.6 t,体单元质量为32.08t,管单元质量为43.65t,门体总质量为98.3t。

图3 闸门结构有限元模型
2 闸门结构的动力特性
闸门结构的动力特性主要包含结构固有频率、振型等参数,考虑到工程实际运行时闸门受到动水作用而振动,流场对结构固有特性将起到显著影响,因此动力分析时必须考虑水介质对结构动力特性的影响。
2.1 闸门流固耦合振动模态特性分析
在水动力荷载作用下,闸门结构的运动可用以下方程表示[1-2]:

式中:M,C,K分别为质量矩阵、阻尼矩阵、刚度矩阵 ;δ为结点位移向量 ;﹒δ为节点速度向量;¨δ为节点加速度向量;P(t)为动力荷载。
闸门振动必然引起流场压力的波动,水体压力波动又反过来影响闸门结构的振动,是典型的液体和弹性体的流固耦合振动问题。耦合系统自振控制方程可利用第2类Lagrange方程得到,以 p表示水作用于流体作用面有关节点的动水压力向量,可得流固耦合自振特性方程:

其中p满足以下无黏性不可压缩的微幅流体运动拉普拉斯方程:

经推导可得闸门流固耦合自由振动方程为

式中:Mp为附加质量阵;S,T为转换矩阵;D为方阵。
将式(4)转化为如下形式的特征值方程:

式中:Φi为第i阶的振型矩阵;λi为特征值。
此处 Mp是非对称矩阵,因此不能将其转化为标准特征值问题。用于求解非对称特征值问题的方法是Lanczos法。
2.2 计算结果
当闸门处于无水状态,门叶两侧和启闭杆约束下的闸门振动模态分析结果表明,在该约束边界下,闸门的1阶基频为13.6Hz,为整体扭转振型;2阶频率为17.56Hz,为整体弯曲振型;3阶频率为17.8Hz。实际运行时,闸门结构将受到上下游水介质的影响,结构的固有振动特性出现一定程度的变化,尤其是结构的固有频率会有较大下降。计算时流场范围取10倍闸门高,图4为闸门开启状态下考虑水体影响的第1~6阶模态振型示意图。计算结果表明,考虑流固耦合作用时,闸门结构的 1阶固有频率为6.6Hz,为面板1阶弯曲振型;2阶振型为面板2阶弯曲,相应频率为7.7Hz;3阶固有频率为10.4Hz,为面板与桁架空间组合变形振动。显然,闸门结构的1阶基频较不考虑水体影响时下降了51%。由此可知,流场对结构的动力特性影响非常显著,不能忽视。
3 闸门结构的静力特性
闸门结构的静力特性是安全性评价应当掌握的重要评估资料。工程结构的破坏除动力作用破坏外,静力失效也是常见现象。因此,在对水闸进行动力分析的同时,开展闸门结构的静力特性研究亦是十分必要的。通过对闸门结构的位移和应力分布研究可为结构的体形设计提供科学依据。
闸门处于挡水工况,水位为校核洪水位时,总水压力(反力)为5 003.9kN。此时闸门最大位移为13.579mm,发生在面板底缘中心位置。闸门结构的最大应力出现在桁架结构∅530mm圆管末端,最大应力值达到267MPa,图5~6给出了闸门整体位移及应力分布。挡潮工况下闸门结构的应力与位移量略小。当下游水位为8m、上游水位为3.3m时,闸门总水压力为 4 704.6 kN。此时闸门最大位移为10.36mm,出现在闸门中断面的底缘部位;最大应力为203MPa,位于桁架结构∅530mm圆管末端;桁架管系弓形管外侧节点应力为59MPa。该工程闸门采用Q345钢,容许应力为220MPa,校核工况下闸门出现最大应力集中区,需要局部修改和优化。
4 涌潮荷载作用下闸门结构瞬态响应分析
4.1 流激振动响应仿真计算基本理论
考虑闸门结构流固耦合相互作用,水动力荷载作用下的闸门结构振动可用离散化线性微分方程表示为

图4 流固耦合状态下闸门结构低阶模态振型

图5 校核水位闸门整体位移(单位:mm)

图6 校核水位闸门整体应力及局部应力(单位:Pa)

式中:MS,CS和KS分别为流体耦合附加质量、附加阻尼和附加刚度矩阵;MP,CP和KP分别为结构质量、阻尼和刚度矩阵,﹒u 和 u 分别为结构振动加速度、速度和位移列阵;F(t)为外荷载列阵。
经推导,可得任一节点k的位移响应历程为

式中:q为模态阶数;n为结构自由度数;φkj,φij为振型系数;h为脉冲响应系数;t-θ为时间增量;pi(θ)为节点i所受的力。
k点的位移自相关函数可表示为

式中:E为方差;uk(t)和uk(t+τ)分别为t时刻和t+τ时刻节点k的位移;Rp为作用力自相关函数。
对式(8)进行Fourie变换,可得节点k的位移谱密度为
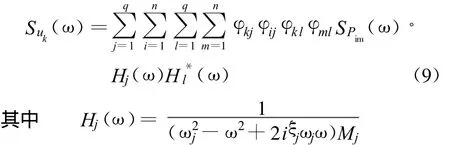

4.2 仿真计算结果
涌潮荷载作用下闸门结构的瞬态响应分析主要考查在钱塘江涌潮作用下闸门结构的动应力和动位移变化情况,评价闸门结构的动力安全状况。根据历史涌潮过程确定最大涌潮压强为90kPa。

图7 闸门后桁架下部上弦管典型中间节点的位移响应过程线
按闸门关闭状态考虑:鉴于涌潮作用力具有典型冲击特征,因此将涌潮作用力用脉冲荷载进行模拟,幅值为90kPa,作用力范围覆盖闸门整个面板。图7给出了闸门结构在关闭状态受到冲击荷载作用下第20ms时闸门后桁架下部上弦管典型中间节点的位移响应过程线。闸门结构的应力分布显示,在受到涌潮冲击20ms后,闸门最大应力值位于桁架结构∅530mm圆管末端,最大应力值为620MPa,桁架管系弓形管外侧节点应力为160MPa。图8给出了冲击荷载作用下第25ms时的闸门整体应力(迎水面)分布云图。闸门最大位移为20.37mm,位于闸门中断面处。当闸门受到涌潮冲击52ms时,闸门最大应力为455MPa,仍然位于桁架结构∅530mm圆管末端;桁架管系弓形管外侧节点应力为194MPa;闸门最大位移为22.4mm。图9为闸门在冲击荷载作用下第50ms的整体位移(迎水面)。闸门结构的应力分布显示,在目前的模拟涌潮冲击荷载作用下,在受涌潮冲击52ms时,桁架结构∅530mm圆管末端的最大应力小于冲击时间为20ms时的应力,但桁架管系弓形管外侧节点应力大于冲击时间为20ms时的应力。说明结构部位不同,出现最大位移和应力的时间也有相应变化。动力响应数据显示,在设计冲击荷载作用下,门体的应力分布出现应力集中现象,并远超过闸门的容许应力,需要采取适当措施。应当指出,因仿真计算采用线性模型,导致计算值超过600MPa,此时闸门结构已进入非线性区,并超过材料的屈服应力点。

图8 闸门结构在冲击荷载作用下第25ms时的整体应力(迎水面)(单位:Pa)

图9 闸门在冲击荷载下第50ms时的整体位移(迎水面)(单位:mm)
4.3 闸门动力响应模型试验验证
结构动力响应计算获得了涌潮荷载作用下的结构应力和位移响应数据,以及结构动力安全评价资料。为验证计算结果的正确性,采用水弹性模型进行试验验证。水弹性振动模型严格按照水弹性相似原理要求采用特种材料制作,其中质量密度ρr和材料弹性模量Er分别满足

式中:Lr为模型几何比尺。
闸门水弹性振动试验结果表明,工作闸门在涌潮荷载冲击下出现瞬间最大冲击振动位移,随后出现低频振荡衰减[3]。从振动位移量看,门体跨中的动力响应比两侧的大。例如,在涌潮高度为3.6m、潮头流速为4.95m/s的涌潮冲击下,门体跨中中部顺水流向测点的最大振动位移为21.33mm,横河向最大振动位移为3.23mm。门体跨中下部顺水流向测点的最大振动位移为26.96mm,垂向最大振动位移为4.58mm。在闸门1/4宽度处的下部1号测点处,顺水流向测点的最大振动位移为17.86mm,横河向测点的最大振动位移为7.27mm。
当涌潮高度为5.0m时,门体顺水流向最大振动位移为23.24 mm,横河向最大振动位移为7.98mm,垂向最大振动位移为5.39mm。其他水位、涌潮高度、潮速组合条件下的闸门振动位移响应值一般在22~26mm之间。通过与试验数据的对比分析可知,有限元计算得到的涌潮冲击位移量与模型试验值基本一致,说明计算结果是合理的。
5 闸门结构的优化修改
由前述计算成果可知,在正常挡水或挡潮工况下,最大位移量为13.58mm,出现在闸门中断面的底缘部位;闸门结构的最大应力出现在桁架结构∅530mm圆管末端,为 267MPa。从刚度角度看,闸门的位移量满足规范要求[4]。
涌潮荷载作用下闸门结构瞬态响应分析结果表明:在设计给定的荷载作用下,闸门结构在受到涌潮冲击初期,闸门出现最大冲击应力为620MPa,位于桁架结构∅530mm圆管末端,桁架管系弓形管外侧节点应力为160MPa;闸门最大位移为20.37mm,位于闸门中断面处。随后出现衰减振荡,桁架结构圆管末端应力下降为455MPa,弓形管外侧节点应力为194MPa;闸门最大位移值为22.4mm。结构的应力分布显示,在设计冲击荷载作用下,闸门应力分布出现严重的应力集中现象,需要采取适当措施。
根据原方案闸门结构受力情况分析,闸门结构的应力控制工况是涌潮作用工况,因此对涌潮冲击荷载作用下的结构做如下修改:把桁架∅530mm圆管末端连接板的厚度由25mm加大为40mm;加大弓形圆管末端连接板的厚度,其中底肋板、立肋板、斜肋板及其余支撑肋板的厚度由25 mm分别改为40mm,50mm及60mm;所有矩形管xb1和方管xb2的连接处增加加强斜肋板,其尺寸为200 mm×111.8mm×25mm。
通过上述修改,闸门结构在涌潮作用下(最大瞬态冲击压强为0.09MPa)的瞬态响应约束反力为9793.5kN。闸门结构的最大位移为24.0mm,最大涌潮冲击应力为156MPa。显然闸门结构修改后的应力已经下降至容许应力范围,取得了满意的抗振效果。
6 结 语
对相位差不很突出的冲击荷载作用而言,通过构建数学模型,可以进行结构动力响应参数的预测和分析。本文研究获得以下几点结论:
a.对该工程闸门而言,流场对闸门固有特性产生显著影响,最大频率下降率达51%,动力响应计算时必须加以考虑。
b.对于桁架式结构来说,涌潮冲击荷载作用下力的传递由闸门中部的桁架杆系向二侧拱脚传递,应力集中点出现在弓形圆管末端应力量级远超过材料的屈服极限,需要对结构进行局部修改优化。
c.涌潮冲击响应模型试验取得了闸门关键部位的位移和应力分布数据,其结果与仿真计算值基本一致,验证了仿真计算结果的合理性。
d.优化修改后的闸门结构动力响应仿真计算结果显示,在相同涌潮荷载作用下,推荐方案最大应力集中区消失,最大应力由620MPa下降为150MPa,取得了满意的抗振效果。
[1]古华,严根华.水工闸门流固耦合自振特性数值分析[J].振动测试与诊断,2008,9(3):242-246.
[2]YAN Gen-hua.Study of design techniquesfor dynamic safety of radialgates in hydraulic engineering[C]//Structure Engineering World Wide.San Francis:Elseview Science Ltd.,1998.
[3]严根华,陈发展.曹娥江大闸枢纽工程闸门流激振动试验研究[R].南京:南京水利科学研究院,2006.
[4]DL/L5039—95 水利水电工程钢闸门设计规范[S].
Simulation of dynamic responses of large truss-plane gates under tidal surge loads
YAN Gen-hua,CHEN Fa-zhan(Nanjing Hydraulic Research Institute,Nanjing210029,China)
The dynamic responses of large truss-plane gates under tidal surge loadswere simulated by means of three-dimensional finite element numerical models.The structural dynamic characteristics of the large truss-plane gates were studied.The variation characteristics of the vibration frequency of the gates under fluid-solid coupling conditions were obtained.On such a basis,the structural dynamic responses were calculated through the simulation of tidal surge loads,and the dynamic displacement and stress of the gates were obtained.The dynamic responses of the gates under tidal surge loads were verified by means of hydro-elastic vibration models.The test results show that the numerical simulations agree with the experimental results,indicating the numerical simulations are rational.Finally,for the local stress concentration phenomenon,the gate structure was modified and relevant optimization scheme was proposed.
truss-plane gate;fluid-solid coupling dynamic characteristic;dynamic response;simulation calculation;experimental verification;Caoe River Sluce
TV663
A
1006-7647(2010)03-0042-05
10.3880/j.issn.1006-7647.2010.03.011
严根华(1956—),男,上海人,教授级高级工程师,从事水工水力学及结构流激振动研究。E-mail:ghyan@nhri.cn
2009-07-13 编辑:骆超)

