一种属性选择方法FS-IV的研究

杨秋洁, 胡学钢

(合肥工业大学计算机与信息学院,安徽合肥 230009)

信息技术的高速发展使数据分析需要处理的信息量产生了爆炸式增长,特别是近年兴起的数据流领域研究,对分类模型的实时性提出了更高要求。在实际应用中,由于数据分布多样、属性冗余且包含噪音,传统的分类技术易出现过拟合及时空开销过高等问题。因此,在保证分类精度的前提下,适当约减属性维数、降低数据规模,即进行属性选择成为可行的办法。

在数据挖掘应用领域,常见的属性选择方法有 Relief、PCA(Principal Components Analysis,简称PCA)、One-R、粗糙集合和信息熵等。Rilief是一种基于统计相关性标准选择属性的方法,通过对实例集合抽样而计算出每一个属性的权重来选择属性[1],该方法能选择出相关性较强的属性,并能处理离散和连续的属性,然而对于冗余属性的去除效果不理想;PCA方法[2]研究了各个统计变量之间的相互关系,尝试用较少的新变量代替原来较多的变量,并尽可能多地保留原来变量反映的信息,由于它选取的属性是利用数据相关矩阵运算得到的,满足属性相互正交但无法保证相互独立,且多用于连续型属性选择,计算复杂度较统计方法高;粗糙集合方法[3]试图在保持属性对目标分类能力的前提下,淘汰冗余属性,可以有效地删除冗余及不相关属性,然而由于分辨矩阵及属性重要度的求解都需要大量计算,难以满足实时性要求高的场合;信息熵类方法[4]是通过计算信息熵来评价属性重要度从而进行属性选择,由于每次选择都需要重新计算各维属性的排序,随着数据量的增加,时间开销较大;One-R[5]是利用每个属性的分类正确率进行排序选择,时空性能较佳,但当各属性关联性较强时,One-R方法则不具有较好的区分度。

针对上述经典属性选择方法对高维海量数据存在的计算复杂度高、时间性能不佳或区分度不明显等问题,本文将数学分析中的IV指标作为属性选择的评价标准,提出FS-IV属性选择算法,仅需一遍扫描计算出所需的相关统计量,由大量实验得出的经验阈值来评估属性重要程度[6,7]。实验表明,FS-IV属性选择方法时空性能良好,对冗余、噪音属性均有较好的区分能力,能够有效地约减数据规模。

1 IV指标

IV指标(information value,简称 IV)[6,8]作为一种数学理论在20世纪50年代被首次提出,主要用于概率论中分析各因子对结果的影响情况。近年来,由于它在数据分析方面表现优良,尤其在信用卡评分领域,可以很好地评价各项指标对用户信用状况影响的重要程度,得到了广泛应用,与IV相关的定义如下。

定义 1 Woe值(Weight of evidence,简称Woe)[8,9]：对于属性 X的取值xi、类别Y=yk和Y≠yk时,信息熵值上的差别可以理解为属性取值为xi对最终分类为yk所做贡献的度量,因此将这种差别定义为贡献度权重(Woe)[7],记为Woe(xi,yk)：

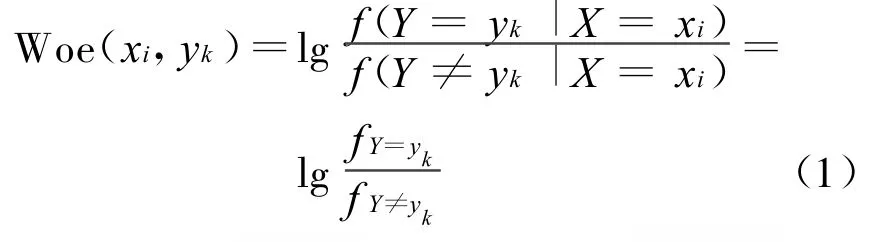
其中,f(Y=yk|X=xi)、f(Y ≠yk|X=xi)表示属性X=xi时,分类标签为Y=yk及y≠yk的概率值或概率密度函数。考虑到实际应用中可能出现某属性值下分类为yk的实例为零的情况,即f(Y=yk|X=xi)=0,为避免造成分母为零导致Woe取值趋于无穷大造成过拟合现象,在此约定取实例数为1计算。属性值xi对Y=yk起正向作用,其 Woe值为正,反之为0或负值[7]。

定义2 IV指标：根据(1)式计算出的Woe值可以进一步计算IV指标,即

其中,f(Y=yk)、f(Y ≠yk)为属性X=xi时,Y=yk和Y≠yk的条件概率密度,若是离散属性,则统计其概率取值。实验表明[10],IV的经验值与对应意义分别如下：[0,0.02],该属性几乎没有贡献度;[0.02,0.1],该属性贡献度较低;[0.1,0.3],该属性贡献度中等;[0.3,无穷],该属性贡献度非常高。

2 算法描述

2.1 IV属性评价标准

通过研究IV指标的数学模型,得出如果将IV引入属性选择,将具有如下优势：

(1)IV的指标有较为普适的阈值来决定究竟哪些因素起了最主导的作用,而其它多数属性选择指标通常只能够对影响力大小排序,不易确定选用多少属性可以达到较满意的效果。

(2)IV计算快速,时空开销小,适合进行数据预处理。

基于上述考虑,本文尝试将IV引入属性选择,提出了基于IV的属性选择方法FS-IV。

2.2 基于IV的属性选择算法FS-IV

算法描述如下：①读入一个窗口大小的训练数据量;②对每个属性 Xi,统计类标号为yk时,属性Xi取值为j的计数值CountXijk;③若未读完全部数据,则回到步骤(1),否则继续;④由CountXijk计算Xi取值为j时的Woe值Woe(xij,yk);⑤对每个属性Xi,根据各Woe(xij,yk)值,计算IVi;⑥设总属性维数为M,取所有IVi∈[0.3,+∞)的属性Xi为候选集S;⑦输出候选集S。

3 实验及分析

实验分为以下几个部分：属性评价标准采用IV指标的属性选择方法FS-IV与传统属性选择方法的性能比较;将FS-IV方法应用于多个分类模型IV-RF、IV-NB和IV-C4.5;在易产生过拟合数据集

上的性能比较以及在入侵检测数据上的性能比较[11]。通过上述实验对FS-IV的时空性能进行比较,对IV属性选择方法的有效性进行验证。

3.1 FS-IV时空性能实验

在实验中,使用了LED数据生成器产生的数据集作为属性选择方法性能比较的训练数据集,该数据集有24维属性,其中前7维为有效属性,数据量10×104条,噪音率10%。

与几种常用属性选择方法进行比较,实验结果见表1所列。

表1 FS-IV与经典属性选择方法的对比

从表1可以看出,几种方法均能选择出前7维属性,但排序并不相同。图1所示为时间与空间的性能对比。

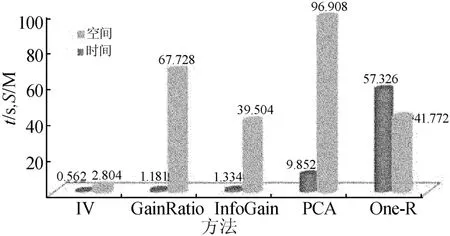
图1 FS-IV与经典属性选择方法的时空性能比较

从图1中可以看出,FS-IV方法的时间性能方面为InfoGain和GainRatio这2个信息熵类方法的1/2,远好于PCA和One-R方法,这是由于FS-IV方法只需要记录每个属性取值的统计信息,可以在读入数据的同时进行统计,不需要保存数据,统计工作完成即可抛弃。在实际操作中,采取了窗口机制,因而空间开销远小于其它几种方法,并适合拓展到数据流领域。

3.2 FS-IV的有效性实验

将多种经典分类算法应用于FS-IV约减后的数据集,以检验FS-IV算法的有效性,表2所列的实验结果使用的是某人口统计数据,共16维属性,缺失值和冗余属性较多,采用FS-IV属性选择方法共选择出来10维超过阈值的属性,为了检验属性选择的效果逐次剔除2维IV值最低的属性,并用C4.5、朴素贝叶斯(NB)和随机森林(RF)3大类方法进行实验。由表2可以看出,随着属性的不断剔除,分类精度逐渐上升,但当剔除了2维高于阈值的属性后,即仅采用8维所选属性时,分类精度又出现了下降,当采用高于阈值的全部10维属性时,各分类器精度达到最佳。FSIV在不同约减维数下的性能对比,如图2所示。

表2 RF与C4.5、N B在不同属性维数下的对比

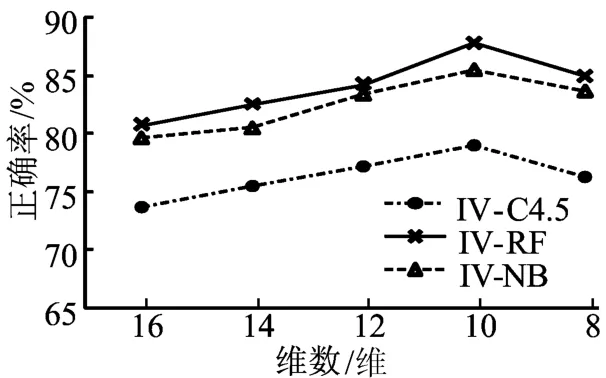
图2 FS-IV在不同约减维数下的性能对比

表3所列的实验结果采用噪音率为10%的LED数据集,由FS-IV属性选择方法从24维属性中选出7维高于阈值的属性,在约减后的数据集上运用C4.5等分类方法检验属性选择的效果,不同分类模型在FS-IV属性选择前后的时间性能对比,如图3所示。

由表3和图3可以看出,在经过约减的数据集上,各分类器精度几乎没有损失甚至略有提高,说明FS-IV方法不仅能够选择出对分类结果最重要的属性,而且还具有一定的抗噪性,而且由于数据规模的大大减小,分类的时间开销也大幅度下降。

表3 FS-IV属性选择前后的正确率对比 %

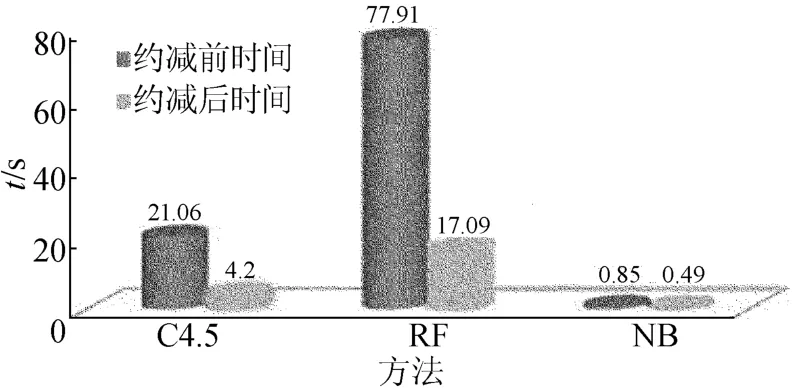
图3 时间性能对比

4 结束语

本文通过引入IV指标进行属性维数约减,提出了FS-IV算法,并与经典分类模型结合,在相同数据集上检验属性选择改进分类模型的效果。实验结果表明,该算法大幅提升了分类模型的时间性能,避免了属性约减造成的分类精度下降等问题,取得了令人满意的效果。FS-IV在计算时采用了增量式方法,时空性能较其它属性选择方法有明显优势,同时,实验表明采用FS-IV的分类模型在保持精度的情况下,均减少了时间开销,并且具有一定的抗噪性,因而适合处理高维、实时性要求高的数据。

由于时间所限,FS-IV算法在更大规模数据上的性能有待进一步验证,如何将FS-IV方法与经典分类算法有机结合从而处理高维数据流领域的问题,是下一步研究的目标和方向。

[1]Kira K,Rendell L.The feature selection problem：traditional methods and a new algorithm[C]//Proceedings of the Ninth National Conference on Artificial Intelligence.New Orleans：AAAI Press,1992：129-134.

[2]Wang Wei,Battiti R.Identifying intrusions in computer networks with principal component analysis[C]//Proceeding s of the First International Conference on Availability,Reliability and Security(A RES'06),2006：66-71.

[3]Zainal A,Maarof M A,Shamsuddin S M H.Feature selection using rough set in intrusion detection[C]//IEEE TENCON 2006,Hong Kong,2006：17-19.

[4]Quinlan J R.C4.5：prog rams for machine learning[M].San M ateo,California ：Morgan Kaufmann,1993：27-33.

[5]Holte R C.Very simple classification rules perform well on most commonly used datasets[J].Machine Learning,1993,11(1)：63-90.

[6]Osteyee D B,Good I J.Info rmation,weight of evidence,the singularity between probability measures and signal detection[M].Berlin：Springer-Verlag,1974：48-76.

[7]Wang Y,Wong A K C.From association to classification：inference using weight of evidence[J].IEEE T ransactions on Knowledge&Data Engineering,2003,15(3)：33-38.

[8]Kullback S.Information theory and statistics[M].New York ：Wiley,1959：18-24.

[9]Good I J.Probability and the weighting of evidences[M].London ：Charles Griffin,1950 ：96-112.

[10]M oez H,Alec Y C,Ray F.Variable selection in the credit card industry[C]//NESUG,2006：61-65.

[11]胡学钢,李 楠.基于属性重要度的随机决策树学习算法[J].合肥工业大学学报：自然科学版,2007,30(6)：681-685.