CFRP布加固混凝土梁裂缝宽度计算方法
谭 军,郑文忠,王 英
(1.哈尔滨工业大学土木工程学院,哈尔滨150090,hitwzzheng@163.com;2.中国建筑科学研究院,北京100013)
试验证明,混凝土受弯构件底部粘贴CFRP布,不仅可提高抗弯承载力,还可有效减小其弯曲裂缝的间距和宽度,改善其正常使用阶段性能[1-3].目前,针对用CFRP布加固梁受弯承载能力的研究较多,而对其裂缝间距和裂缝宽度计算方法的研究较少[4-5],我国2003年颁布的《碳纤维片材加固修复混凝土结构技术规程》(CECS 146:2003)也未对此进行规定.
庄江波等[6]对CFRP布加固混凝土梁的裂缝宽度计算方法进行了研究,根据传统的钢筋混凝土裂缝宽度计算理论,提出了与《混凝土结构设计规范》(GB 50001 2002)(简称《规范》)中普通钢筋混凝土梁裂缝宽度计算方法形式相近的裂缝间距和裂缝宽度计算公式(见式(1)和式(2)).该方法在计算平均裂缝间距时,考虑了受拉CFRP布的影响,在计算受拉钢筋有效配筋率时,将受拉钢筋面积用(As+Acf)代替;在计算平均裂缝宽度时,调整了钢筋应力不均匀系数的计算公式,引入了CFRP布的影响项.该方法计算简便,适用于设计验算.
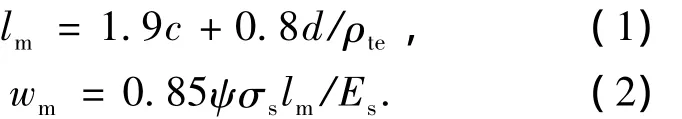
式中:c为最外层纵向受拉钢筋外边缘至受拉区底边的距离(mm);ρte为受拉钢筋有效配筋率,ρte=(As+Acf)/Ac,Ac=0.5bh+(bf-b)hf;d为受拉钢筋直径;σs为裂缝截面钢筋应力;Es为钢筋弹性模量;ψ为钢筋应力不均匀系数,ψ=1.1-0.65ft/[σsρte(1+0.415Acf/(As+Acf))].
本文一方面基于粘结-滑移理论,对CFRP布加固混凝土梁的裂缝间距和宽度公式进行推导,提出了适用于计算CFRP布加固钢筋混凝土梁和有粘结预应力混凝土梁裂缝宽度的理论计算方法,另一方面又按照传统钢筋混凝土结构裂缝分析思路,在平均裂缝宽度lm计算公式中引入CFRP布和有粘结预应力筋影响项,在裂缝宽度wm计算公式和钢筋应力不均匀系数ψ的计算公式中引入考虑CFRP布和有粘结预应力筋作用的影响系数δf,并给出相应半理论半经验公式.经计算,上述两种分析方法的计算结果与试验结果吻合较好.
1 理论分析方法
基本假定:
1)钢筋材料采用理想弹塑性模型[7].
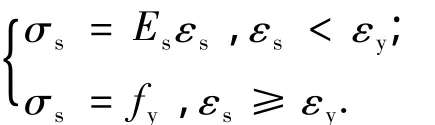
2)受压混凝土的应力-应变关系如图1所示.开裂前,受拉混凝土应力-应变关系保持为线性;开裂后,认为混凝土完全退出工作.取受拉混凝土的弹性模量=Ec/2,Ec为受压混凝土的弹性模量.
3)CFRP布的应力-应变关系为σcf=Ecfεcf.CFRP布与梁底混凝土之间的粘结滑移关系采用陆新征[8]所提出的双线性简化模型
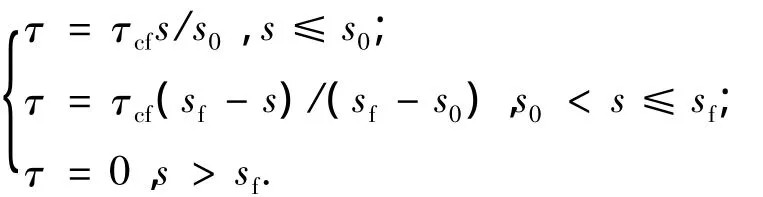
式中:τcf为粘结强度,τcf=1.5 βwft;s0为与τcf对应的滑移值,s0=0.019 5 βwft;sf为粘结应力退化为0的滑移值;βw为CFRP-混凝土宽度影响系数
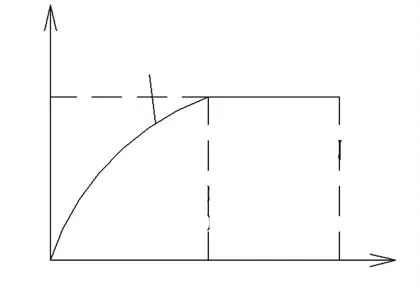
图1 受压混凝土应力-应变关系
4)如图2所示,在纯弯段,开裂截面为1-1,两条相邻裂缝之间的中心截面为0-0,开裂截面与中心截面间距为l.在0-0截面,CFRP布应变εcf(0)与梁底混凝土应变εct(0)相等,二者界面粘结应力τcf(0)=0,混凝土达到最大拉应力;在1-1截面,混凝土的拉应力完全释放σct(l)=0,混凝土退出工作,而CFRP布的拉应力达到最大值σcf(l)=σcf,max,界面粘结应力也达到最大值τcf(l)=τcf,max.沿x方向,0-0截面与1-1截面间各截面的混凝土应变εct(x)逐渐减小,即εct<0,CFRP布应变εcf(x)和受拉钢筋应变εs(x)逐渐增大,即εcf>0,εs>0.
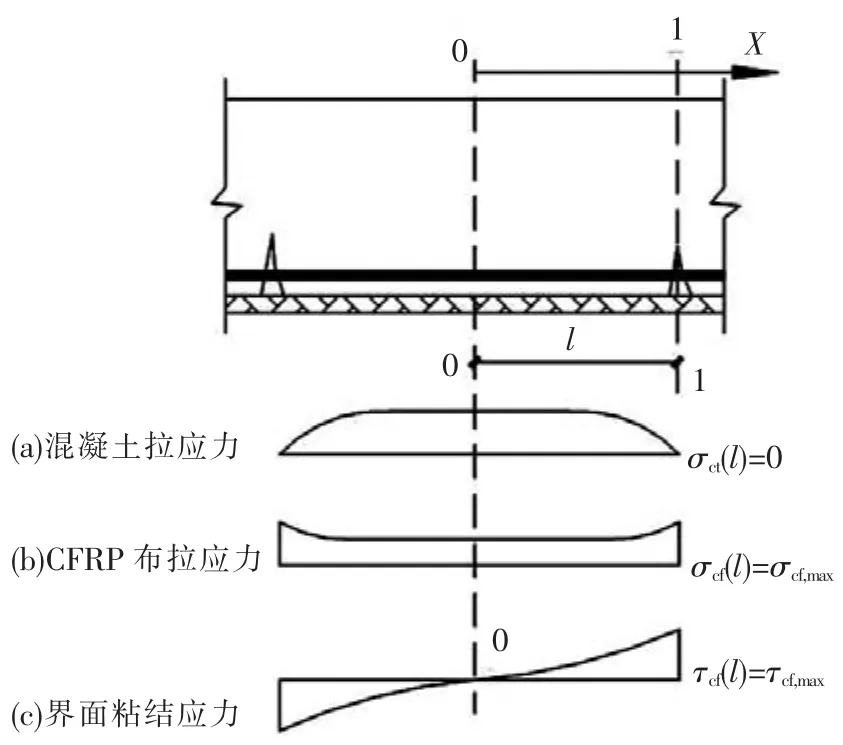
图2 纯弯段两条相邻裂缝计算模型
本文以CFRP加固有粘结预应力混凝土梁为例,进行理论推导.借鉴文献[9]的分析思路,首先建立加固梁开裂截面1-1与相邻即将开裂截面0-0之间任意微元的力平衡方程N(x),然后分析CFRP布与梁底混凝土粘结应力的变化规律.
1.1 粘结应力分析
如图3所示,取开裂截面1-1与相邻即将开裂截面0-0之间任意微元为研究对象,建立力平衡方程:
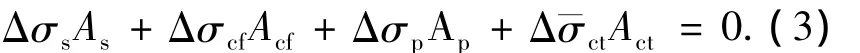
式中:σs为非预应力受拉钢筋应力增量;σcf为CFRP布应力增量;σp为预应力筋应力增量ct为受拉混凝土平均应力增量;As为非预应力受拉钢筋截面面积;Acf为CFRP布计算截面面积;Ap为预应力筋截面面积;Act为受拉混凝土截面面积.
考虑到应变增量很微小,由平截面假定和图4所示几何关系可得到
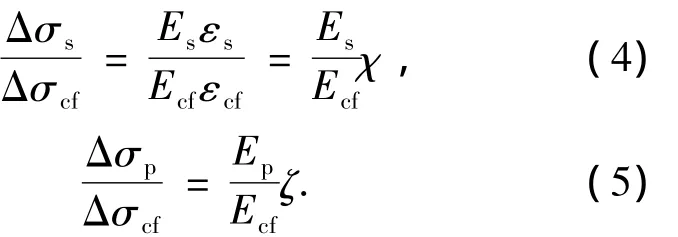
式中:χ=(h0-y)/(h-y),ζ=(hp-y)/(h-y),y为中性轴到梁顶面的距离;Es为非预应力受拉钢筋弹性模量;Ecf为CFRP布弹性模量;Ep为预应力筋的弹性模量.
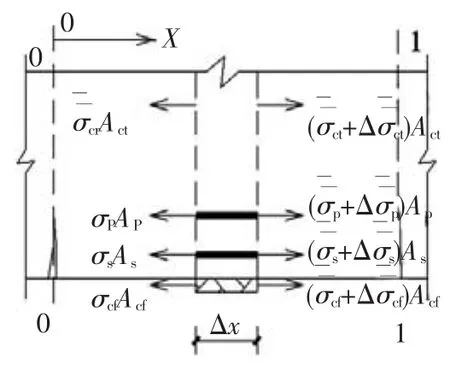
图3 微元体的力平衡条件
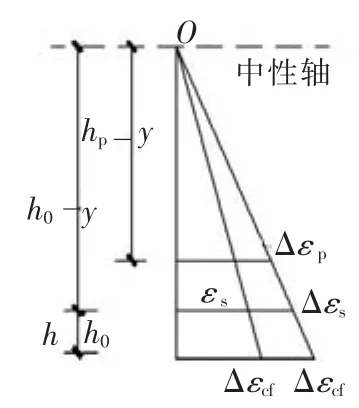
图4 几何关系
根据受拉混凝土应力应变关系可得
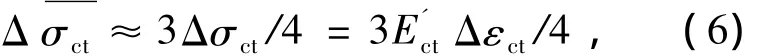
式中:Δσct为受拉区边缘混凝土的应力增量;εct为受拉区边缘混凝土的应变增量.
根据假定(2),E′ct取为Ec/2.将式(4)~(6)带入式(3),移项化简后得
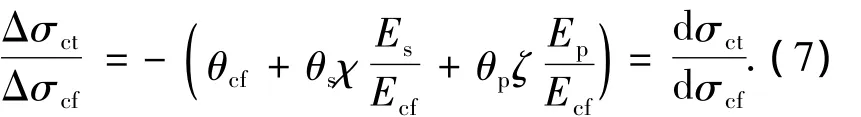
式中:θcf=1.33Acf/Act;θs=1.33As/Act;θp=1.33Ap/Act.
CFRP布与梁底混凝土之间的粘结应力如图5(c)所示.对于长度为x的微元体,由粘结层传递给CFRP布的粘结应力τcf(x)有如下关系:
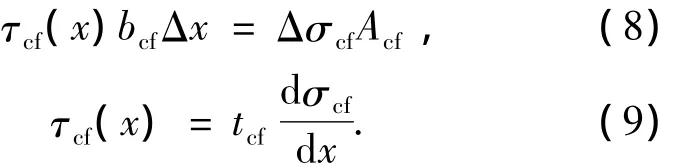
式中tcf为CFRP布的计算厚度.
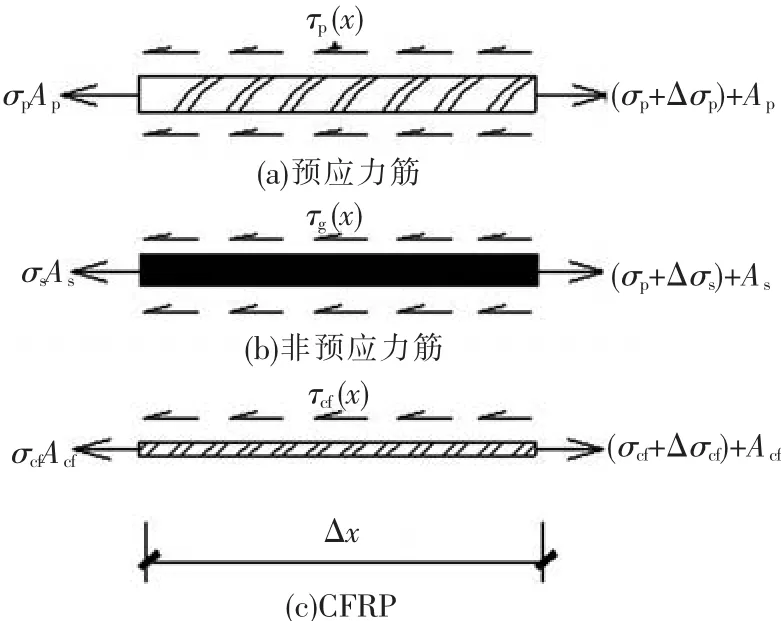
图5 粘结应力
根据假定(4)中的粘结-滑移关系,考虑到裂缝开展的过程中,粘结应力τcf(x)的发展为单调增加,因此仅应用双折线模型的上升段.将τcf和s0的计算结果代入粘结应力公式,得

式(10)等号两边对x求导,整理后得
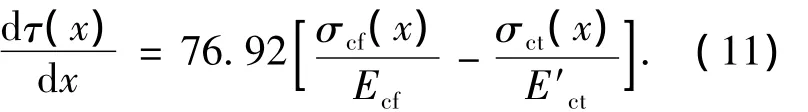
式(11)等号两边同时对x求导,得
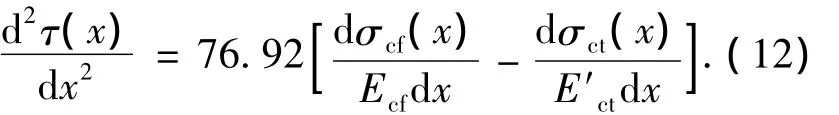
将式(7)和(9)代入式(12),简化后得
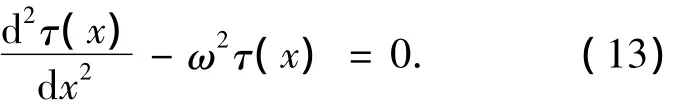
令 μ=(θcf+θsχEs/Ecf+θpζEp/Ecf),则
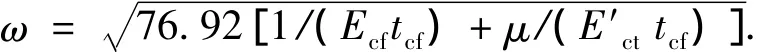
根据已知的边界条件,解上述二阶微分方程,最终得到CFRP布与梁底混凝土之间的粘结应力为
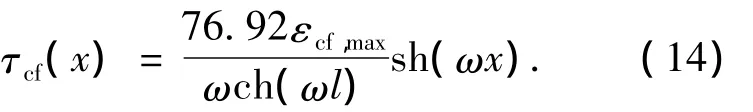
2.2 裂缝间距分析
同样,基于粘结-滑移理论对裂缝开展情况进行分析.将式(14)代入式(9),积分得
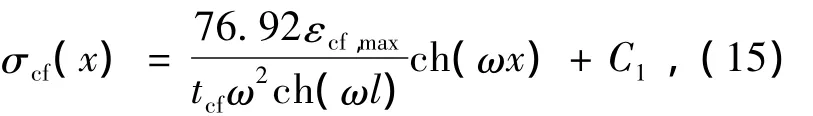
式(7)等号两边同时除以dx,积分得
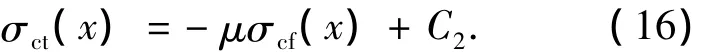
由边界条件 σcf(l)=Ecfεcf,max,σct(l)=0,计算得到实常数C1和C2,代入式(15)整理后得
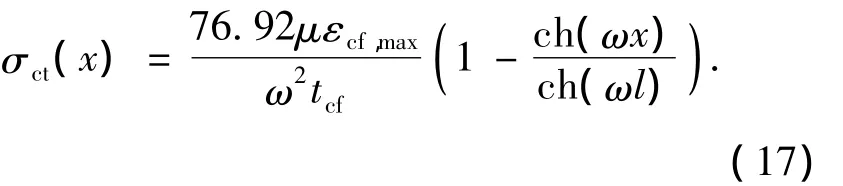
根据假定(4),图2中截面0-0,x=0,CFRP布与梁底混凝土之间相对滑移为零,二者应变相同,混凝土拉应力最大,则有
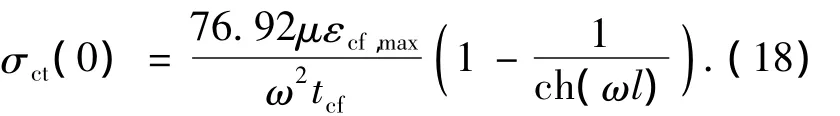
在两相邻裂缝之间若不出现新裂缝,则在两相邻裂缝之间的任意截面应满足σct(0)<ft,整理后得
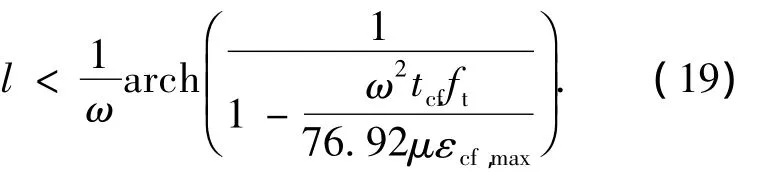
取最大裂缝间距lmax=2l.
2.3 裂缝宽度分析
梁底混凝土的裂缝宽度可表示为梁底面裂缝间距范围内CFRP布与梁底混凝土应变差的积分.则最大裂缝宽度为
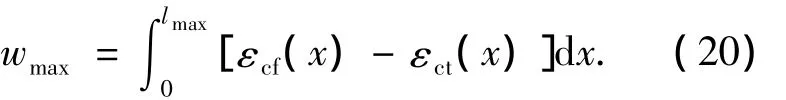
将式(11)和式(14)代入式(20),得到短期荷载作用下,混凝土最大裂缝宽度为
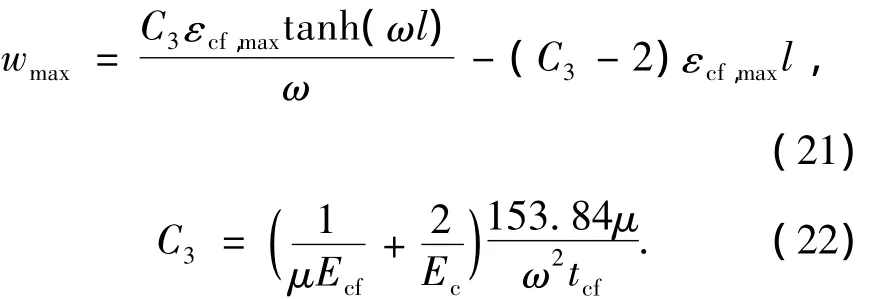
按《混凝土结构设计规范》(GB 50001 2002)(简称《规范》)规定,将长期荷载下裂缝宽度扩大系数暂取为1.5,则可得到CFRP加固混凝土梁按荷载效应标准组合并考虑长期作用影响的最大裂缝宽度.
由于无粘结梁应变沿梁高变化不符合平截面假定,其预应力筋的应力增量计算参照文献[10].将上述各式预应力项去除,即为钢筋混凝土梁裂缝计算方法.
2 实用计算方法
2.1 裂缝间距
按传统钢筋混凝土结构裂缝分析方法进行分析,分别考虑受拉非预应力钢筋、预应力钢筋和CFRP布对裂缝开展的约束作用.
图6中σp为开裂截面处的预应力筋应力;σs为非预应力筋应力;σcf为CFRP布应力;即将开裂截面的应力增量分别为Δσp、Δσs、Δσcf;τp为预应力筋与混凝土之间的粘结强度;τs为非预应力筋与混凝土之间的粘结强度;τcf为CFRP布与梁底混凝土之间的粘结强度.
对图6(a)所示的预应力筋隔离体有
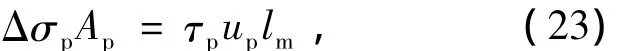
对图6(b)所示的非预应力受拉钢筋隔离体有
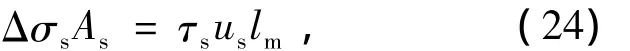
对图6(c)所示的CFRP布隔离体有
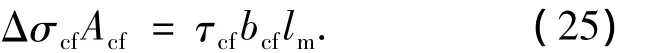
式中:up为预应力筋束的周长;us为钢筋的周长;bcf为CFRP布的粘贴宽度.
混凝土截面开裂弯矩Mcr=Aftkηch,根据弯矩平衡条件:
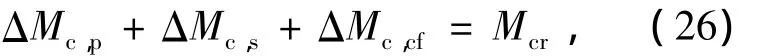
令ΔMc,s/ΔMc,cf=α,ΔMc,p/ΔMc,cf=β,则有
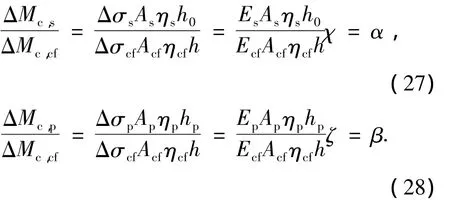
将式(23)~(28)整理后可得
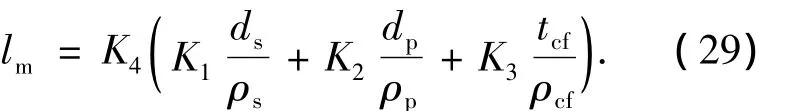
式中:K1=α/(4τsηsh0),K2=β/(4τpηphp),K3=1/(τcfηcfh),K4=ftkηch/(1+α+β),ηsh0,ηphp,ηcfh,ηch分别为非预应力筋、预应力筋、CFRP布、有效受拉混凝土形心与截面受压区合力作用点之间的内力臂;按有效受拉混凝土截面面积计算的配筋率ρs=As/A,ρp=Ap/A,ρcf=Acf/A,A为有效受拉混凝土截面面积,取A=0.5bh+(bf-b)hf;ds为非预应力钢筋直径,ds为预应力筋束直径,tcf为CFRP布厚度,ftk为混凝土轴心抗拉强度标准值.
考虑混凝土保护层厚度及钢筋间距对裂缝间距的影响,平均裂缝间距可表示为
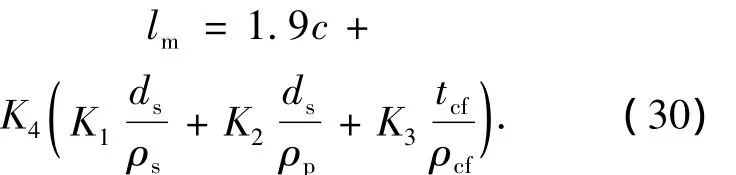
文献[11]指出,试验及理论分析表明,在使用荷载下M≈(0.6~0.8)Mu,梁处于受力的第Ⅱ阶段,截面的相对受压区高度ξ=x/h0变化很小.笔者采用数值迭代方法对CFRP布加固预应力混凝土梁进行了正截面承载力仿真分析,并得到了与文献[11]相同的结论.同时文献[6]指出,针对不同的混凝土强度、截面尺寸、加固量和配筋率进行了大量计算分析,结果表明,内力臂系数η和εcf/εs的变化范围不大,可取为常数.
可见,在受压边缘混凝土达到极限压应变之前,混凝土受压区高度y变化很小,故取正常使用极限状态的弯矩值Mk所对应的混凝土受压区高度y来计算系数χ和ζ,并认为加固梁的内力臂系数ηc,ηs,ηp,ηcf保持不变.
文献[12]考虑了箍筋的有利影响,提出钢筋与混凝土平均粘结强度τs的理论计算公式.笔者将15个拉拔试件的计算结果与试验结果进行比较,发现该公式计算结果与试验结果误差的均值为0.23,标准差为0.028.因此提出用系数ν=1.23对原式加以修正,修正后的计算公式为
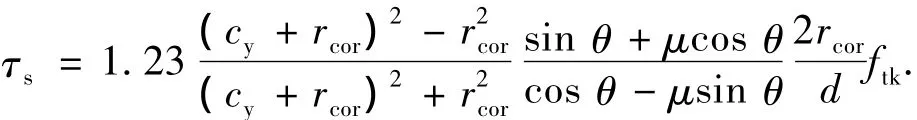
通过对文献[13]中试验数据的分析可知,φp15有粘结预应力钢绞线与混凝土的粘结强度τp较等直径变形钢筋的粘结强度τs小很多,而且因预应力孔道成型工艺、预应力钢绞线在孔道内的偏心程度、预应力钢绞线根数不同,存在较大差异.因此笔者提出,对与φp15有粘结预应力钢绞线直径相仿的直径d=16 mm变形钢筋与混凝土的粘结强度τsd16进行适当折减,来获得φp15有粘结预应力钢绞线与混凝土粘结强度τp的分析思路,其计算公式为

式中κ为折减系数,取值如表1所示.因试验数据有限,n=1,4所对应折减系数值是根据试验结果回归得到的,其它均为线性插值所得.该部分内容尚需开展更多试验工作加以完善.
对文献[8]中碳纤维布与混凝土之间的粘结强度计算公式进行整理,可得
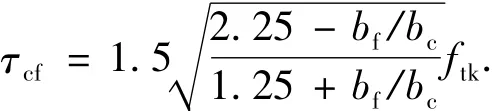
2.2 裂缝宽度
建立正常使用阶段CFRP加固预应力混凝土梁裂缝截面的弯矩平衡方程:
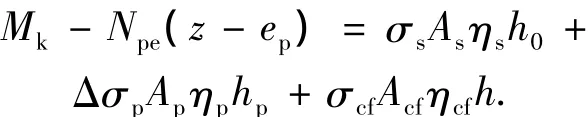
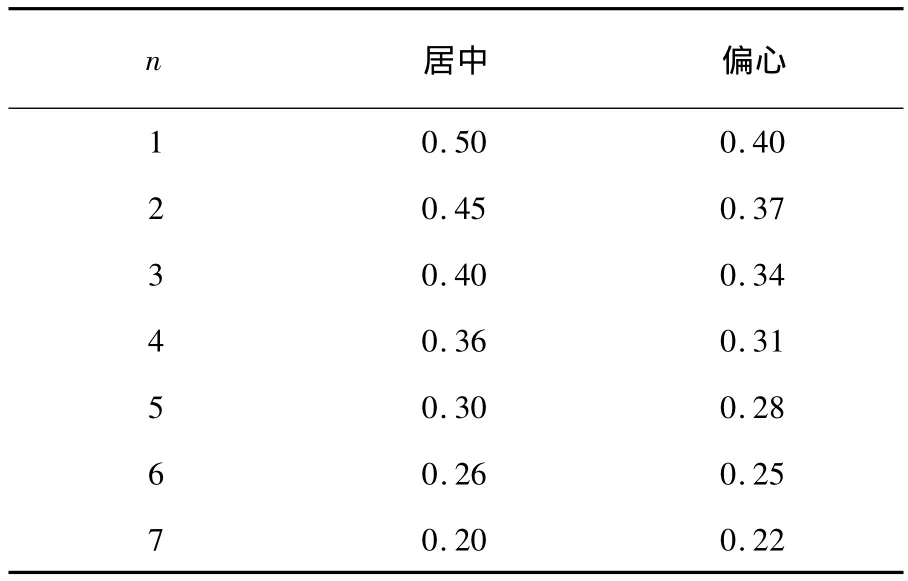
表1 折减系数
根据平截面假定可得
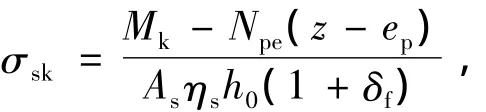
CFRP布加固预应力混凝土梁的短期平均裂缝宽度可取为平均裂缝间距范围内钢筋与混凝土平均受拉伸长之差,因此可按《规范》裂缝宽度的公式计算:
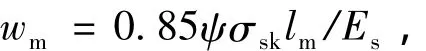
短期荷载下,最大裂缝宽度与平均裂缝宽度相比,需要引入一个裂缝扩大系数,仍沿用未加固混凝土梁的统计结果,取1.66,则
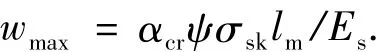
式中受弯构件αcr=1.66×0.85=1.41.考虑荷载长期作用影响时,还应引入长期作用影响系数1.5.ψ为受拉钢筋应变不均匀系数,根据其定义,可取文献[12]给出的经验公式
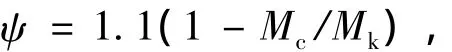
考虑到混凝土收缩对Mc的影响,取降低系数为0.8,则Mc为
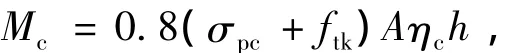
式中σpc为预加力在抗裂验算边缘产生的混凝土预压应力.
整理后得到ψ为
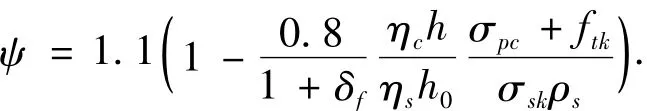
3 数据对比
在有限的数据资料中,挑选21根CFRP布加固混凝土梁的试验结果,与采用本文两种裂缝分析方法计算所得结果进行比较.裂缝间距对比结果见表2,裂缝宽度对比结果见表3.
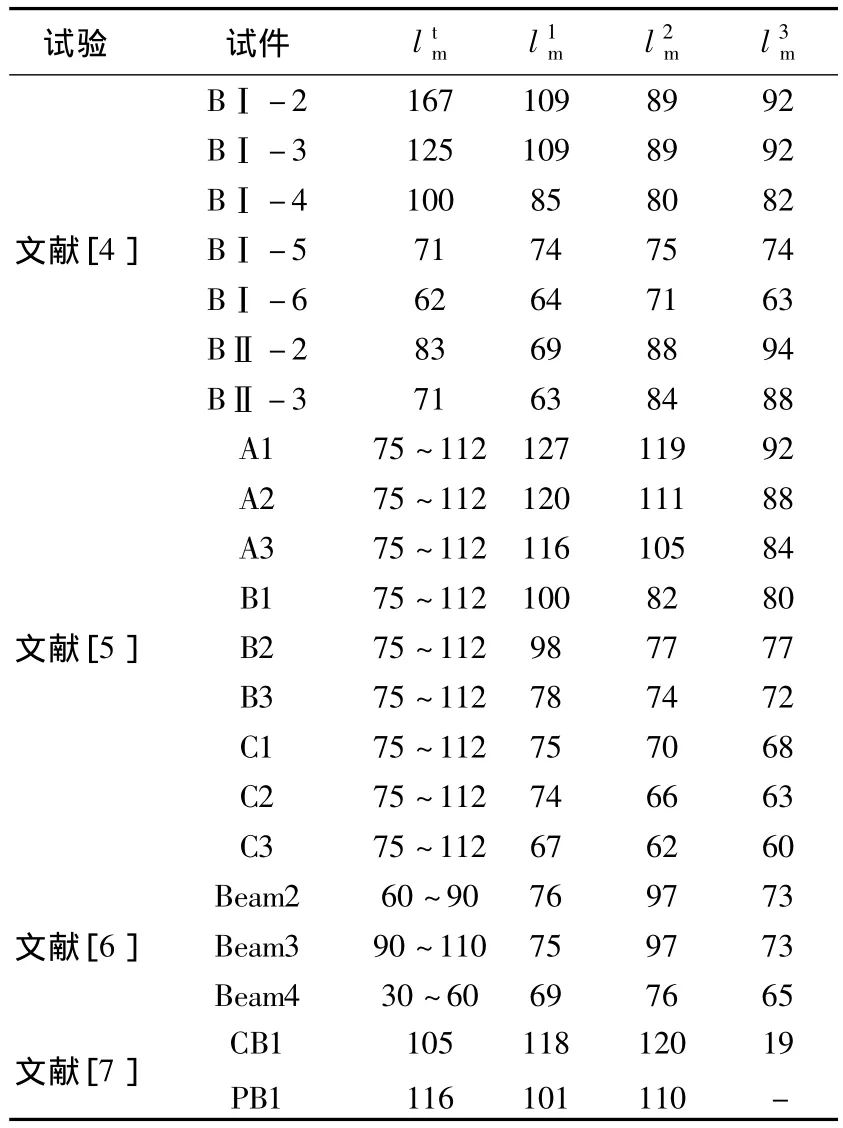
表2 裂缝间距对比mm
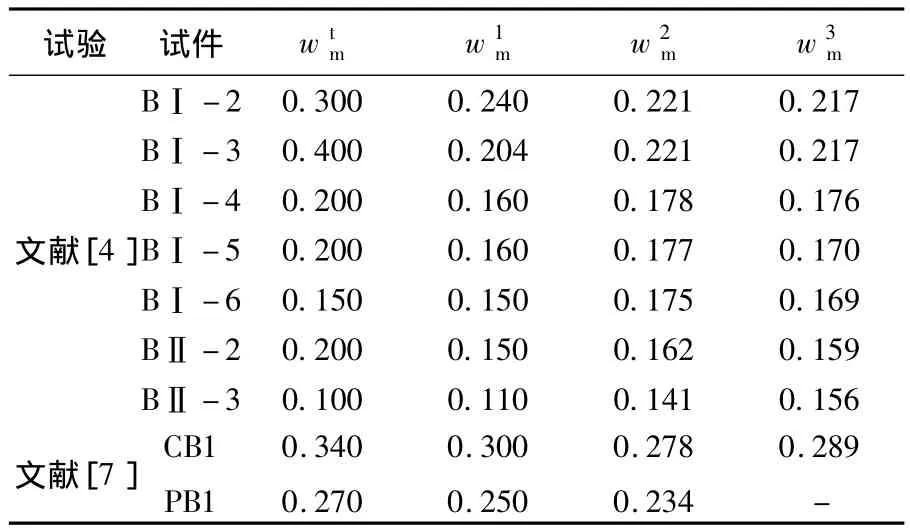
表3 裂缝宽度对比mm
由表2对比结果可知,根据本文理论分析方法和实用方法所得裂缝间距计算值与试验实测结果相差不大.经计算,按本文理论分析方法所得裂缝间距计算值与实测值之比的平均值为0.950,标准差为0.140;按本文实用方法所得裂缝间距计算值与实测值之比的平均值为0.955,标准差为0.196.
由表3对比结果可知,根据本文理论分析方法和实用方法所得裂缝宽度计算值与试验实测结果相差不大.经计算,按本文理论分析方法所得裂缝宽度计算值与实测值之比的平均值为0.841,标准差为0.144;按本文实用方法所得裂缝宽度计算值与实测值之比的平均值为0.908,标准差为0.248.
4 结语
基于粘结-滑移理论提出的CFRP布加固混凝土梁裂缝宽度理论分析方法和按照传统钢筋混凝土结构裂缝分析思路建立的实用分析方法,均较直观的反映CFRP布对裂缝开展的影响,且计算结果与试验结果吻合较好.实用计算方法计算相对简便,可用于工程设计.
[1]SHAHAWY M,CHAALAL O,BEITELMAN T E,et al.Flexural strengthening with carbon fiber-reinforced full-scale girders[J].ACI Structural Journal,2001,98(5):735-743.
[2]SMITH S T,TENG J G.Shear-bending interaction in debonding failures of FRP-plated RC beams[J].Advances in Structural Engineering,2003,6(3):183-199.
[3]SERGIO F B,SHARON L W,MICHAEL E K.Full-Scale tests of bridge components strengthened using carbon fiber-reinforced polymer composites[J].ACI Structural Journal,2003,100(6):775-785.
[4]LAURA A,ANTONIO B,GIUSY F.Increasing the flexural performance of RC beams strengthened with CFRP materials[J].Construction and Building Materials,2005,19(1):55-61.
[5]WANG Wenwei,LI Guo.Experimental study and analysis of RC beams strengthened with CFRP laminates under sustaining load[J].International Journal of Solids and Structures,2006,43(6):1372-1387.
[6]庄江波,叶列平,鲍轶洲,等.CFRP布加固混凝土梁的裂缝分析与计算[J].东南大学学报,2006,36(1):86-91.
[7]ZHENG Wenzhong,XIE Hengyan,YANG Chun feng.Analysis and calculation of factors on curvature ductility of unbonded prestressed concrete beams[J].Journal of Harbin Institute of Technology(New Series),2007,14(1):18-22.
[8]陆新征,叶列平,腾锦光,等.FRP-混凝土界面粘结滑移本构模型[J].建筑结构学报,2005,26(4):10-18.
[9]韩燕.碳纤维布加固混凝土梁变形及刚度分析[D].镇江:江苏大学,2006.
[10]王英.预应力混凝土梁板中无粘结筋应力增长规律研究及应用[D].哈尔滨:哈尔滨工业大学,2007.
[11]滕智明,朱金铨.混凝土结构及砌体结构[M].北京:中国建筑工业出版社,2005.
[12]高向玲,李杰.钢筋与混凝土粘结强度的理论计算与试验研究[J].建筑结构,2005,36(4):10-13.
[13]王英,郑文忠,卫纪德,等.预应力钢绞线(束)粘结锚固性能初探[J].工业建筑,1994(3):19-23.
- 哈尔滨工业大学学报的其它文章
- 内置钢箱-混凝土连续组合梁受力性能试验

