CJK6140数控车削物理仿真振动模型研究
张少伍,黄 杰,韩 江,钱金明
ZHANG Shao-wu1, HUANG Jie2, HAN Jiang3, QIAN Jin-ming4
(1.铜陵学院 机械工程系,铜陵 244000;2.安徽省白湖阀门厂有限公司,庐江 231508;3.合肥工业大学 机械与汽车工程学院,合肥 230009;4.华强机械股份有限公司,诸暨 311835)
0 引言
随着制造技术和信息技术的发展,虚拟制造技术实现了虚拟与现实之间的一种映射,其本质是利用计算机支持的仿真技术实现产品设计、制造的优化。虚拟加工过程仿真是虚拟制造的底层关键技术,包括数控几何仿真和物理仿真两个部分。几何仿真主要是根据数控程序,仿真工艺系统运动部件的几何运动轨迹,而物理仿真是数控仿真的核心,它是通过仿真切削过程的动力学特性来揭示加工过程的物理本质,通常物理仿真研究的内容有工件表面质量模型、切削力模型、切削振动模型、切削材料微观硬度分析模型、切削温度模型、切削加工误差模型和切削加工刀具变形模型等等。由于物理仿真切削机理复杂、建模难度大、涉及因素多等客观原因,目前的研究都还在不断的进行着。如W.J.Emdres建立了车削力的动态模型和工艺系统的振动模型,Sata等开发的刀具与工件相对振动模型,Zhang和Kapoor建立了考虑加工过程中随机振动影响的表面粗糙度模型,合肥工业大学刘光复等人提出了同时考虑工件系统和刀具系统的切削颤振模型等等,但这些模型多是对切削加工过程中的某些物理现象做定性分析,目前所做的研究还不能完全满足生产的要求,尚需作进一步的研究。本文在前人分析的基础上,对CJK6140数控车削切削振动模型进行研究,为分析刀具振动对加工工件表面质量和切削力的影响打下基础。
1 数控车削振动的形式
切削加工过程中由于各种干扰因素的存在,切削振动是无法避免的。切削中如有振动发生,不仅会降低工件的表面质量,加剧刀具磨损,破坏机床的连接特性,还会产生刺耳的噪声,严重污染环境。由于车削系统是由机床-工件-刀具构成,在车削加工中存在着各种形式的振动,按照受力类型来分,主要有受迫振动、自由振动、自激振动和混合型振动。
1.1 受迫振动
指切削加工过程中传动机构的不平衡力,断续切削的冲击力,从机床、工件、刀具中产生的脉冲性干扰而引起的振动。
1.2 自由振动
指切屑生成的周期性、断续切削产生的交变切削力,空运转时已存在的周期性激振力,刀具碰到工件材质不均的硬点产生的动态力,通过机床系统本身的弹性恢复维持的振动。
1.3 自激振动
又称颤振,是在工件和刀具之间自发产生的振荡,是由再生效应、切入效应、切削力下降特性、摩擦效应及振型关联等原因产生的交变切削力引起的振动。自激振动是由于机床—刀具—工件系统本身造成的。
1.4 混合型振动
综合了受迫振动和自激振动的变化规律。从车削振动类型分析中可看出,车削加工过程中振动形式多样,机理复杂,涉及到工艺系统的多方面因素。因此研究车削振动应从总结切削加工中的振动规律入手,重点分析切削系统的振动特点,建立适合仿真系统开发与应用的振动模型。
2 数控车削振动模型分析
在数控车削加工系统中,由于加工过程的振动既影响工件表面质量和机床的稳定性,又影响刀具的磨损,因此对振动的仿真既能预测工件表面粗糙度和刀具寿命,还能确定机床的稳定性极限。而切削力、工件材料、刀具形状、机床刚度等因素都影响机床的振动,因此对加工系统进行合理简化以建立既能反映实际情况,又便于分析车削系统振动特性和振动规律的振动模型是必要的。由于数控车削沿工件径向的振动直接影响切削深度,进而影响切削力的变化和表面粗糙度,再生效应引起的振动也主要出现在工件的径向,径向振动对表面粗糙度的影响也最大。因此本文研究切削力引起的径向振动情况,如图1所示。
根据前人的研究理论,可将径向振动的方程采用单自由度二阶模型来表达,即:
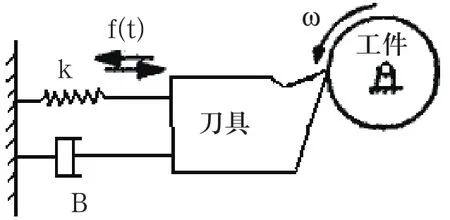
图1 车削加工振动系统简化

式中m、B、k是车削仿真模型在径向的等效质量、阻尼系数和弹簧弹性系数,f(t)为径向的切削力分量。
3 CJK6140物理仿真振动模型的实验研究
针对CJK6140物理仿真模型的数学表达式,通过实验测量振动模型在径向上的工艺系统参数,包括测量车床系统的静刚度及阻尼,由此可确定该系统的数学模型。
3.1 车床工艺系统静刚度的测量
工艺系统的刚度表征工艺系统抵抗变形的能力,一般可用力和在该力作用下的静态位移的比值来表示,即:

车削加工工艺系统是由机床、刀架、尾座、工件组成的复杂系统,刀具和工件的相对位移是组成工艺系统的各个部件位移的叠加,工艺系统的静刚度与各个部件静刚度的关系为:
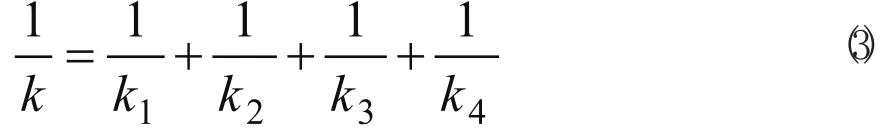
式中k1到k4分别为机床、刀架、尾座和工件的弹性系数。
由于工件材质的不均匀、材料表面的硬度差异及切削点的变化等因素,导致加工工艺系统的刚度是时变的。本文的研究将工艺系统的参数中工件部分参数单独计算,其他部分由实验确定的阻尼视为工艺系统阻尼。
按JBIT4368.4-96标准中5.5项静刚度实验之规定,采用力传感器和千分表在CJK6140车床上测得主轴部件、刀架和尾座的位移及刚度如表1所示。
依据上述公式,可得工艺系统的静刚度为:
K=9.66 N/um
3.2 车床工艺系统阻尼的测量
本文通过测量工艺系统的阻尼比来确定工艺系统的阻尼。由机械振动理论知,振动系统的各参数存在以下关系:

则工艺系统的阻尼B为:

而阻尼比ζ的测量方法有自由振动法和共振法。本文采用共振法。其原理是单自由度系统在受迫振动时,当激振频率接近系统固有频率时振动响应显著增大,根据其幅、频率响应曲线估算出振动系统的动态参数。共振法分为幅频曲线分析法、实虚部频率特性分析法和相频曲线分析法三种方法。

表1 主轴部件、刀架和尾座的刚度统计

图2 幅频曲线分析法求系统的阻尼比
幅频曲线分析法是对系统施加正弦激励信号,输出达到稳定后测量输出与输入的幅值比和相位差,逐渐改变激励信号的频率,绘制系统的频幅特性曲线。曲线幅值最大处的频率就是系统的固有频率,在固有频率的处作频率轴的平行线,相交特性曲线于a、b两点,这两点处对应的振动频率分别为ω1、ω2,如图2所示,则阻尼比ζ为:

经实验测量,系统的阻尼比ζ=0.05,B=0.783N.s/um,m=9.985kg
3.3 车削径向力的确定
在(1)式中的f(t)为激振力的径向分力,可由两种方法换算得到。一种是根据车刀的前角、刃倾角、主偏听偏角等几何角度,由各车削分力的空间关系计算出;另一种是由车削力的经验公式直接得到。本文不再讨论。
根据实验数据可得到本CJK6140数控车床径向切削振动的物理模型为:

4 结束语
虚拟仿真的目的就是在计算机内部对加工过程进行仿真,并在此基础上对加工过程进行预测和评价。本文在简要回顾数控仿真类型的基础上,分析了数控车削过程中的振动类型,建立了CJK6140数控车削过程中刀具沿工件径向单自由度振动仿真模型,并通过实验确定了工艺系统振动模型的系数,为CJK6140数控车床的振动仿真提供了理论依据。
[1] Yu Guo,Wenhe Liao,Xiaosheng Cheng,Liang Liu.SimOpt:A New simulation optimization system based virtual simulation for manufacturing system[J].Simulation Modeling Practice and Theory,2006(14):577-585.
[2] 陈秀生.基于STEP-NC的数控车削加工仿真关键技术研究[D].山东大学,2007.
[3] 黄学梅.虚拟数控车削加工物理仿真系统研究[D].东北大学,2001.
[4] 李红军.数控车削表面质量物理仿真与研究[D].南京理工大学,2005.
[5] 张少伍,韩江,胡慧萍.虚拟数控车削加工物理仿真技术研究[J].机械设计与制造,2010(3):166-168.
[6] 韩志华,罗学科.机床加工过程中的振动实验研究[J].机床与液压,2007.35(2):77-79.
[7] 陈秀生,张承瑞,刘日良,兰红波.数控加工物理仿真技术研究[J].组合机床与自动化加工技术,2006,(9):8-11.

