迫零准则下的V-BLAST检测算法比较
李婧卿,张春业,宁祥峰
(山东大学信息科学与工程学院,山东济南 250100)
作为第四代移动通信的关键技术之一,多入多出MIMO技术能够大大提高系统容量和频谱利用率,使得系统可以在不增加带宽与发射功率的情况下传输更高速率的数据。MIMO系统中的多天线能够同时提供分集增益与复用增益 ,空时编码STC技术是抗信道衰落和提高系统容量的一种最新的编码方法。现有的空时编码技术可以分为两大类[1]:空间分集技术和空间复用技术。空间分集技术目前主要有两种形式:空时网格码ST TC和空时分组码STBC。空间复用技术最典型的代表是垂直分层空时结构V-BLAST[2]。
1 MIMO简介
MIMO系统在发射端和接收端均采用多天线(或阵列天线),传输信息流经过空时编码形成M个信息子流,M个子流同时发送到信道,各发射信号占用同一频带,因而并未增加系统带宽。若各发射接收天线间的信道响应独立,则多入多出系统可以创造多个并行空间信道。通过这些并行空间信道独立地传输信息,数据率必然可以提高。MIMO信道模型如图1所示。
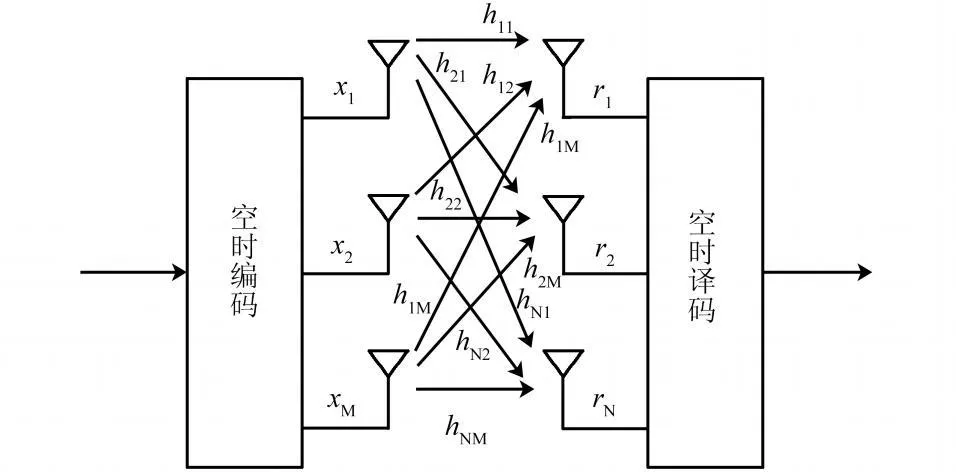
图1 MIMO信道模型
系统模型可以用矩阵表示如下:

式中,r为接收信号向量,x为发送信号向量,H为信道矩阵,n为接收端噪声向量。
2 V-BLAST编码技术
为方便起见,假设M=4,该信道编码器的输出如图2所示。每个发送符号c的上标代表信道编码器编号,下标代表发送时刻。
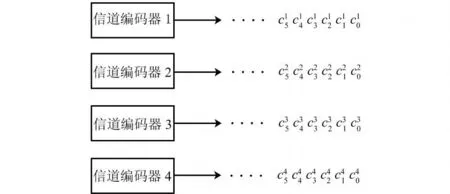
图2 信道编码器的输出
垂直分层空时编码器接收并行信道编码器的输出,然后按照垂直方向进行空间编码,其原理如图3所示。
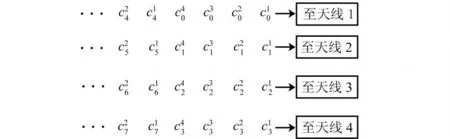
图3 垂直分层空时码的编码原理
第1个信道编码器输出的最开始的前M个码元被排在第一列,第2个信道编码器输出的最开始的前M个码元被排在第二列,而第i个信道编码器输出的第j批M个码元被排在第[i+(j-1)·M]列。编码后的空时码元矩阵中的每一列,分别经M个发送天线同时发射。
3 四种V-BLAST系统的检测算法比较
3.1 ZF检测算法
迫零ZF(Zero Forcing)算法只是简单的利用信道矩阵H的伪逆H+作为线性组合器,在式(1)两端左乘H+,然后再对结果量化得到的x估计值。
3.2 ZF-OSIC检测算法
(1)不排序加干扰抵消的迫零ZF-SIC算法
在研究译码算法的过程中,Foschini等人提出了一种连续干扰删除SIC(Successive Interference Cancellation)技术[3],通过用一个迫零向量对接收信号向量加权来去掉干扰。在每一个检测步骤中,除了需要检测出目标信号外,其它信号都被认为是干扰。通过使用迫零向量来删除这些信号干扰,目标信号就可被检测出来,然后从接收信号中去除干扰。
迫零的检测方法就是找到一个加权矩阵W,使其满足以下的关系

其中,Wi和Hj分别表示加权矩阵W的第i行和信道矩阵H的第j列。满足这个条件的加权矩阵就是信道矩阵H的伪逆矩阵,即W=H+=(HHH)-1HH。检测时,假设先检测信号 x1(即发送信号向量的第一个元素),用加权向量w1对接收信号进行加权并量化判决得到x1的估计值 x1。然后把信号x1产生的干扰从接收信号向量r1中减去,得到修正后的接收向量r2=r1- x1H1。把去掉信道矩阵第1列的矩阵的伪逆作为下一个加权矩阵继续检测下一个信号,进而依次检测出所有码字。
不排序的ZF-SIC译码算法中,发送信号的检测顺序是任意的,但是发送信号的检测顺序对系统的译码性能有很大影响,所以检测时排序可以提高系统性能。
(2)排序加干扰抵消的迫零ZF-OSIC算法
信号检测后的信噪比为
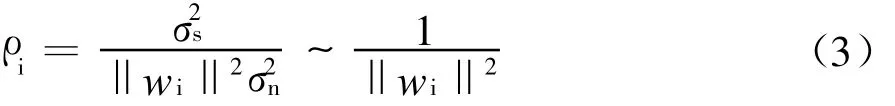
3.3 QR分解检测算法
矩阵的QR分解是在信号处理中应用最广泛的一种矩阵分解,它是将矩阵分解为一个酉矩阵和一个上三角矩阵的乘积。QR分解算法[4]一方面简化了线性迫零的运算,另一方面也增强了算法的稳定性。
这种检测算法的主要思想是,对信道矩阵H进行QR分解,一个N×M的酉矩阵Q,一个M×N的上三角矩阵R。接收信号向量r乘以QT得到y=QTr,进而y=Rx+QTn。y的第i个分量只取决于第i层以及更高层的传输符号。检测时,首先检测最底层的信号xM,因为它只和RM,M有关,然后自底向上逐层检测,经量化判决后得到各码字的估计值。
3.4 SQRD检测算法[5]
排序的QR算法SQRD应用了修正的Gram-Schmidt方法,从左至右逐列求解矩阵Q,从上至下逐行求解矩阵R。具体过程为:对于给定的信道特性矩阵H=[h1,h2,…,hM],首先对M个列向量分别求范数,将范数最小的一列记为第k1列,然后将矩阵的第1列与第k1列互换位置,即h1=hk1,则矩阵R的第一个对角线元素为R1,1=‖h1‖,而矩阵Q的第1列q1=h1/R1,1,矩阵R的第一行其余元素为=(2≤i≤M)同时矩阵H的其余各列将变为=hi-q1R1,i(2≤i≤M)。对于由列向量,.…,构成的矩阵重复执行以上过程,即可求得矩阵Q和矩阵R。接下来的信号检测部分和QR分解算法一样,都是按自底向上的顺序逐步进行。
3.5 算法复杂度定量分析
上述的四种检测算法的复杂度比较如下。
(1)由于ZF算法就是直接对信道矩阵H求伪逆的过程,显然它是一种最简单的算法,复杂度最低。
(2)在ZF-OSIC算法中,需进行次M对矩阵求伪逆的运算和M次排序运算,求矩阵伪逆的计算量大约占到整个计算量的80%。可以证明,当发射天线数和接收天线数相等(M=N)时,原始的 VBLAST检测算法中计算伪逆矩阵部分的计算复杂度与27M4/4成正比。当发射天线个数较多时,算法的计算复杂度非常高。
(3)基于QR分解的算法采用了串行干扰抵消的思想,从底层开始逐层检测,循环次数与发射天线数M相等。显然,对信道矩阵H进行QR分解可以显著降低迫零算法的复杂度,当发射天线数和接收天线数相等时(M=N),QR分解的计算复杂度与8M3/3成正比。
(4)为了达到与ZF-OSIC一致的性能,需要对QR分解算法进行排序,使每一步检测的信噪比最大。可以证明,最优的排序可以通过比较M2/2次QR分解而得到,但这样计算复杂度非常高。SQRD算法可以减小计算量,该算法既可实现最优检测顺序,使系统性能达到与ZF-OSIC可比拟的程度,又大大减小了计算复杂度,是一种比较折衷的算法。
4 仿真结果及分析
4.1 仿真平台及参数设置
使用Matlab仿真平台,仿真参数设置如下:发射信号为[0,1]序列,采用未编码的BPSK调制,每一帧信号总功率Es=1,发射功率在各天线上平均分配。假设信道为瑞利慢衰落信道,信道矩阵元素的实部和虚部是独立同分布零均值复高斯随机变量,每个方差为1/2。接收端噪声为加性高斯白噪声,噪声功率为N0/2。并假设接收端实现了精确的同步并正确估计信道系数,定义每个接收天线上的比特信号噪声比为Eb/N0。
4.2 仿真结果及性能分析
仿真过程中,采用ZF、ZF-OSIC、QR和 SQRD四种检测方法对系统进行Monte Carlo仿真,令比特信号噪声比在[0,24]dB区间取值,每隔2dB运行一次程序,得到对应的误比特率 BER,最后以Eb/N0的值为横坐标绘出误比率BER曲线,如图4~6所示。
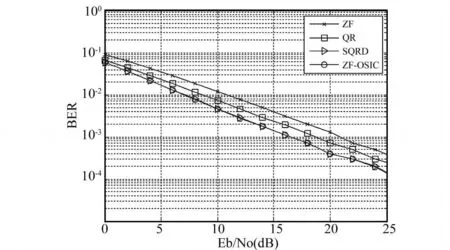
图4 四种算法下系统误码率曲线(M=N=2)
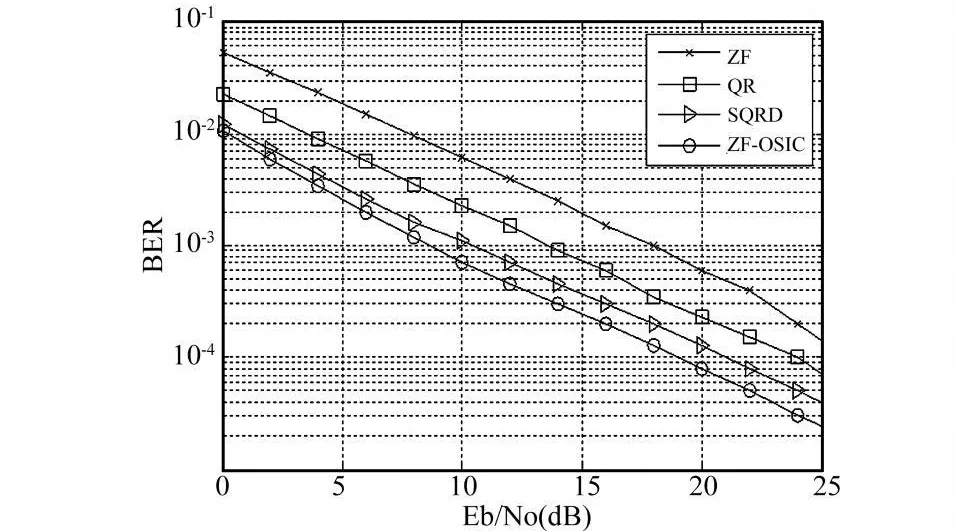
图5 四种算法下系统误码率曲线(M=N=4)
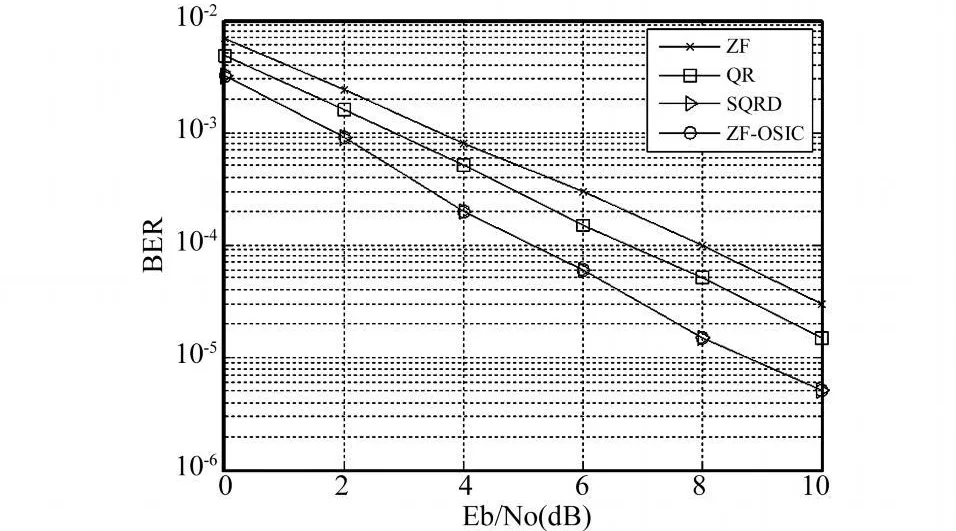
图6 四种算法下系统误码率曲线(M=2,N=4)
由图4可以看出,当系统2发2收时,不进行干扰抵消的线性ZF检测的性能最差,这是因为它在对信道矩阵求伪逆的过程中同时对噪声的干扰进行了放大。其次是未排序的QR分解算法,由于它引入了干扰抵消的过程使得误码率性能比ZF算法有约2dB的提高。SQRD算法和ZF-OSIC算法比前两者的接收性能又有所提高,这是排序的过程带来的好处。经过排序,系统按照信噪比从大到小的顺序进行检测,降低了误码率。可是,由于天线数太少(仅有两根天线),所以排序的优点表现得不十分明显。另外我们可以看到,SQRD算法和ZF-OSIC算法在性能上取得了不相上下的结果,然而前者的计算复杂度却比后者小得多。
天线数量增加到4发4收以后,系统的复用增益由2增加到4。由图5可以看到,四种检测算法下的系统性能与2发2收系统相比也分别有了一定的提高。而且SQRD与ZF-OSIC这两种算法相对于ZF和QR算法而言,对检测性能提高的程度也有所改善,我们可以很清楚的看到排序带来的好处。同时SQRD算法与ZF-OSIC算法相比,出现了约ldB的性能损失。可是ZF-OSIC算法的计算量是四种算法中最大的,它以巨大的计算复杂度换取了系统性能的提高。所以,在实际应用中,我们选取计算量不是很大而系统性能又比较可观的SQRD算法是一种较合理的选择。
图6给出了发射(M=2)和接收(N=4)天线数不同时系统的接收检测性能。可以看到,当接收天线数大于发射天线数时,系统性能得到进一步提高。在仿真条件均相同的条件下,与2发2收系统相比接收性能改善了至少10dB以上。在接收端信噪比为10dB时,即使采用检测性能最差的ZF算法,误码率也可达到10-5数量级,这是分集增益的体现。由于接收端天线数比发射端多2,相当于每个发射信号多了两路接收,使衰落的可能性减少,误码率自然会降低。
5 结语
四种检测算法中,在其他条件均相同的前提下,接收端采用ZF-OSIC算法时系统的误码率最低,性能最好。采用SQRD算法的系统性能与ZF-OSIC的相差不大而复杂度更低,是一种比较折衷的检测方法。在检测过程中引入干扰抵消的思想以及排序过程对提高系统性能都有一定的帮助。
最后,由于本文仅对基于迫零准则的四种检测算法进行了研究,所以得到的结论并非具有代表性,此后将对基于最小均方误差准则的各种算法进行进一步研究。
[1] 王晓海译.空时编码技术[M].北京:机械工业出版社,2004:23-24
[2] Foschini G.Layered space-time architecture for wireless communication in a fading environment using multi-element antennas[J].Bell Labs Technical Journal,1996,1(2):41-59
[3] Wolniansky P.W,Foschini G.J,Golden G.D,Valenzuela R.A.V-BLAST:An A rchitecture for Realizing Very High Data Rates Over the Rich-Scattering Wireless Channel[J].Signals Systems and Electronics,1998,3(12):295-300
[4] 刘海涛,孙宇昊,李冬霞.基于 QR分解的循环迭代检测算法[J].新乡:电波科学学报,2005,20(5):575-579
[5] Wubben D.Efficient algorithm for decoding layered space-time codes[J].IEEE Electronic Letters,2001,37(22):1348-1350

