光伏电池运行失配模式及特性分析①

宋 菁，徐青山，祁建华，周 琦

(1.东南大学电气工程学院，南京 210096;2.宁波市象山县供电局，宁波 315700)

在太阳能光伏发电中，光伏电池通常需要将多个模块串、并联以满足用户对电流或功率的要求。但光伏电池作为太阳能光伏发电系统的基本发电单元，容易受到周围建筑物、树木和电线杆以及天空中乌云等阴影的影响。当串、并联电池模组中出现上述阴影现象，就可能导致模组特性变坏，能量输出能力降低，甚至形成热岛效应，损坏模组。有关太阳能失配方面已经有较多学者做了一定的研究[1～4]，但是大部分研究都是基于模块在单一运行方式下的仿真讨论。因此，本文对太阳能模组串、并联不同失配模式下的运行特性及补偿措施作了进一步的研究。

1 太阳能电池模型

常见的太阳能模型如下图1[5]所示。

图1 太阳能电池等效示意图Fig.1 Sketch of equivalent circuit of solar cell

从图1可以看出，在外接负载的情况下，存在着以下关系:

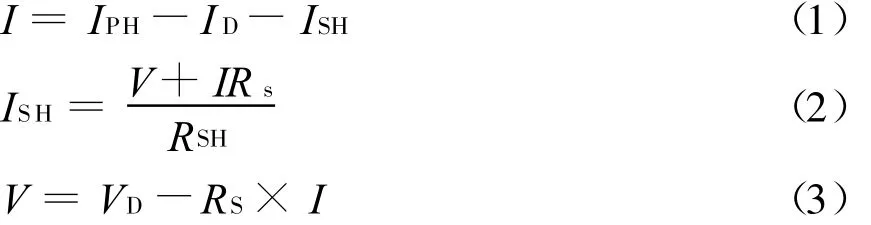
二极管电流可以表示为

式中:q为电子的电荷量，1.6×10-19C;k是波尔兹曼常数，1.38×10-23J/K，T为环境温度，要转换成绝对温标;n为二极管的理想因数，通常取为1.3左右。

Iph为太阳能电池的光生电流，近似等于太阳能电池的短路电流Isc:

以日本京瓷株式会社生产的SPG1786型太阳能模组为例。SPG1786型模组共计具有48个太阳能电池，其最大输出功率为178.6W。根据厂家提供的数据，标准测试条件STC(standard testing conditions)下，即电池温度设为25℃，辐射强度设置为1000 W/m2，SPG1786型模组的特性曲线如图2[6]所示。

图2 SPG1786模组特性曲线Fig.2 Behavior curve of SPG1786 module

2 太阳能电板串联特性研究

2.1 不同辐射两模块串联运行特性

研究场景作如下假设:2个SPG1786直接串联，辐射强度分别为 1000 W/m2、800 W/m2。仿真得到特性曲线如图3所示。

2.2 串联失配补偿策略及算法描述

当太阳能模板直接串联时，根据电路要求，辐射强度低的模块因为电流较小从而限制了整个电路的电流。为了弥补这一损失，可以通过添加旁路二极管以导通剩余电流来提高电路的性能及其输出功率[7，8]。改进模型如图4所示。

图3 两个不同辐射的SPG1786串联运行特性Fig.3 Curves of two SPG1786 in series at different irradiation level

图4 添加旁路二极管后串联电流的模型Fig.4 Equivalent circuit for series connection

图4中的旁路二极管作用在某个串联模块受到阴影的情况下。此时，与受阴影影响的模块并联的二极管适时正向导通流过补偿电流，提供一个能量散逸的途径，虽然二极管的添加造成了一定的能量，但电路的电流运行范围扩大了，整个电路的运行性能也得到较大的改善。

如图4，如果以Ns表示该太阳能模组总电池数，假设有m个旁路二极管，则每个旁路段包含Ns/m个太阳能电池。即可得:

整个模组的输出总电流可以分为2个部分:第1部分是太阳能电池回路部分所流通的电流;第2部分便是旁路二极管支路所流通的电流。如果以I1+Id1表示总串联电流的话，则对于m个旁路区段可以列出m-1个独立方程，即

每1个区段的太阳能电池串联电阻和并联电阻是该模组总串联电阻和并联电阻阻值的1/m。一共可以列出m个独立的区段太阳能电池方程，即

这样，对于m个旁路区段的太阳能电池流通电流和m个旁路电压(即区段太阳能电池输出电压)共2m个变量，可以列出2m个独立方程。由于太阳能电池I-U方程是非线性方程，因此方程组的求解可以考虑用牛顿-拉夫逊法迭代求解。

牛顿-拉夫逊法迭代格式如式(10)所示，式中Jk是雅可比矩阵。

2.3 改进后的电路运行特性

根据上面提出的补偿策略，两个SPG1786模块各并联一个旁路二极管，仿真结果如图5所示。

图5 附有旁路二极管的SPG1786串联运行特性Fig.5 Curves of two SPG1786 in series with bypass diode

2.4 对比分析

首先，从仿真得出的数据(如表1)对比可以看出，改进后的电路电流、电压、功率的范围均有所增大，其中影响较大的是电流的取值范围。另外，通过数据可以看出，改进后的电路曲线的极值点的出现有所延迟。

表1 两种电路运行特性比较Tab.1 Comparisons between two configurations

其次，从特性曲线自身走向可以发现改进后电路的功率/电压、电流/电压曲线都是双峰曲线。两个陡坡的形成是由于两种辐射强度的存在导致不同区段的太阳能电池能够提供的光生电流大小不同，从而导致了V-I曲线的扭曲，受阴影影响的区段在系统输出电流超过其能提供的短路电流大小后被旁路二极管保护，电压被钳制在负的很小电压范围内。同样原因，P-U曲线出现了双峰的现象，而且随着受阴影影响区段的辐射强度的逐步提高，第一个功率峰值越来越大。

3 太阳能电板并联特性研究

为了获取较高的电流，满足部分大功率用户的要求，太阳能电池组通常需要采用并联运行的方式。

3.1 不同辐射两模块并联运行特性

本文将并联运行电路简化为:两个SPG1786辐射强度分别为1000 W/m2，800 W/m2直接并联运行，仿真结果如图6所示。

图6 两个不同辐射的SPG1786并联运行特性曲线Fig.6 Curves of two SPG1786 in parallel connection at different irradiation levels

从图6可以看出，两个SPG1786并联运行特性曲线是单峰曲线。电路电压最大值为23 V，当电路电压超过23 V时，电压高的支路会向电压低的支路倒送电流，形成环流，电路性能大大降低。

3.2 并联失配补偿策略

当两个SPG1786直接并联运行时，由于太阳辐射不一致，电池板的电流以及温度均会出现差异，从而导致两块模组的电压不同。根据并联电路电压一致的特性，辐射正常的模块便会受到有阴影模块的影响[9，10]。此时，阻断二极管的添加可以很有效地解决这一问题。串联阻断二极管后的电路图如图7所示。

图7 阻断二极管添加后的并联电路图Fig.7 Equivalent circuit for parallel connection with string diode

阻断二极管在电压高于受阴影模块的最大输出电压时发挥作用，它给受阴影的模块提供一个电压补偿作用，使两并联支路的电压得到匹配，从而防止电压倒流，电流环流现象的产生。

3.3 改进后的电路运行特性

根据上述补偿策略，给两块SPG1786串联阻断二极管后得到特性曲线如图8所示。

图8 两个SPG1786串联阻断二极管仿真曲线Fig.8 Curves of two SPG1786 in series with stingdiode

从图8可以看出，功率/电压、电流/电压曲线都有个拐点。拐点出现在电压为23 V左右，拐点意味着在电压为23 V时，与受阴影的电池串联的阻断二极管开始起作用，提供为了匹配正常辐射情况下的电池模块的电压所需值。

3.4 对比分析

首先，从得出的数据(如表2)分析可知:阻断二极管的添加使得电路的电流、电压的取值范围均有所扩大，但两种电路的极值点是相同的。

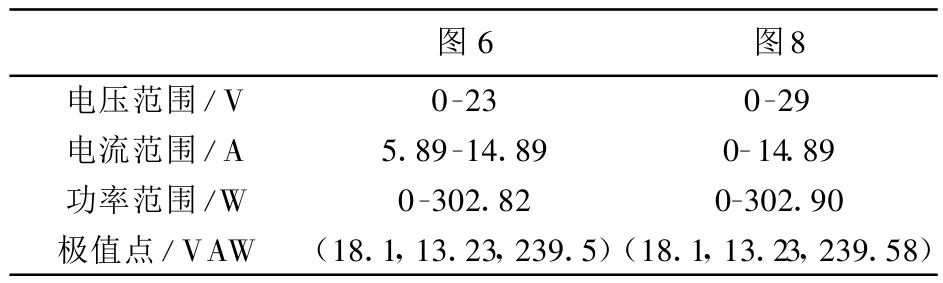
表2 两种电路运行特性比较Tab.2 Comparisons between two configurations

其次，从图7、8对比分析可知，阻断二极管只会在某个特定区域发挥它的作用(如图9中的a、b之间)。当电压小于a点电压时，旁路二极管的添加并没有太大的作用;而在区间a、b之间，当电压达到一定的数值时，如果没有阻断二极管的存在，电压高的会向电压低的倒送电流，电路便会出现故障，影响电路的性能。而如果添加了阻断二极管，阻断二极管就可以提供受阴影支路所供不足的电压，满足电路的需要，从而电路继续正常运行，提高了整个电路的性能。

图9 SPG1786在不同辐射下的特性曲线Fig.9 V-I，P-I curve of SPG1786 at different irradiation levels

4 结论

本文建立了不同辐射状况下太阳能模组的串、并联运行的电路模型，探讨出各种连接方式下的电路特性曲线，并进一步探讨失配情况下旁路二极管与阻断二极管的添加问题，最后对比得出以下结论[11，12]。

1)不同辐射的两块太阳能电池模块串联运行会因为其中某块模组短路电流较小而迫使整个电路的电流降低，进而使得两块模组的功效不能最大化，造成一定的能量损失。

2)在串联太阳能电池模组的两端并联旁路二极管可以适时正向导通流过补偿电流，提供一个能量散逸的途径，改善电流失配的状况。仿真结果表明旁路二极管的添加不仅充分扩大了电流的取值范围，同时极大地提高了串联模组的性能，降低失配带来的能量损失。

3)不同辐射的两块太阳能电池模块并联运行会因为两条支路的电压不匹配从而造成电压高的支路会向电压低的支路倒送电流，形成环流，电路性能大大降低。

4)太阳能模组并联运行时，阻断二极管在电压高于受阴影模块的最大输出电压时发挥作用，它给受阴影模块提供一个电压补偿作用，使两并联支路的电压得到匹配，从而防止电压倒流，电流环流现象的产生。

[1] Volker Q，Rolf H.Numerical simulation of currentvoltage characteristics of photovoltaic systems with shaded solar cells[J].Solar Energy，1996，56(6):8-12.

[2] Karatepe Engin，Boztepe Mutlu，Colak Metin.Development of a suitable model for characterizing photovoltaic arrays with shaded solar cells[J].Solar Energy，2007，81(8):977-992.

[3] Alonso-Garcia M C，Ruiz J M，Herrmann W.Computer simulation of shading effects in photovoltaic arrays[J].Renewable Energy，2006，31(12):1986-1993.

[4] 程军照，李澍森，张腾飞(Cheng Junzhao，Li Shusen，Zhang Tengfei).多路并网光伏发电系统的仿真与分析(Simulations and analysis on a multi-branch grid-connected photovoltaic system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA)，2009，21(4):58-62.

[5] 徐鹏威，段善旭，刘飞，等(Xu Pengwei，Duan Shanxu，Liu Fei，et al).几种光伏系统 MPPT方法的分析比较及改进(Analysis，comparison and improvement of several MPPT methods for PV system)[J].电力电子技术(Power Electronics)，2007，41(5):3-5.

[6] Sharma A K，Dwivedi R，Srivastava S K.Performance analysis of a solar array under shadow condition[J].IEE proceedings，Part G:Circuits，Devices and Systems，1991，138(3):301-306.

[7] 徐青山，卞海红，高山，等(Xu Qingshan，Bian Haihong，Gao Shan，et al).计及旁路二极管效应的太阳能模组性能评估(Performance evaluation of photovoltaic module with bypass diode effect)[J].中国电机工程学报(Proceedings of the CSEE)，2009，29(8):103-108.

[8] Chamberlin Charies E，Lehman Peter，Zoellick James，et al.Effects of mismatch losses in photovoltaic array[J].Solar Energy，1995，54(3):165-171.

[9] Roman E，Martinez V，Jimeno J C，et al.Experimental results of controlled PV module for building integrated PV systems[J].Solar Energy，2008，82(5):471-480.

[10] Karatepe Engin，Hiyama Takashi，Boztepe M utlu，et al.Voltage based power compensation system for photovoltaic generation system under partially shaded isolation conditions[J].Energy Conversion and Management，2008 ，49(8):2307-2316.

[11] Petrone G，Spagnuolo G，Vitelli M.Analytical model of mismatched photovoltaic fields by means of Lambert W-function[J].Solar Energy Materials and Solar Cells，2007 ，91(18):1652-1657.

[12] Kawamura Hajime，Naka Kazuhito，Yonekura norihiro，et al.Simulation of I-V characteristics of a PV module with shaded PV cells[J].Solar Energy Materials and Solar Cells，2003，75(3-4):613-621.