自抗扰技术在PWM整流器中的应用
赵俊梅 任一峰
(中北大学信息与通信工程学院,太原 030051)
1 引言
三相电压型 PWM整流器因其具有网侧电流正弦化、运行于单位功率因数、能量双向传输等优点,被广泛应用于无功补偿、有源滤波器、交流传动、高压直流输电及新能源的利用等领域。在PWM整流器的众多控制算法中,直接功率控制采用瞬时功率控制,具有高功率因数、网侧电流低谐波、算法及系统结构简单等优点,因其人们的广泛关注。但负载变化或存在扰动时,会引起直流侧电压的波动,传统的PI控制很难有效抑制电压的波动。
中科院系统所韩京清研究院提出了一种对不确定系统有效实用的控制器——自抗扰控制器。它将系统的参数的变化归结为系统的内扰和外扰一起形成总扰动。通过观测补偿的办法解决,具有很强的鲁棒性。其中扩张状态器可以对系统的总扰动进行观测,它不必区分扰动的形式,对非线性、耦合等复杂形式的扰动也可很好地观测。
本文将自抗扰控制技术应用在直接功率控制的PWM整流器中,采用ADRC进行电压外环控制,通过扩张状态器对负载的变化及时准确地估计和补偿,从而有效抑制负载变化带来的影响。
2 PWM整流器的直接功率控制
整流器的直接功率控制系统是建立在瞬时值基础上的三相电路瞬时无功功率理论。通过直接控制瞬时有功功率和无功功率,实现高功率因数、低谐波的控制。
整流器的直接功率控制系统结构如图1所示,根据检测到的电流 ia,ib,ic和电压 ua,ub,uc,经计算得到瞬时有功功率和无功功率的估算值p和q,与功率的给定值pref和qref比较后送入滞环比较器输出sp和sq开关信号,pref由直流电压外环设定,qref设定为0,以实现单位功率因数。三相电压 ua,ub,uc经3/2得到两相静止坐标系中的电压uα和uβ,uα和uβ送入扇形比较器输出θn信号。根据sp、sq和θn在开关表中选择所需的sp、sq和sc去驱动主电路开关。
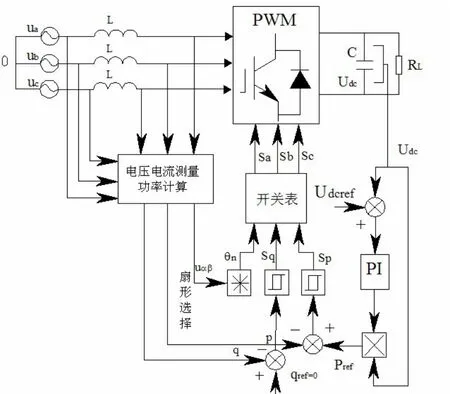
图1 整流器直接功率控制系统结构图
整流器的直接功率控制系统结构简单,控制算法容易实现,可以实现对有功功率和无功功率的精确控制。其缺点是要求较高的采样频率且开关频率不固定,造成网侧电流谐波含量随机分布,给网侧电流滤波带来困难。另外当直流侧负载发生变化时,会造成直流侧电压波动。
3 PWM整流器的自抗扰控制器的设计
3.1 自抗扰控制器原理
自抗扰控制器的典型结构包括3部分:扩张状态观测器、微分跟踪器和非线性状态误差反馈控制率。微分跟踪器 TD的作用是安排过渡过程并给出此过程的微分信号。扩张状态观测器是自抗扰控制器的核心,扩张状态观测器ESO对状态变量的估计z1(t)、z2(t) 及 系统总扰动的实时作用量的估 计z3(t) ,而反馈量 z3(t)/b0将起到补偿这个“总扰动”的作用。b0为b的估计值。非线性组合NLSEF实现对各阶误差信号的非线性加工组合。典型二阶自抗扰控制器结构如图2虚线部分。

图2 自抗扰控制器原理图
许多实际被控对象的数学模型可以简化为
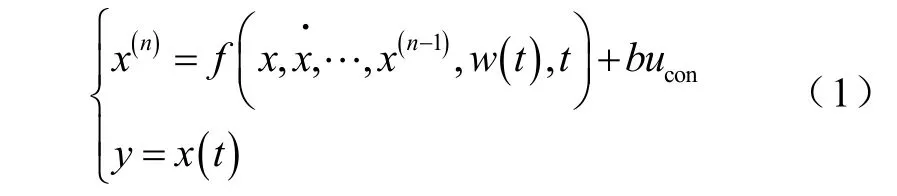
式中,w(t)为系统总扰动,它包括系统外扰和模型变化引起的内扰;x为状态,y为输出;uCON为控制量;b为系数。通过采用ESO对总扰动进行观测并给予补偿,使系统变成积分串联型系统,有
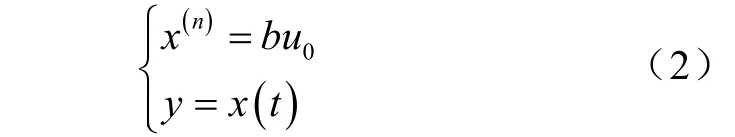
3.2 VO-DPC电压自抗扰控制器设计
一般情况下自抗扰控制器采用非线性函数设计,能够取得很好的控制效果,但计算复杂,并给调试增加了难度,所以采用线性函数来设计线性自抗扰控制器。
(1)跟踪微分器的设计

式中,r为可调参数,r越大,跟踪速度越快;udc1为安排的过渡过程;udc2为udc1的广义导数。
(2)扩张状态观测器的设计
对 PWM整流器实际直流输出电压设计的二阶线性ESO为

式中,udc为直流侧输出电压;z1为电压的状态估计;z2为扰动 a(t)的估计值; β01、β02为两个可调参数。
ESO对扰动的估计准确与否直接影响ADRC的控制效果,故ESO的参数整定非常关键,z2给出对未知扰动 a(t)的估计,影响系统的动态性能和精度,而z1的值对系统的输出也有较大影响,因为PWM整流器的输出电压存在噪声,z1起到对实际电压进行准确状态估计的作用。
(3)线性组合的设计
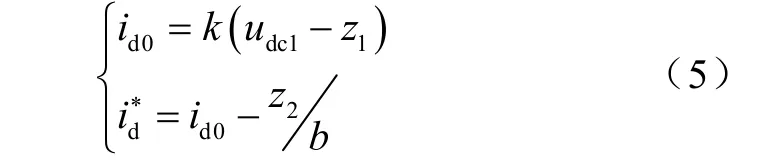
线性反馈结合ESO对耦合部分的观测,就可以将直流电压方程化为积分器串联型的线性结构,这样便完成了直流电压的自抗扰控制器的设计,设计的自抗扰控制器如图3所示。
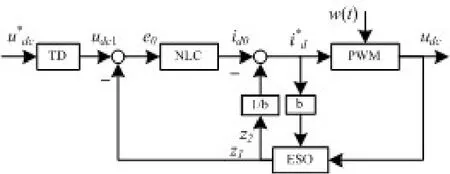
图3 ADRC控制器结构
4 仿真结果
根据整流器PI控制的直接功率控制和基于自抗扰的直接功率的基本原理,在Simulink环境下搭建其仿真模型,仿真参数设置如下:交流侧电压为110V,频率为50Hz,电感为0.028mH,电阻为0.1Ω,直流侧滤波电容为100uF,负载阻值为100Ω,直流电压参考电压输入设定为300V。仿真结果如图4所示。
图4为直流电压输出波形,输出电压快速,无超调的到达稳定状态,且稳态误差很小。
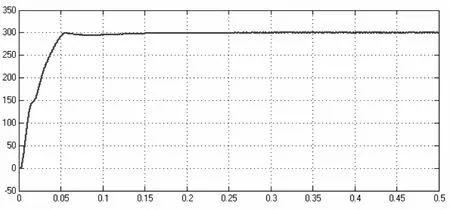
图4 直流电压输出
图5为交流侧相电压和电流波形,电压和电流的波形重合,实现了单位功率因数运行。
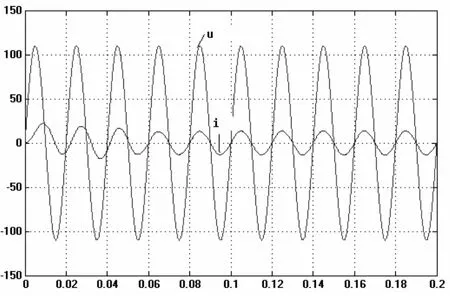
图5 交流侧电压电流输出波形
为了验证所提方案的性能,笔者经PI控制的直接功率控制和自抗扰的直接功率控制作了对比实验。其中图6为参考电压改变时输出电压的波形,在0.2s时,直流参考电压改为400V,由图6可见,ADRC控制比PI控制能更快地达到稳态。
为了验证系统对负载的鲁棒性,将系统的负载电阻在t=0.4s时由100Ω变为50Ω。图7为直流电压输出波形,由图7可见,文中所提方案具有更小的转速降和更快的恢复时间。

图6 参考电压改变时直流电压输出
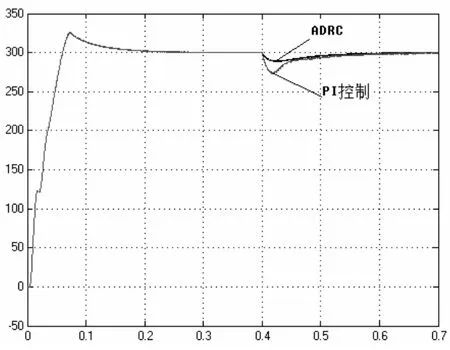
图7 负载改变时直流电压输出
5 结论
作者针对电压定向的直接功率控制的 PWM整流器,提出了一种基于自抗扰控制的电压控制方案。仿真结果表明,该方法具有单位功率因数,低谐波、动态性能好等优点,而且验证了系统对负载的扰动有明显的抑制效果。
[1]Silva N,Martins A.Design and evaluation of a PWM rectifier control system for testing renewable DC sources connected to the grid[C] Processdings of 2006 International Svmposium on Power Electronics,Electrical Drives. Automation and Motion. Piscataway, NJ,USA: IEEE,2006:32-37.
[2]韩京清.自抗扰控制其及其应用[J].控制与决策,1998,13(1): 19-23.
[3]邵立伟,廖晓钟,张宇河等.自抗扰控制器在永磁同步电机中的应用[J].北京理工大学学报,2006,26(4): 326-329.
[4]薛鹏骞,王久和,薛伟宁.电压型 PWM整流器直接功率控制系统设计[J].辽宁工程技术大学学报.2006,5:724-726.

