在ARM处理器上设计FIR低通滤波器*

何华光,陈妮,赵进创

(广西大学 计算机与电子信息学院,南宁530004)

何华光(工程师),研究方向为嵌入式系统应用;陈妮(硕士研究生),研究方向为计算机通信与信息系统;赵进创(教授),主要研究方向为成像技术、嵌入式系统应用等。

引 言

电阻抗成像技术是利用生物组织与器官的电特性及其变化,提取与人体生理、病理状况相关的生物医学信息的一种无损伤检测技术,是当今生物医学工程研究的热点课题之一[1]。电阻抗成像硬件系统中,滤波器是重要的组成部分。随着数字信号处理技术的发展,数字滤波器与传统的模拟滤波器相比具有如下优点:具有高精度和真正的线性相位响应;性能稳定,不受电压漂移、温度改变的影响;数字滤波后的数据可以存储起来以备将来观测与分析;滤波器参数的改变一般不需要改动硬件电路,降低了硬件设计的风险。因此,数字滤波器非常适合应用在电阻抗成像硬件系统中。

目前,数字滤波器主要是基于DSP和FPGA来实现的,可以实现非常高速的数字滤波器。但是,这种实现方式增加了整个电阻抗成像硬件系统的硬件开销,成本较高,而ARM处理器成本低、性能高。本文提出了基于ARM处理器的FIR低通滤波器方案,具有成本低、功耗低、开发周期短等特点,并且可以在实现数字滤波的同时发挥ARM处理器强大的控制功能,完成系统中其他的控制任务。

1 FIR数字滤波器原理

电阻抗成像硬件系统广泛使用具有线性相位的FIR滤波器,FIR滤波器的输入、输出可用下式描述:

式(1)中,h(k)(k=0,1,…,N-1)为滤波器的冲击响应系数;H(z)是滤波器的传递函数;N是滤波器长度,即滤波器系数的数目;x(k)是第k时刻的输入样本值。式(2)是FIR滤波器的时域差分方程。可以看出,FIR滤波器由乘累加器构成。其设计方法主要有窗函数法、频率抽样法和最佳方法[2]。

2 基于最佳方法的FIR滤波器设计

2.1 最佳方法设计滤波器的基本流程

FIR数字滤波器设计的主要问题是,对期望的滤波器或理想频率响应做逼近。最佳方法是指,基于切比雪夫逼近理论和最佳一致逼近法所提出的一种计算机辅助设计方法。这种方法可以获得性能优良的滤波器阻带和通带特性,并且在相同技术指标条件下,可以得到更低阶的滤波器。这对减少处理器的运算量、提高滤波器的实时性是非常重要的。最佳方法设计滤波器的一般步骤如下:

①根据实际项目要求确定滤波器的技术规范,例如截止频率、通带波纹等;

②根据滤波器的技术规范,估算所需的滤波器长度N值;

③使用最佳方法设计滤波器,并通过Matlab计算滤波器系数;

④通过Matlab仿真,检查设计的滤波器是否符合期望的技术规范。

2.2 滤波器技术规范的确定

图1是一个典型电阻抗成像硬件系统的部分结构框图。以此为例,详细地介绍使用最佳方法设计FIR滤波器的过程。

图1 电阻抗成像硬件系统部分结构框图

系统使用25 kHz的激励信号,电极对上的差分信号经过调理后送入模拟器件构成的相敏解调电路。解调得到的信号主要包含50 kHz的谐波信号和一个直流分量,其中直流分量是成像需要的数据。基于ARM处理器的FIR低通滤波器用于滤去50 kHz的谐波信号和其他干扰信号,获得成像所需的直流分量。根据采样定理,要正确识别50 kHz的信号,A/D转换器的采样率至少为100 ksps。为增强可靠性,滤波器使用150 kHz的抽样频率。经综合考虑,确定的滤波器技术规范如表1所列。

表1 FIR低通滤波器技术规范

2.3 估算满足技术规范要求所需的N值

对于FIR低通滤波器,滤波器长度 N可以由下面的经验公式估算出来[2]:

其中,ΔF是用抽样频率归一化的过渡带宽,δP为通带误差,δS为阻带误差。利用Matlab的remezord函数可以使得计算简化,所使用的M文件如下所示:

根据表1所列的技术规范可计算出 N=87,该值通常比实际值要略小些,可以将估算出来的N值增加1或2。一般来说,N值越大,可以获得性能越好的滤波器,但是处理器的运算时间也就相应地变长。因此,必须在滤波器的运算时间和滤波器的技术规范之间进行折中处理,根据实际要求对N值进行调整。

2.4 Matlab仿真

利用Matlab的remezord函数和估算的滤波器长度N,以最佳方法设计滤波器。通过Matlab仿真得到的滤波器幅频特性如图2所示。

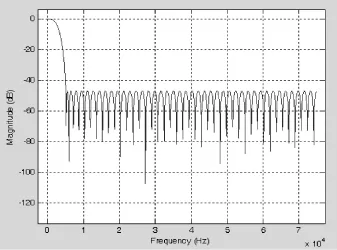
图2 最佳方法设计的滤波器幅频特性

从图2中可以看出,设计的滤波器通带为0～1 kHz,阻带衰减为46 dB,与表1所列技术规范基本相符。由此可见,使用最佳方法可以设计出能够很好地符合预期技术规范的滤波器。

3 FIR滤波器在ARM上的实现

3.1 Cortex-M3处理器简介[3]

ARM公司推出的Cortex-M3处理器具有如下特点:

◆采用哈佛结构,具有分支预测功能的三级流水线;

◆32位硬件除法和单周期乘法,在进行乘、乘加运算时已逼近DSP的性能;

◆具有很高的性价比和极低的功耗,能耗比达到0.06 mW/MHz;

◆具有丰富的片上资源,集成12位的A/D转换器、64 KB的RAM和512 KB的程序存储器。

因此,该处理器非常适合应用在电阻抗成像系统中。

3.2 滤波器系数的量化及其误差估计

从式(1)可知,FIR滤波器的实现就是滤波器的冲击响应系数与输入样本值的乘积和。使用最佳方法计算的滤波器系数都是非常精确的小数,为了提高定点ARM处理器的运算速度,需要将滤波器的系数转换为整数并使用有限的二进制位数表示。这就引入了系数量化误差,这种误差使得滤波器的频率响应偏离预期的响应。对于横向结构的FIR滤波器,在期望的误差范围内用多少位二进制数表示滤波器的系数,可以由式(5)估算[2]:

其中,E(ω)为期望的频响误差;N为滤波器长度;B表示滤波器系数的位数,值越大量化误差越小。对于使用量化后系数的滤波器,其阻带衰减 AMAX可由式(6)表示[2]:

为减小误差,同时避免运算过程的溢出,本文使用16位字长表示滤波器的系数。将B=16、N=87代入式(5)计算出E(ω)≈0.001,将 AS=0.1代入式(4)可得 δS≈0.005 6,将以上结果代入式(6)得到AMAX≈43.2 dB。与滤波器期望的45 dB相比,误差较小。因此,使用16位字长表示滤波器系数是有效的,能够满足系统要求。

3.3 滤波器的实现

滤波器的实现采用了批处理的方式,即先将数据采样放到内存中,数据采样完毕之后再对整个数据进行低通滤波。在Cortex-M3处理器中,式(1)中差分方程的计算将在32位累加器执行,利用调整指令序列的方法[4]可提高流水线的效率,充分发挥了ARM的32位内核优势。由于滤波器的系数比较多,采用汇编语言及块算法[5]编写滤波器程序,以提高程序的运行效率。块算法的核心是将装载进寄存器的数据反复使用,每次处理固定数目的数据块,极大地减少了比较耗时的数据装载和存储操作。本文使用4×4的块滤波器,根据算法要求,滤波器的系数和输出数据必须是4的倍数。为了验证滤波器工作的效果,假设相敏解调电路产生如下波形信号:

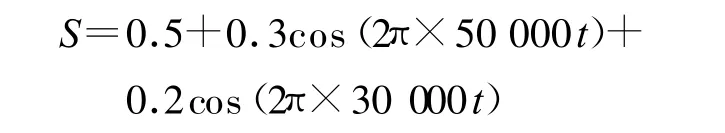
该信号包含0.5 V的直流信号、50 kHz的谐波信号和人为加入的30 kHz的干扰噪声,其波形如图3所示。

图3 滤波器的输入信号

模/数转换器以150 ksps的采样率对该波形取样,获取的数据存入数组中。在RealView MDK开发工具中编写程序并下载到ARM处理器中运行,将滤波器输出的信号通过串口传到PC机后,绘制的图形如图4所示。

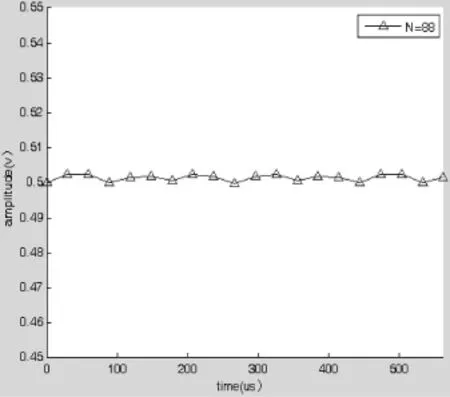
图4 滤波器的输出信号

由图4可见,设计的滤波器可以有效地滤除50 kHz的谐波信号和30 kHz的干扰信号,得到误差较小的直流分量,满足电阻抗成像系统的要求。具体数据如表2所列。

表2 滤波器的运行数据

结 语

FIR数字滤波器凭借优秀的性能,在数字信号处理的各个领域发挥着越来越重要的作用。本文介绍了使用最佳方法和Matlab设计FIR低通滤波器的方法,以及在ARM上的实现过程,为数字信号处理在嵌入式处理器上实现打下了良好基础。该滤波器应用于电阻抗成像系统中可以减小硬件电路开销,有效地提高系统的性价比。

[1]Brian Brown H.Medical impedance tomography and processimpedance tomography[J].Meas.Sci.Technol,2001,12(8).991-996.

[2]Emmanuel ifeachor C,Barrie Jervis W.数字信号处理实践方法[M].罗鹏飞,等译.2版.北京:电子工业出版社,2004.

[3]Joseph Yiu.ARM Cortex-M3权威指南[M].宋岩,译.北京:北京航空航天大学出版社,2009.

[4]邱铁,西方,迟宗正.ARM流水线关键技术分析与代码优化[J].单片机与嵌入式系统应用,2009(3):24-27.

[5]Andrew Sloss N,等.ARM嵌入式系统开发——软件设计与优化[M].沈建华,译.北京:北京航空航天大学出版社,2005.