一种点云数据获取的编码结构光方法研究

梁东魁

(燕山大学 信息科学与工程学院，河北 秦皇岛 066004)

在基于结构光的三维测量中，点云数据的精度和检测效率受到以下几方面的影响：摄像机观测条纹与投影仪模式之间的匹配算法的鲁棒性、边界点检测的准确性、三维坐标转换模型的精度等。解决匹配问题最有效的方法是对结构光进行编码，利用各种编码策略使像素本身带有先验编码信息，通过解码，实现光条或点的精确定位。因此，编码策略选择合适与否对匹配算法的复杂性和三维重建的准确性都有影响。目前，编码策略主要分为时间编码和空间邻域编码[1]。时间编码易于实现、空间分辨率高，但需要投射多幅结构光模式，不适用于运动物体的检测。空间邻域编码可以实现对动态物体的检测，但由于使用单一模式，空间分辨率较低，要求解码算法有较强的鲁棒性。两种编码策略各有特点，其中空间邻域编码策略更符合三维重建向并行化和动态实时发展的需求，在这一领域的研究也取得了一定成果。

[2]采用单帧等间距光栅投影，向被测物体投射等间距垂直黑白条纹。其优点在于投影光结构简单，数学模型明确，分析与误差检测方法成熟。但该方法的检测前提是图像条纹是连通的无宽度线，必须对原有的灰度图像进行阈值分割。而阈值分割方法会产生大量的条纹断裂现象，由于条纹标定基于条纹与基准条纹之间位置关系，如果其中线段有断裂，或者标定错误，都会扩散给所有条纹，对整体标定和计算检测都将产生很大的影响。参考文献[3]利用彩色空间红、绿、蓝三基色相互独立的特性，用彩色条纹对光栅进行编码。彩色编码条纹光栅采用4个条纹为一组，最少要有3个条纹才能确定其所在位置，如果被测物体的空间宽度容纳不下3个条纹，则无法进行测量，这是该方法对被测物体限制条件之一。

本文采用空间邻域编码思想，利用迪布鲁英序列(De Bruijn)对水平条纹进行编码。空间邻域编码只需要一种投射模式，利用局部邻域信息来生成码字，克服了等间距黑白条纹编码存在的不足。然而，空间邻域编码在某些情况下会丢失邻域信息，而使解码变得比较困难，影响到重建的精度。针对这一问题，本文提出了一种最优邻域匹配算法(BN-Matching)，对条纹边界进行全局最优解码，利用带有约束的动态编程(DP)技术[4]实现匹配过程。该算法在缺失部分邻域信息的情况下仍能有效进行解码。在检测条纹边界之前，对图像进行离线的颜色标定和预处理，进一步提高了检测的精度。

1结构光编码

本文采用4元3级De Bruijn序列对结构光进行水平等宽条纹编码。De Bruijn序列是一类最长的非线性反馈移位寄存器序列，可通过遍历De Bruijn图的欧拉回路或哈密尔顿回路获得[1]。n元m级序列的长度为nm，可表示为 d0，d1，…，dnm-1，其中 dj值取自 n 个基元，基元可以为任意数字或符号。序列中任意连续的m位组合在整个序列中都是唯一的，称为De Bruijn序列的窗口特性。在应用该序列进行结构光编码时，预先指定n种颜色，使其分别与 0，1，…，n-1 对应，将 0，1，…，n-1作为生成序列的基元，选择窗口大小为m，按照某一生成算法生成序列。例如，4元3级的De Bruijn序列如式1所示。若使 0、1、2、3分别对应一种特定的颜色，就可以生成一列宽为43=64的平行条纹结构光模式。

本方法通过升元算法[5]获得该序列，选择色调均匀分布的三原色及白色作为颜色元，所生成的结构光模式灰度图如图1所示。

图1 利用4元3级De Bruijn序列生成的结构光模式灰度图

本编码方案不要求序列中连续基元不同，为了降低检测条纹边界算法的复杂度，同时不增加颜色数，在生成光模式时，连续相同基元对应的条纹采用全照度与半照度相间的结构，例如，规定序列基元1对应颜色为红色，则子串 111 将采用(255，0，0)和(128，0，0)(色调值相同，但亮度值减半)间隔的结构，但在标识边界颜色码时仍按照4元模式处理，因此需要采集4元模式和相间模式两幅图。本编码方案要求物体表面在一个条纹宽度内变化平缓，不需要限制物体在全表面的单调性和连续性，因此本假定很易于实现。

2畸变条纹图像预处理

利用数字投影仪向物体表面投射图1所示的模式结构光，通过摄像机采集到经物体面形调制过的畸变条纹图像，由于受到物体表面反射特性、环境光以及投影仪和摄像机自身的色度亮度干扰等因素的影响，采集到的条纹图像颜色存在较大的偏差，影响到条纹边界颜色码的检测，有必要进行恰当的颜色校正。另外，可以通过图像处理进一步去除噪声。

2.1颜色标定

根据Caspi等[6]人提出的结构光系统照度模型，如式(1)所示，摄像机观测到的图像像素点的颜色向量S由以下几个因素决定：投影仪投射的结构光颜色P、被测物体表面点的反射矩阵K和摄像机所观测到物体环境光C0以及摄像机和投影仪本身色度亮度干扰矩阵A。

若要依次计算出 A、K、P、C0，需要额外的辅助设备和大量的处理时间，降低了实际操作的效率。另外，按照后续算法的要求，只需要实现近似的颜色校正。因此，实验选择在无外界光源的黑室中进行，忽略物体表面的反射性质(此时，造成颜色偏差的主要因素来自摄像机和投影仪本身色度亮度的干扰)，可以通过一个线性程序获得A。

首先，在采集畸变条纹图像之前，分别向一块白色平板上投射红、绿、蓝三种光，采集到三幅图像；在每幅图上采集一定数量的点，分别计算其红绿蓝三颜色通道的平均值，构成矩阵如下：

然后求出A-1，在对采集图像进行灰度化处理之前，使A-1左乘图像像素点颜色向量S，对颜色进行校正。

2.2灰度级处理

首先将经过校正的图像由位真彩色图转换为位灰度图，利用Robert算子进行条纹边界检测；然后采用高斯模板进行平滑去噪。为避免遗失某些边界信息，应设定一个较小的阈值，对图像进行区域分割，剔除背景；最后对二值图像进行形态学细化操作，得到单像素的条纹边界。此时，图像边界中包含物体的真实外轮廓边界，设定条件，去除真实外轮廓边界。图像预处理过程如图2所示。

图2 图像预处理过程

2.3生成边界集

3边界匹配

获得畸变条纹边界点的图像坐标数据和检测码后，必须对检测码进行解码。解码过程，即是解决摄像机观测条纹与投影仪投射模式条纹之间的匹配问题的过程。本文提出的BN-Matching算法，基于全局优化的思想，利用空间邻域信息对条纹边界进行最优匹配，并采用增加一定约束的动态编程的处理方法实现该算法。

3.1最优邻域匹配算法(BN-Matching)

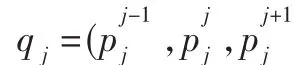
假设源边界Q与检测边界E之间的全局最优匹配为：Optm={(j0，i0)，(j1，i1)，…，(jK-1，iK-1)}，其中 j0≺ j1≺…≺jK-1，而 i0≺i1≺…≺iK-1。定义函数 agree(qj，ei)来评价 qj和 ei的匹配相似程度，则全局优化函数就可以表示为：

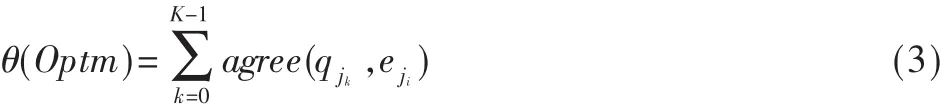
最优解为：

其中：

应用全局最优的思想进行解码，具有较强的抗噪能力，适用于所有采用De Bruijn序列对单一轴编码的结构光模式的解码。可以利用动态编程[4，6]思想进行最优匹配路径搜索。

3.2基于动态编程(DP)实现BN-Matching匹配

动态编程处理方法在双目立体视觉匹配研究中有广泛应用[5]，其思想是：首先迭代生成匹配代价矩阵Cost=[cji]，其元素如方程(5)所示；然后通过逆遍历代价矩阵得到最优匹配码。

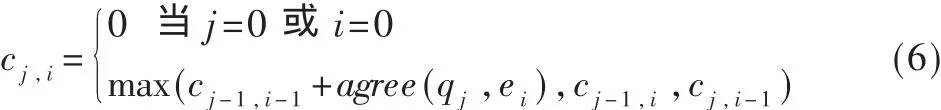
在边界检测过程生成的边界集E中，各条纹边界不要求邻接，但是按照顺序得到。根据此特点，在DP处理过程中增加适当的约束，计算生成最优匹配路径网格(BMPGrid)如图 3所示。

图3 最优匹配路径网格BMPGrid

成功完成边界匹配之后，同一边界像素点就带有了唯一的码字。根据光学三角测量原理，建立起系统空间数学模型，在点的码字与三维坐标之间建立直接对应关系，通过矩阵计算得到点的三维坐标，为进一步的三维表面重建和拼接提供点云数据。

4仿真实验

以VC++6.0作为编程工具，完成算法实现，以多种物体为模型进行了仿真实验。为了减少环境光干扰，实验选择在无外界光源的黑室中进行，预先计算出摄像机和投影仪的色度亮度干扰矩阵A：

利用A对图像进行颜色校正，通过后续的处理检验该校正是否能够满足实验要求。

图2为得到二维边界点数据的图像预处理过程，从图2(c)中可以看出，采用传统处理方法所得到的数据有一定的边界点缺失，条纹多处发生断裂和交叠。图4(a)、图4(b)为利用等间距黑白条纹结构光模式得到的三维点云分布，从图中可以看出，由于图像处理过程中条纹发生断裂，使得无法得到点所在的正确条纹号，造成数据缺失，必然会影响到后续的三维网格化及表面重构。

但从图 4(c)、图 4(d)中可以看到，经过坐标变换后的三维点云数据完整，能够呈现出物体的原始面形，说明匹配算法具有较强的鲁棒性，能够实现对畸变条纹边界的正确解码。

图4 仿真实验模型及获取的点云数据分布

本文提出的结构光编码方案，利用De Bruijn序列的窗口特性，充分利用局部邻域信息，采用基于全局优化思想的BN-Matching算法进行解码，不需要假定物体全表面单调。当邻域信息缺失或误检时，仍能进行正确匹配。对噪声有很强的鲁棒性，DP处理方法保证了算法的有效实现，通过坐标变换获得的点云数据能够满足三维表面重建的要求。

参考文献

[1]SALVI J， PAGES J， BATLLE J.Pattern codification strategies in structured light systems[J].Pattern Recgonition，2004，37(4)：827-849.

[2]周德芳.基于面结构光投影法的三维物体形状检测与重构系统[D].南京：东南大学，2004.

[3]刘维一，王肇圻.彩色组合编码条纹光栅轮廓术[J].光学学报，2000，20(9)：1218-1222.

[4]ZHANG L， CURLESS B， SEITZ S M.Rapid shape acquisition using color structured light and multi-pass dynamic programming[C].Int.Symposium on 3D Data Processing Visualization and Transmission， Padova， Italy， 2002.

[5]朱士信.DeBruijn序列的升元算法 [J].电子科学学刊，2000，22(1)：68-72.

[6]CASPI D，KIRYATI N， SHAMIR J.Range imaging with adaptive color structured light[J].Pattern Analysis and Machine Intelligence， 1998，20(5)：470-480.